


人教A版(2019)高一数学必修第二册--正弦定理、余弦定理的综合应用-【课件】
展开
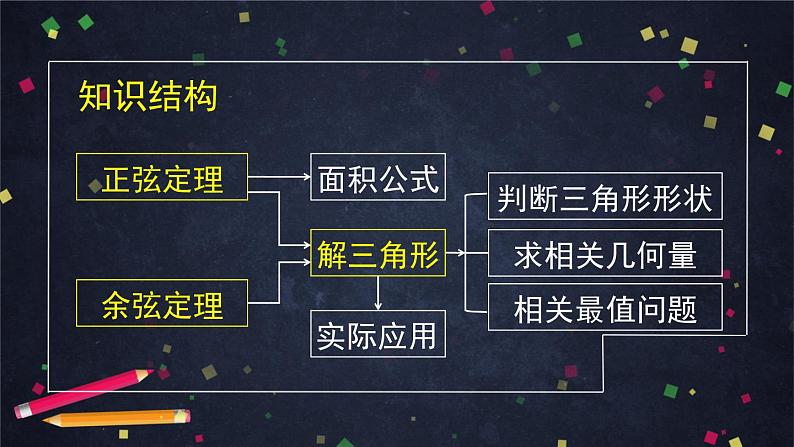
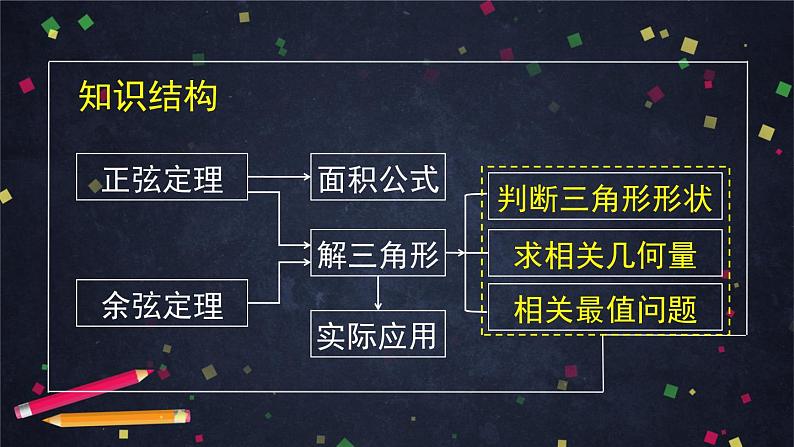
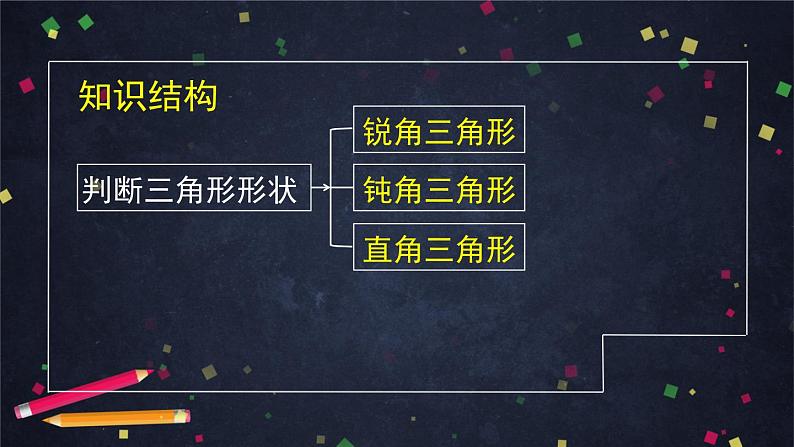
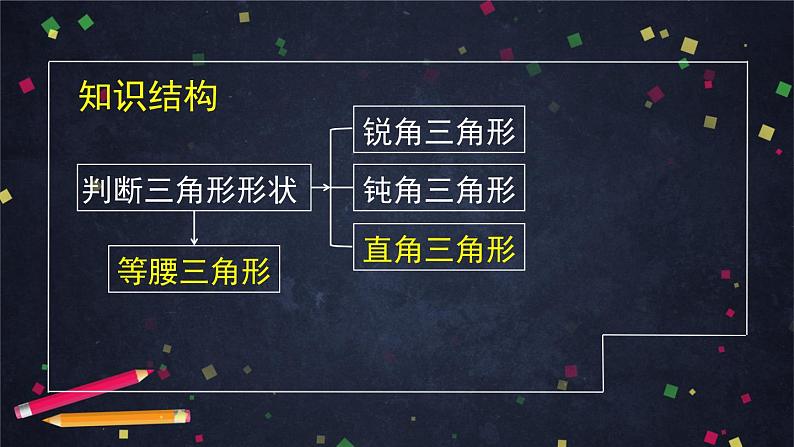
这是一份人教A版(2019)高一数学必修第二册--正弦定理、余弦定理的综合应用-【课件】,共60页。PPT课件主要包含了知识概要,面积公式,正弦定理,余弦定理,求相关几何量,解三角形,知识结构,实际应用,相关最值问题,判断三角形形状等内容,欢迎下载使用。
例:在△ 中,已知 , ,判断△ 的形状.
例:在△ 中,已知 , ,判断△ 的形状. 【分析】
例:在△ 中,已知 , ,判断△ 的形状. 【解答】
例:在△ 中,已知 , ,判断△ 的形状. 【解答】由正弦定理得 ,
例:在△ 中,已知 , ,判断△ 的形状. 【解答】由正弦定理得 ,又 , 所以 .可得 .
例:在△ 中,已知 , ,判断△ 的形状. 【解答】由正弦定理得 ,又 , 所以 .可得 .所以 .
例:在△ 中,已知 , ,判断△ 的形状. 【解答】由正弦定理得 ,又 , 所以 .可得 .所以 . 所以△ 为等边三角形.
例:在△ 中,已知 , 判断△ 的形状.
例:在△ 中,已知 , 判断△ 的形状. 【分析】
例:在△ 中,已知 , 判断△ 的形状. 【解答】
例:在△ 中,已知 , 判断△ 的形状. 【解答】由正弦定理得 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】由正弦定理得 . 所以 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】由正弦定理得 . 所以 . 所以 或 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】所以 ,或 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】所以 ,或 . 所以△ 为等腰或直角三角形.
例:在△ 中,已知 , 判断△ 的形状. 【解答】由余弦定理得 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】由余弦定理得 . 化简得 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】分解得 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】分解得 . 进一步分解得 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】分解得 . 进一步分解得 . 所以 或 .
例:在△ 中,已知 , 判断△ 的形状. 【解答】当 时,即 , 此时△ 为等腰三角形.
例:在△ 中,已知 , 判断△ 的形状. 【解答】当 时,即 , 此时△ 为直角三角形.
例:在△ 中,已知 , 判断△ 的形状. 【解答】当 时,即 , 此时△ 为直角三角形. 所以△ 为等腰或直角三角形.
例:在△ 中,已知 , , 判断△ 的形状.
例:在△ 中,已知 , , 判断△ 的形状. 【分析】
例:在△ 中,已知 , , 判断△ 的形状. 【解答】
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 所以 .即 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 所以 .即 . 因为 ,所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 所以 .即 . 因为 ,所以 .即 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 因为 ,所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 因为 ,所以 .所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 因为 ,所以 .所以 . 所以△ 为等腰直角三角形.
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 所以 . 所以 .所以 .
例:在△ 中,已知 , , 判断△ 的形状. 【解答】因为 ,所以 . 所以 . 所以 .所以 . 所以△ 为等腰直角三角形.
例:在△ 中,已知 , , ,求△ 的面积.
例:在△ 中,已知 , , ,求△ 的面积. 【分析】
例:在△ 中,已知 , , ,求△ 的面积. 【解答】
例:在△ 中,已知 , , ,求△ 的面积. 【解答】由正弦定理可得 . 所以 .所以 或 . 即 或 为直角.
例:在△ 中,已知 , , ,求△ 的面积. 【解答】因为 ,所以 不是直角. 所以 .所以 . 由余弦定理得 .
例:在△ 中,已知 , , ,求△ 的面积. 【解答】所以 .
例:在△ 中,已知 , , ,求△ 的面积. 【解答】所以 . 因为 ,所以 . 所以 .
例:在△ 中,已知 , , ,求△ 的面积. 【解答】因为 , 所以 .
例:在△ 中,已知 , , ,求△ 的面积. 【解答】因为 , 所以 . 因为 ,所以 不是直角.
例:在△ 中,已知 , , ,求△ 的面积. 【解答】所以 .即 . 由余弦定理得 . 所以 .
例:在△ 中,已知 , , ,求△ 的面积. 【解答】因为 ,所以 . 所以 .
例:在△ 中,已知 ,面积 , ,求△ 的周长.
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【分析】
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【分析】
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【解答】
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【解答】由正弦定理可得 . 即 .
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【解答】所以 .即 .
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【解答】
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【解答】所以 .即 . 所以 .
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【解答】所以 .即 . 所以 .因为 , 所以 .
例:在△ 中,已知 ,面积 , ,求△ 的周长. 【解答】由余弦定理 , 可得 . 解得 .所以周长为 .
例:在△ 中, , ,求△ 周长的最大值.
例:在△ 中, , ,求△ 周长的最大值.【分析】
例:在△ 中, , ,求△ 周长的最大值.【解答】由余弦定理 , 可得 .
例:在△ 中, , ,求△ 周长的最大值.【解答】由余弦定理 , 可得 .所以 .
例:在△ 中, , ,求△ 周长的最大值.【解答】由余弦定理 , 可得 .所以 . 由基本不等式得 .
例:在△ 中, , ,求△ 周长的最大值.【解答】即 ,所以 .
例:在△ 中, , ,求△ 周长的最大值.【解答】即 ,所以 . 可以知道 时,不等式取等号.
例:在△ 中, , ,求△ 周长的最大值.【解答】即 ,所以 . 可以知道 时,不等式取等号. 所以△ 周长的最大值为 .
例:在△ 中,已知 , ,求△ 面积的最大值.
例:在△ 中,已知 , ,求△ 面积的最大值. 【分析】
例:在△ 中,已知 , ,求△ 面积的最大值. 【分析】由正弦定理和余弦定理得 .整理得 .
例:在△ 中,已知 , ,求△ 面积的最大值. 【解答】由正弦定理和余弦定理得 .整理得 . 因为 ,所以 , .
例:在△ 中,已知 , ,求△ 面积的最大值. 【解答】所以 .
例:在△ 中,已知 , ,求△ 面积的最大值. 【解答】所以 . 由基本不等式得 .
例:在△ 中,已知 , ,求△ 面积的最大值. 【解答】可以知道 时不等式取等号. 此时 . 所以 .
例:在△ 中,已知 , ,求△ 面积的最大值. 【解答】可以知道 时不等式取等号. 此时 . 所以 .所以 .
例:在△ 中,已知 , ,求△ 面积的最大值. 【解答】可以知道 时不等式取等号. 此时 . 所以 .所以 . 所以面积 .
课堂小结
相关课件
这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用获奖课件ppt,共28页。PPT课件主要包含了正弦定理等内容,欢迎下载使用。
这是一份高中数学人教A版 (2019)必修 第二册6.4 平面向量的应用精品课件ppt,共20页。
这是一份高中人教A版 (2019)6.4 平面向量的应用公开课课件ppt,共23页。PPT课件主要包含了答案√√×,答案C等内容,欢迎下载使用。








