河北省沧州市献县2023-2024学年七年级下学期期中考试数学试卷(含答案)

这是一份河北省沧州市献县2023-2024学年七年级下学期期中考试数学试卷(含答案)，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
（考试时间：120分钟，满分：120分）
卷Ⅰ（选择题，共36分）
一、选择题（本大题共12个小题，每小题3分，共36分，在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 下列实数中：，，，，，无理数的个数有（ ）
A. 2个B. 3个C. 4个D. 5个
答案：A
2. 若，则点在（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
答案：B
3. 下列说法正确的是（ ）．
A. 的平方根是B. 的算术平方根是
C. 负数没有立方根D. 是2的算术平方根
答案：D
4. 在平面直角坐标系中，将点向上平移2个单位长度，得到点，则点的坐标是（ ）
A B. C. D.
答案：C
5. 下列命题是假命题的是（ ）
A. 同位角相等，两直线平行
B. 两条直线被第三条直线所截，内错角相等
C. 平行于同一条直线的两条直线平行
D. 任何数的立方根都只有一个
答案：B
6. 在平面直角坐标系的第四象限内有一点，到轴的距离为4，到轴的距离为6，则点的坐标为（ ）
A. B. C. D.
答案：D
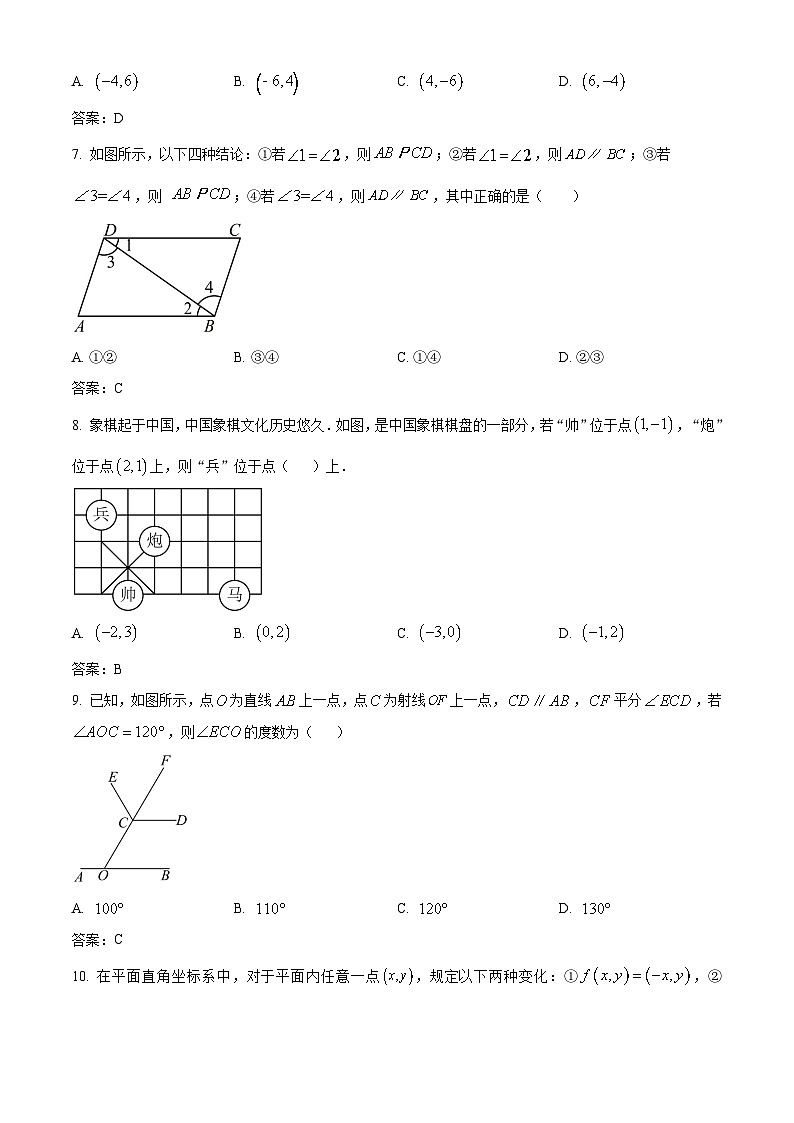
7. 如图所示，以下四种结论：①若，则；②若，则；③若，则 ；④若，则，其中正确的是（ ）
A. ①②B. ③④C. ①④D. ②③
答案：C
8. 象棋起于中国，中国象棋文化历史悠久．如图，是中国象棋棋盘的一部分，若“帅”位于点，“炮”位于点上，则“兵”位于点（ ）上．
A. B. C. D.
答案：B
9. 已知，如图所示，点为直线上一点，点为射线上一点，，平分，若，则的度数为（ ）
A. B. C. D.
答案：C
10. 在平面直角坐标系中，对于平面内任意一点，规定以下两种变化：①，②．按照该规定：（ ）．
A. B. C. D.
答案：A
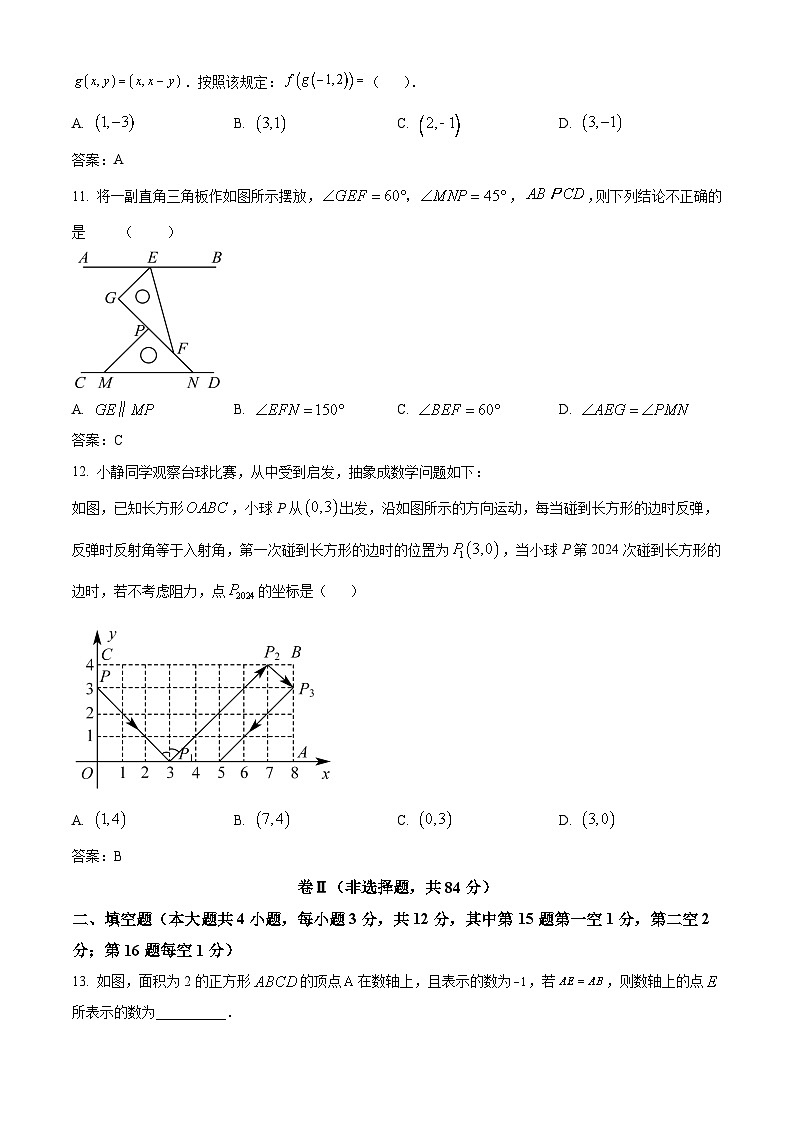
11. 将一副直角三角板作如图所示摆放，，，则下列结论不正确的是 （ ）
A. B. C. D.
答案：C
12. 小静同学观察台球比赛，从中受到启发，抽象成数学问题如下：
如图，已知长方形，小球P从出发，沿如图所示的方向运动，每当碰到长方形的边时反弹，反弹时反射角等于入射角，第一次碰到长方形的边时的位置为，当小球P第2024次碰到长方形的边时，若不考虑阻力，点的坐标是（ ）
A. B. C. D.
答案：B
卷Ⅱ（非选择题，共84分）
二、填空题（本大题共4小题，每小题3分，共12分，其中第15题第一空1分，第二空2分；第16题每空1分）
13. 如图，面积为2的正方形的顶点在数轴上，且表示的数为，若，则数轴上的点所表示的数为__________．
答案：##
14. 如图，将直角沿边的方向平移到的位置，连结，若，则的长为______．
答案：2
15. 如图，直线，相交于点，过点作，射线平分，，则的度数为________，的度数为________．
答案： ①. ##50度 ②. ##40度
16. 如图，四边形是长方形，点，分别在边和上，，，，．
（1）________，________；
（2）当的面积为26时，点的坐标为________．
答案： ①. ②. 6 ③.
三、解答题（本大题共8个小题，共72分．解答应写出文字说明、证明过程或演算步骤）
17. 已知某正数的两个平方根，它们分别是和的立方根是，求的算术平方根．
答案：3
解：由题意得：，
解得：，
又，
，
算术平方根为3．
18. 求下列各式中的值：
（1）；
（2）．
答案：（1）或
（2）
【小问1详解】
，
，
，
∴或；
【小问2详解】
，
，
，
∴．
19. 在平面直角坐标系中，已知点．
（1）若点M在x轴上，求m的值；
（2）若点，且直线轴，求线段的长．
答案：（1）
（2）6
【小问1详解】
∵点M在x轴上，
∴，
解得．
【小问2详解】
∵点，且直线轴，
∴，
解得．
故，
∴线段的长为．
20. 如图，在边长为1个单位长度的小正方形网格中建立平面直角坐标系，将三角形向右平移5个单位长度，再向上平移3个单位长度，请回答下列问题：
（1）画出平移后三角形，并写出三角形顶点的坐标；
（2）求三角形的面积．
答案：（1）见解析，，，
（2）
【小问1详解】
解：所画图形如下，其中的坐标为，的坐标为，的坐标为；
【小问2详解】
．
21. 如图，已知：中，D、E、F、G分别在、和上，连接、和，，．
（1）判断与的位置关系，并证明；
（2）若，，求的度数．
答案：（1），理由见详解；
（2）；
【小问1详解】
解：，理由如下：
∵，
∴，
∴，
又∵，
∴，
∴；
【小问2详解】
解：由（1）可知，，，
∵，
∴，
∵，
∴，
∵，
∴，
∴．
22. 我们知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，而，于是可用来表示的小数部分，根据以上信息回答下列问题：
（1）的小数部分为______，的小数部分为______；
（2）若m是的整数部分，n是小数部分，求的值．
答案：（1）；
（2）
【小问1详解】
解：∵，
∴的小数部分为；
∵，
∴，
∴，
∴小数部分为；
故答案为：，；
【小问2详解】
∵，m是的整数部分，
∴．
∵，n是的小数部分，
∴，
∴．
23. 已知当m，n都是实数，且满足时，称为“好点”．
（1）判断点，是否为“好点”，并说明理由；
（2）若点是“好点”，请判断点M在第几象限？并说明理由．
答案：（1）是“好点”，不是“好点”，理由见解析
（2）第三象限，理由见解析
【小问1详解】
解：是“好点”，不是“好点”，理由如下：由题意知，当时，
解得，，
∵，
∴，
∴是“好点”，
当时，
解得，，
∵，
∴，
∴不是“好点”；
【小问2详解】
解：第三象限，理由如下：
当时，
解得，，
∵点是“好点”，
∴，
解得，，
∴，
∴在第三象限．
24. 将三角板与三角板摆放在一起，与重合（如图1），，，．固定三角板不动，将三角板绕点顺时针旋转后停止，设旋转得．
（1）当边落在内时（如图2），求的度数；
（2）设三角板绕点旋转的速度为每秒5度，旋转时间为．若的一边与三角板的某边平行（不包含重合情况），请写出所有符合条件的的值．
答案：（1）
（2）15秒或24秒或27秒或33秒
【小问1详解】
解： ，
，
，
即的度数为；
【小问2详解】
解：如图1，当时，，
（秒）；
如图2，当 时，，
（秒）；
如图3，当时，，
（秒）；
如图4，当时，，
（秒）；
如图5，当时，，
（秒）；
综上可知，所有符合条件的的值为15秒或24秒或27秒或33秒．