







所属成套资源:【新教材大单元】人教版数学七年级下册课件+同步教案+导学案+同步练习+大单元教学设计
- 【新教材大单元】人教版数学七年级下册7.1.1 两条直线相交 课件+同步教案+导学案+同步练习 课件 3 次下载
- 【新教材大单元】人教版数学七年级下册7.2.1 平行线的概念(课件+同步教案+导学案+同步练习) 课件 2 次下载
- 【新教材大单元】人教版数学七年级下册7.1.3 两条直线被第三条直线所(课件+同步教案+导学案+同步练习) 课件 2 次下载
- 【新教材大单元】人教版数学七年级下册7.2.3 平行线的性质(第一课时)(课件+教案含反思+导学案+同步练习) 课件 1 次下载
- 【新教材大单元】人教版数学七年级下册7.2.3 平行线的性质(第二课时)(课件+教案含反思+导学案+同步练习) 课件 1 次下载
初中7.2.2 平行线的判定试讲课ppt课件
展开
这是一份初中7.2.2 平行线的判定试讲课ppt课件,文件包含722平行线的判定-课件pptx、722平行线的判定-教案docx、722平行线的判定-同步练习docx、722平行线的判定-同步探究学案docx等4份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
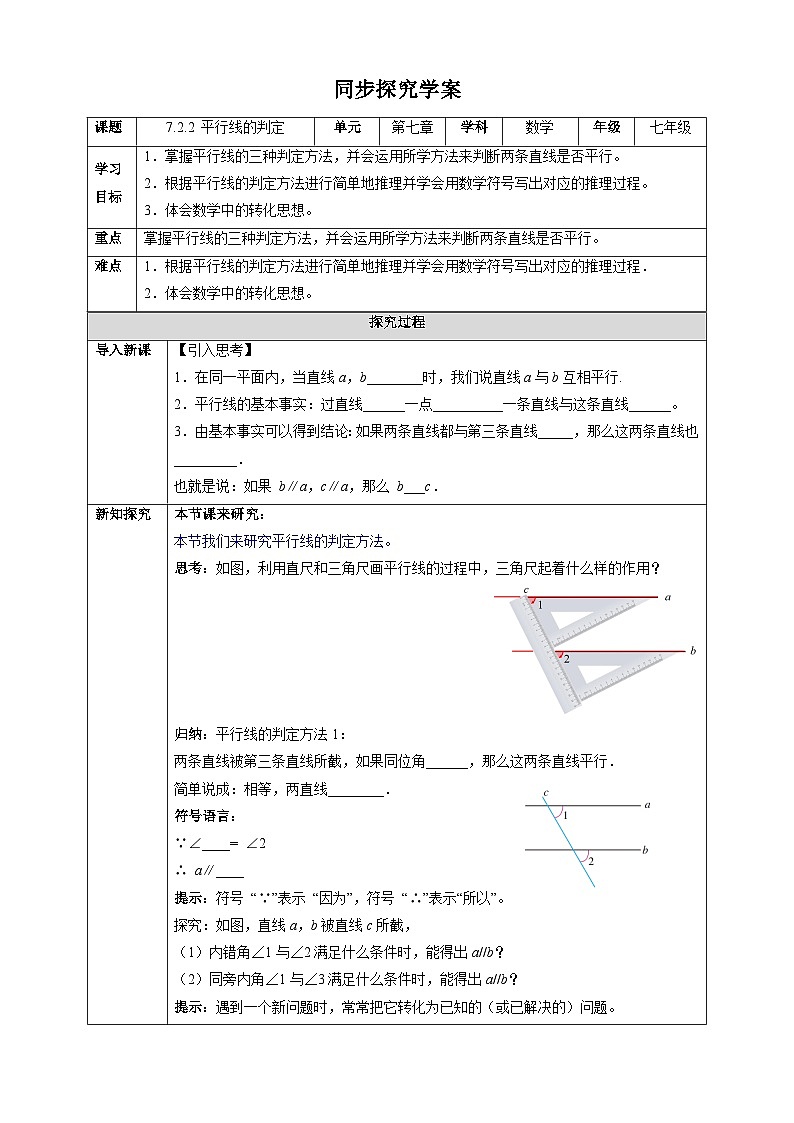
1.掌握平行线的三种判定方法,并会运用所学方法来判断两条直线是否平行。2.根据平行线的判定方法进行简单地推理并学会用数学符号写出对应的推理过程。3.体会数学中的转化思想。
1.在同一平面内,当直线a,b________时,我们说直线a与b互相平行.2.平行线的基本事实:过直线______一点__________一条直线与这条直线______。3.由基本事实可以得到结论:如果两条直线都与第三条直线_____,那么这两条直线也_________.也就是说:如果 b∥a,c∥a,那么 b___c.
我们已经知道,如果平面内的两条直线不相交,就可以判断这两条直线平行.但是,由于直线是无限延伸的,检验它们是否相交有困难,所以难以直接根据两条直线不相交来判断它们是否平行.那么,有没有其他判定方法呢?
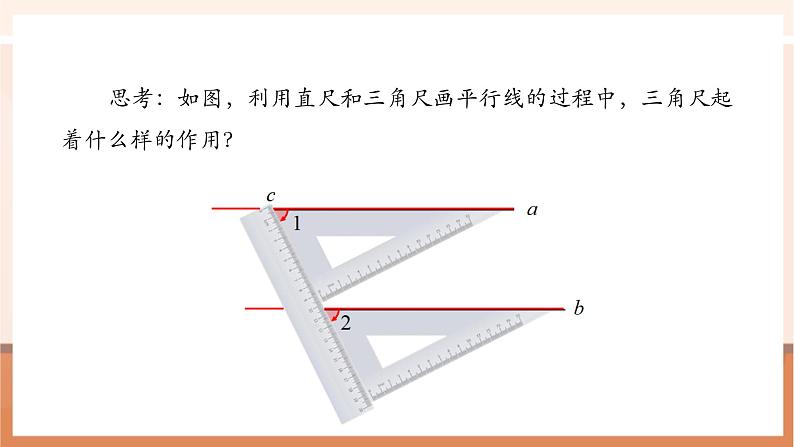
思考:如图,利用直尺和三角尺画平行线的过程中,三角尺起着什么样的作用?
将图简化,可以看出,画互相平行的直线a和b,实际上就是分别画相等的∠1和∠2的一条边,而∠1和∠2正是直线a,b被直线c截得的同位角.这说明,如果同位角∠1=∠2,那么a∥b.
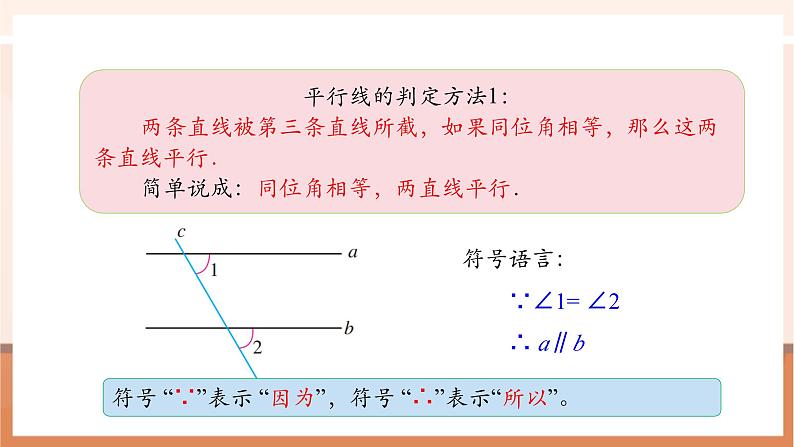
符号语言:∵∠1= ∠2∴ a∥b
平行线的判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.
符号 “∵”表示 “因为”,符号 “∴”表示“所以”。
观察下面的动图,进一步理解“同位角相等,两直线平行”.
探究:如图,直线a,b被直线c所截,
(1)内错角∠1与∠2满足什么条件时,能得出a//b?
解:如果∠1与∠2,由判定方法1,能得到a//b. 理由如下:∵∠1= ∠2(已知) ∠2= ∠4(对顶角相等)∴∠1=∠4(等量代换)∴a // b(同位角相等,两直线平行)
遇到一个新问题时,常常把它转化为已知的(或已解决的)问题。
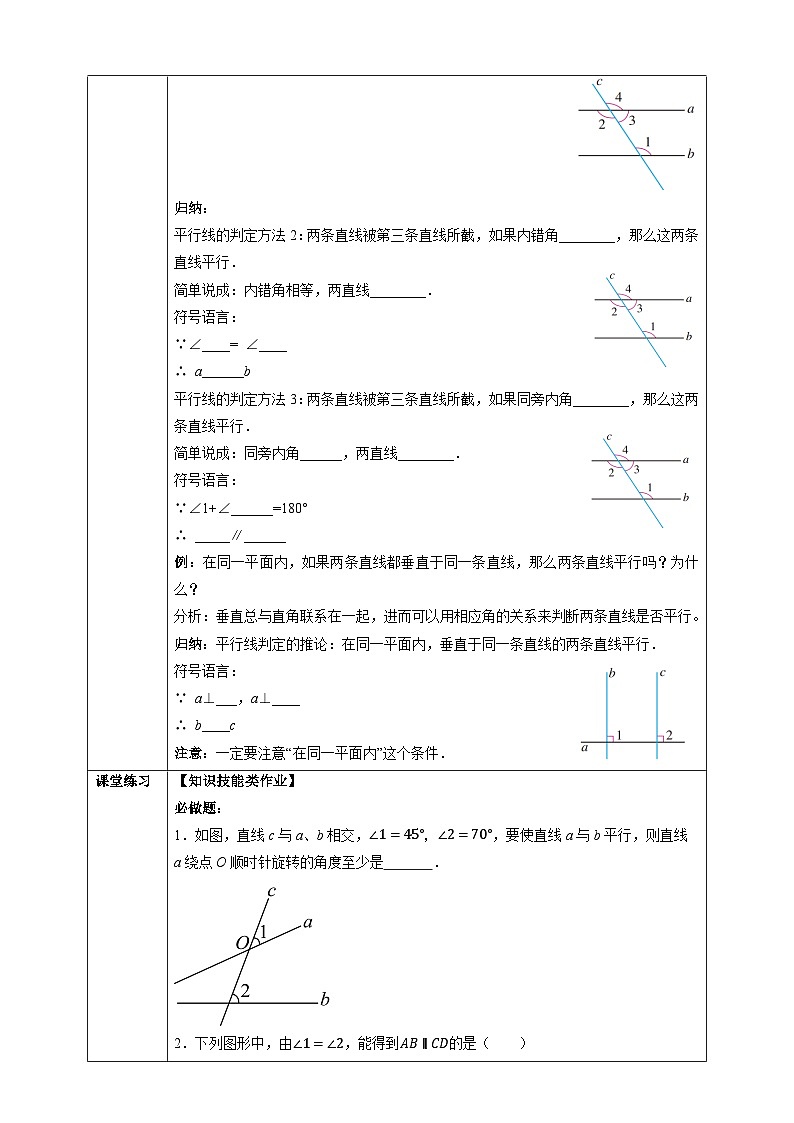
平行线的判定方法2:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.
观察下面的动图,进一步理解“内错角相等,两直线平行”.
(2)同旁内角∠1与∠3满足什么条件时,能得出a//b?
解:如果∠1+∠3=180° ,由判定方法1或方法2,能得到a//b. 理由如下:∵∠1+∠3=180° (已知) ∠4+∠3=180° (邻补角定义)∴∠1=∠4(等量代换)∴a∥b(同位角相等,两直线平行)
尝试一下,用判定方法2证明一下吧!
符号语言:∵∠1+∠3=180°∴ a∥b
平行线的判定方法3:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.
观察下面的动图,进一步理解“同旁内角互补,两直线平行”.
例:在同一平面内,如果两条直线都垂直于同一条直线,那么两条直线平行吗?为什么?
解:这两直线平行,理由如下:如图所示,∵ b⊥a(已知),∴ ∠1= 90°(垂直定义).同理∠2= 90°.∴ ∠1=∠2(等量代换).又 ∠1和∠2是同位角∴ b∥c(同位角相等,两直线平行)
分析:垂直总与直角联系在一起,进而可以用相应角的关系来判断两条直线是否平行。
你还能利用其他方法说明b∥c吗?
一定要注意“在同一平面内”这个条件.
符号语言:∵ a⊥b,a⊥c∴ b∥c
平行线判定的推论:在同一平面内,垂直于同一条直线的两条直线平行.
【知识技能类作业】必做题:
【知识技能类作业】选做题:
内错角相等,两直线平行
同位角相等,两直线平行
同旁内角互补,两直线平行
1.世界上最早记载潜望镜原理的古书,是公元前二世纪中国的《淮南万毕术》.书中记载了这样的一段话:“取大镜高悬,置水盘于其下,则见四邻矣”.现代潜艇潜望镜是在20世纪初发明的.如图是潜望镜工作原理的示意图,那么它所应用的数学原理是( ) A.内错角相等,两直线平行B.同旁内角互补,两直线平行C.对顶角相等D.两点确定一条直线
相关课件
这是一份初中数学人教版(2024)七年级下册(2024)7.4 平移精品课件ppt,文件包含74平移-课件pptx、74平移-教案docx、74平移-同步练习docx、74平移-同步探究学案docx等4份课件配套教学资源,其中PPT共27页, 欢迎下载使用。
这是一份数学七年级下册(2024)7.1.2 两条直线垂直优秀ppt课件,文件包含712两条直线垂直-课件pptx、712两条直线垂直-教案docx、712两条直线垂直-同步练习docx、712两条直线垂直-同步探究学案docx等4份课件配套教学资源,其中PPT共33页, 欢迎下载使用。
这是一份数学七年级下册(2024)第七章 相交线与平行线7.2 平行线7.2.1 平行线的概念获奖课件ppt,文件包含721平行线的概念-课件pptx、721平行线的概念-教案docx、721平行线的概念-同步练习docx、721平行线的概念-同步探究学案docx等4份课件配套教学资源,其中PPT共31页, 欢迎下载使用。










