北师大版（2024）七年级下册（2024）1 现实中的变量授课课件ppt

这是一份北师大版（2024）七年级下册（2024）1 现实中的变量授课课件ppt，共25页。PPT课件主要包含了开始制动，完全停止，自变量，因变量等内容，欢迎下载使用。
1. 在具体情境中理解什么是变量、自变量、因变量，并能举出反映变量之间关系的例子.
汽车刹车时，其制动装置开始发挥作用的瞬间车速称为制动初速度；汽车从开始制动到完全停止所驶过的距离称为制动距离.
汽车刹车时，其制动装置开始发挥作用的瞬间车速称为制动初速度；汽车从开始制动到完全停止所驶过的距离称为制动距离.思考 (1)这个情境中有哪些量?(1)制动初速度，制动距离.
知识点1 变量和常量
汽车刹车时，其制动装置开始发挥作用的瞬间车速称为制动初速度；汽车从开始制动到完全停止所驶过的距离称为制动距离.思考 (2)随着车辆制动初速度的变化，其他量会发生变化吗?(2)会.
(3)下表呈现了一辆汽车在某种路面情况下的部分刹车实验数据，你能描述制动距离随制动初速度的变化而变化的情况吗?
(3)制动距离随制动初速度的增大而增大.
探究 1.某海域海水的压强p(单位:Pa)与水深h(单位:m)之间的关系满足:p=9.8ρh(其中ρ为海水的密度，通常为1.03×103kg/m3).(1)这个情境中有哪些量?(2)随着水深h的变化，其他量会发生变化吗?(1)海水的压强p，水深h，海水的密度ρ.(2)随着水深h的变化，海水的压强p会发生变化，海水的密度ρ不会发生变化.
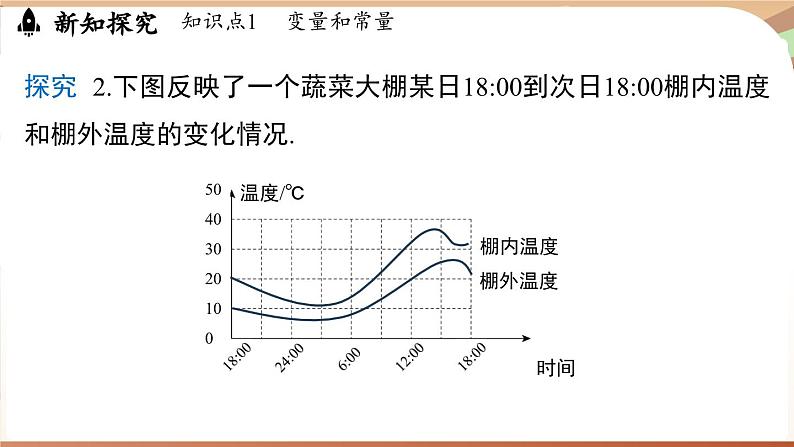
探究 2.下图反映了一个蔬菜大棚某日18:00到次日18:00棚内温度和棚外温度的变化情况.
(1)这个情境中有哪些量?(1)时间，棚内温度，棚外温度.
(2)你能描述这个蔬菜大棚棚内温度随时间的变化而变化的情况吗?棚外温度呢?
(2)这个蔬菜大棚棚内温度随时间的变化先降低后升高，再降低再升高.棚外温度随时间的变化先降低再升高再降低.
(3)你还有哪些发现?
(3)答案不唯一，这个蔬菜大棚某日18:00到次日18:00棚内温度一直比棚外温度高.
变量和常量:在变化过程中，数值发生变化的量称为变量，数值始终不变的量称为常量.
上面情境中有许多变化的量，如制动距离、制动初速度、海水的压强、水深、棚内温度、棚外温度、时间等，它们都是变量.你能举个常量的例子吗？
一定海域内，在海水的压强随水深变化而变化的过程中，海水的密度保持不变.像这种在变化过程中数值始终不变的量称为常量.
变量与常量是相对于某个变化过程而言的.当变化过程改变时，其中的变量与常量也可能随之改变.例如：对于s=vt，当v不变时，v为常量，s，t为变量；当t不变时，t为常量，s，v为变量.
例1 如图，把两根木条AB和AC的一端A用螺栓固定在一起，木条AB固定不动，木条AC自由转动至AC′的位置.在转动过程中，下面的量是常量的为( )A.∠BAC的度数 B.BC的长度C.△ABC的面积 D.AC的长度
解析:木条AC绕点A自由转动至AC′的过程中， ∠BAC的度数、BC的长度、△ABC的面积一直在变化，均是变量. AC的长度始终不变，故AC的长度是常量.
自变量和因变量:一般地，在某个变化过程中，如果有两个变量x，y，并且变量y随着变量x的变化而变化，那么我们就说x是自变量，y是因变量.
知识点2 自变量和因变量
回顾刚刚的问题，你能辨别其中的自变量和因变量吗？
上面情境中制动距离、制动初速度、海水的压强、水深、棚内温度、棚外温度、时间等变量.制动距离随制动初速度的变化而变化，海水的压强随水深的变化而变化，棚内温度、棚外温度随时间的变化而变化.
自变量与因变量的区别与联系
先发生变化或主动发生变化的量.
随着自变量的变化而变化的量.
①两者都是某一变化过程中的变量；②两者因研究的侧重点或先后顺序不同可以相互转化.
例2 下列情境中有哪些变量?其中，哪个是自变量，哪个是因变量?地表以下岩层的温度y(单位:℃)随所处深度x(单位:km)的变化而变化，在某地y与x之间的关系可以近似地表示为y=35x+20.
解:变量:地表以下岩层的温度y，所处深度x.其中，x是自变量，y是因变量.
跟踪训练 在利用太阳能热水器来加热水的过程中，热水器里的水温会随着太阳照射时间的长短而变化,在这个变化过程中,自变量是( )A.热水器里的水温B.太阳光的强弱C.热水器的容积D.太阳照射时间的长短
1.以固定的速度v0(米/秒)向上抛一个小球，小球的高度h(米)与小球运动的时间t(秒)之间的关系式是h=v0t-4.9t2，在这个关系式中，常量、变量分别为( )A.4.9是常量，t，h是变量 B.v0是常量，t，h是变量C.v0，-4.9是常量，t，h是变量 D.4.9是常量，v0，t，h是变量解析:h=v0t-4.9t2中的v0，-4.9是定值，故v0和-4.9是常量；t，h是变化的量，故t，h是变量.
2.下列情境中有哪些变量?其中，哪个是自变量，哪个是因变量?根据全国人口普查结果，1982-2020年全国总人口的变化情况如下(精确到 0.01 亿人):
答：变量:年份，人口.其中，年份是自变量，人口是因变量.
3.在某些情况下，可以按照体表面积计算用药剂量.有一种针对体重在30kg以下儿童的计算方法:儿童体表面积(单位:m2)=0.035×体重(单位:kg)+0.1某种药儿童用药剂量=该药成人用药剂量×儿童体表面积÷1.73.(1)这个情境中有哪些变量?变量之间有什么关系?
解:(1)变量:体重、儿童体表面积、某种药儿童用药剂量.变量之间的关系:体重增加时，儿童体表面积增加，某种药儿童用药剂量也增加.
(2)有一种药物，成人每次用药剂量为1g.按照上述方法，体重为15kg的儿童每次用药剂量大约是多少?
(2)因为儿童体表面积=0.035×15 +0.1=0.625(m2)，所以此种药儿童用药剂量=1×0.625÷1.73≈0.36(g).答:按照题中方法，体重为15kg的儿童每次用药剂量大约是0.36g.