浙教版（2024）九年级上册1.4 二次函数的应用优秀ppt课件

这是一份浙教版（2024）九年级上册1.4 二次函数的应用优秀ppt课件，共16页。PPT课件主要包含了齐声朗读，不等式是图像的一部分，水平线y2，水平线y-2，新知引入，新知讲解，当堂检测，配方变形或利用公式，其中0x2等内容，欢迎下载使用。
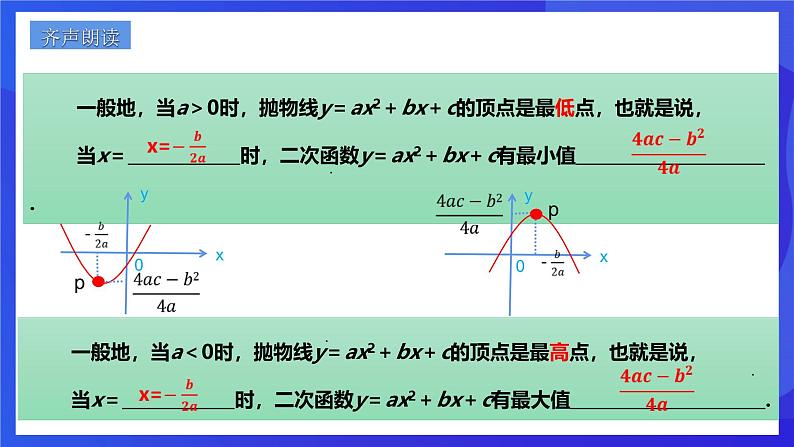
一般地，当a＞0时，抛物线y＝ax2＋bx＋c的顶点是最低点，也就是说，当x＝ 时，二次函数y＝ax2＋bx＋c有最小值 .
一般地，当a＜0时，抛物线y＝ax2＋bx＋c的顶点是最高点，也就是说，当x＝ 时，二次函数y＝ax2＋bx＋c有最大值 .
如图①中窗户边框的上部分是由4个全等扇形组成的半圆，下部分是矩形（如图②）.如果制作一个窗户边框的材料的总长度为6m，那么如何设计这个窗户边框的尺寸，使透光面积最大(结果精确到0.01m)?
运用二次函数求实际问题中的最大值或最小值，一般步骤：
①把问题归结为二次函数问题（设自变量和函数）；
②求出函数表达式和自变量的取值范围；
③通过配方变形或利用公式求它的最值（在自变量的取值范围内）；（或利用函数图象找最值）.
注意：求出的最大值或最小值对应的自变量的值必须在自变量的取值范围内.
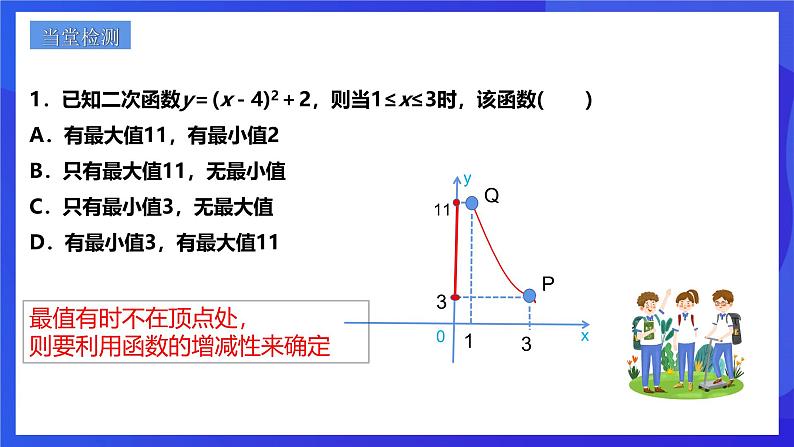
1．已知二次函数y＝(x－4)2＋2，则当1≤x≤3时，该函数( )A．有最大值11，有最小值2B．只有最大值11，无最小值C．只有最小值3，无最大值D．有最小值3，有最大值11
最值有时不在顶点处，则要利用函数的增减性来确定
解： ⑴配方得： y=(x－2)2＋3
又因为： a=1>0，则：图像开口向上，
所以：当x=2时，y 达到最小值为3
⑵ a=－5＜0，则：图像开口向下，函数有最大值
4.把一根长1m的铅丝折成一个矩形，并使矩形的面积最大，应怎样折？最大面积是多少？
解：设矩形的面积为y（m2), 矩形的一条边长为x(m)
a=－1＜0，图像开口向下，函数有最大值
5.用长为8米的铝合金制成如图窗框，问窗框的宽和高各多少米时，窗户的透光面积最大?最大面积是多少?
解：设矩形窗框的宽为x(m)，面积为y（m2),由题意得，
6.已知直角三角形的两直角边的和为2，求斜边长可能达到的最小值，以及当斜边长达到最小值时两条直角边的长．
解：设其中的一条直角边长为x，则另一条直角边长为（2-x），又设斜边长为y，
8.有一张边长为10cm的正三角形纸板，若要从中剪一个面积最大的矩形纸板，应怎样剪？最大面积为多少？