初中数学浙教版（2024）九年级上册3.4 圆心角精品课件ppt

这是一份初中数学浙教版（2024）九年级上册3.4 圆心角精品课件ppt，共22页。PPT课件主要包含了圆心角所对的弧相等，圆心角所对的弦相等，新知引入，∠AOB∠COD，ABCD，OEOF，等边三角形，圆的对称性，垂径定理及其逆定理，圆心角定理及其逆定理等内容，欢迎下载使用。
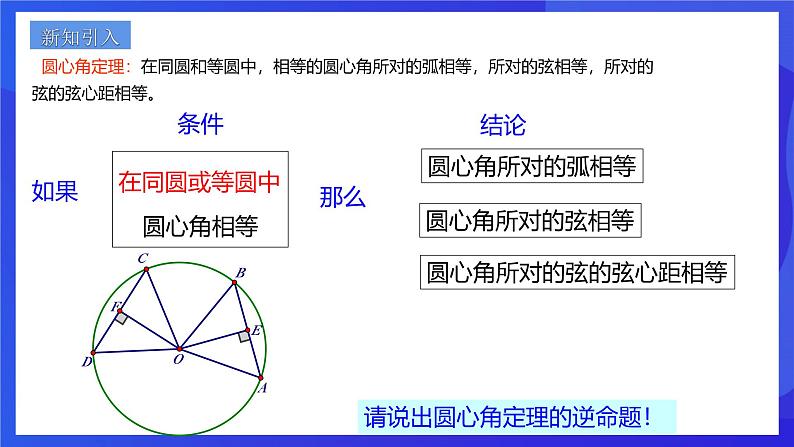
圆心角定理：在同圆和等圆中，相等的圆心角所对的弧相等，所对的弦相等，所对的弦的弦心距相等。
在同圆或等圆中圆心角相等
圆心角所对的弦的弦心距相等
请说出圆心角定理的逆命题！
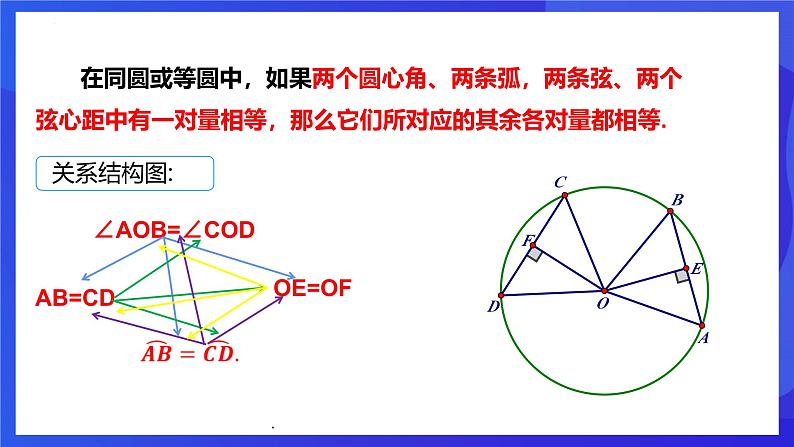
在同圆或等圆中，如果两个圆心角、两条弧，两条弦、两个弦心距中有一对量相等，那么它们所对应的其余各对量都相等.
1 如图，等边三角形ABC内接于⊙O，连结OA，OB，OC．
⑴ ∠AOB 、∠COB、 ∠AOC分别为多少度？
120（弦相等，则圆心角相等）
⑶判断四边形BDCO是哪一种特殊四边形，并说明理由。
菱形 OB=OC=BD=CD
⑷若⊙O的半径为r,求等边三角形ABC的边长？
⑸若等边三角形ABC的边长a,求⊙O的半径为多少？
(有一个角是600的等腰三角形是等边三角形）
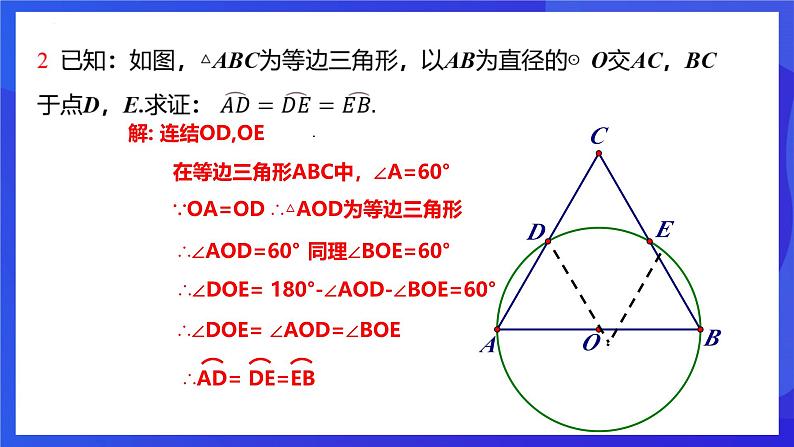
在等边三角形ABC中，∠A=60°
∴△AOD为等边三角形
∴∠DOE= 180°-∠AOD-∠BOE=60°
∴∠DOE= ∠AOD=∠BOE
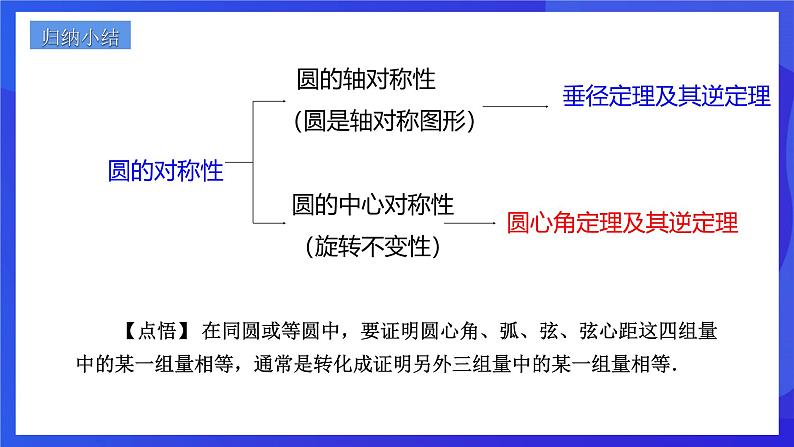
圆的轴对称性（圆是轴对称图形）
圆的中心对称性（旋转不变性）
【点悟】 在同圆或等圆中，要证明圆心角、弧、弦、弦心距这四组量中的某一组量相等，通常是转化成证明另外三组量中的某一组量相等．
2.如图，在直径为10cm的☉O中，直径AC与BD所在的角∠AOB=120°，求四边形ABCD的周长和面积.
在同圆中，相等的弦所对的弧相等
在同圆中，相等的弧所对的弦相等
变式训练：若AD=BC，那么比较AB与CD的大小.
6.下列命题是真命题的是（ ）（A）相等的圆心角所对的弧相等（B）长度相等的两条弧是等弧（C）等弦所对的圆心角相等（D）等弧所对的弦相等
7、如图4，AB是⊙O的直径，BC=CD=DE，∠COD=35°，求∠AOE的度数。
解： ∵ BC=CD=DE∴∠COB=∠COD=∠DOE=35°∴∠AOE=1800-∠COB-∠COD-∠DOE =750
9.　如图，AB，AC，BC都是⊙O的弦，且∠CAB＝∠CBA，求证：∠COB＝∠COA.
∴∠COB＝∠COA.
∵∠DAO= ∠EAO
(角平分線上的點到線段兩端的距離相等）
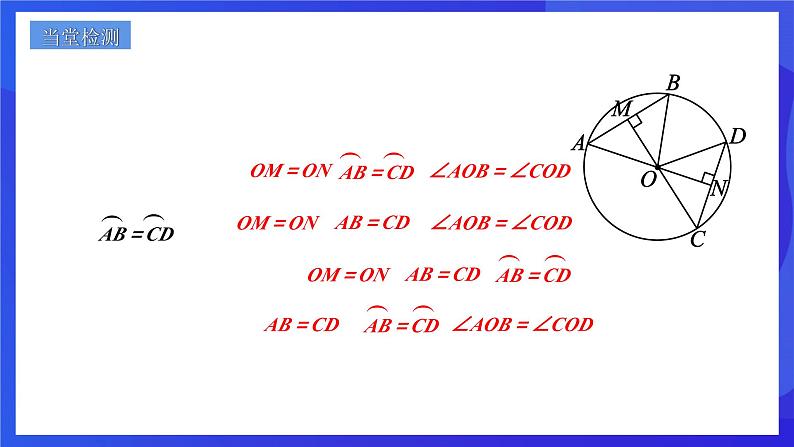
11.如图，已知点O是∠EPF 的平分线上一点，P点在圆外，以O为圆心的圆与∠EPF 的两边分别相交于A、B和C、D， 求证：AB=CD
分析： 联想到“角平分线的性质”，作弦心距OM、ON，
要证AB=CD ，只需证OM=ON.
如图，P点在圆内，AB=CD吗？
12、如图, AB、CD是⊙O的两条直径。
(1)顺次连结点A、C、B、D，所得的四边形是什么特殊四边形？为什么？
(2)四边形ACBD有可能为正方形吗？若有可能,当AB、CD有何位置关系时，四边形ACBD为正方形？为什么？
解：如图，所得的四边形是矩形，理由如下：
∵AC，BD是⊙O的直径
∴AO=OC=OB=OD
∴四边形ABCD是平行四边形
∴四边形ABCD是矩形
当AC⊥BD时，四边形ABCD是正方形
13．已知：如图，AB，CD是⊙O的两条弦，AB＝CD. 求证：∠OBA＝∠ODC.
证明：过点O分别作OE⊥AB于点E，OF⊥CD于点F.∵AB＝CD，∴OE＝OF.又∵BO＝DO，∴Rt△BOE≌Rt△DOF(HL)，∴∠OBA＝∠ODC.