浙教版（2024）九年级上册4.3 相似三角形完整版课件ppt

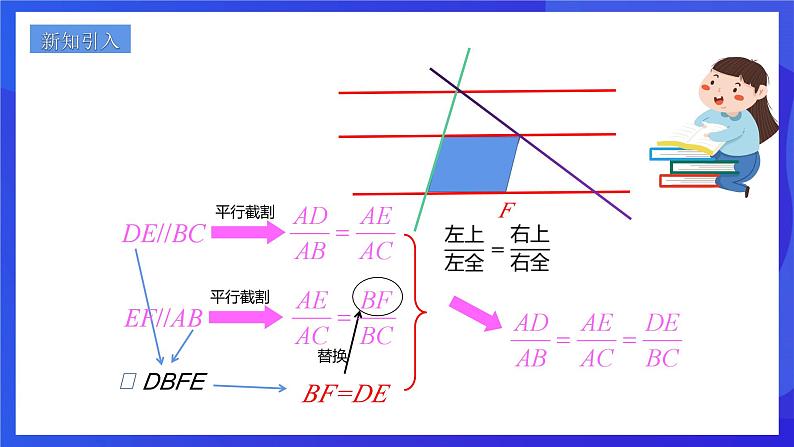
这是一份浙教版（2024）九年级上册4.3 相似三角形完整版课件ppt，共18页。PPT课件主要包含了BFDE，相似三角形的预备定理，几何语言叙述，“母子相似定理”等内容，欢迎下载使用。
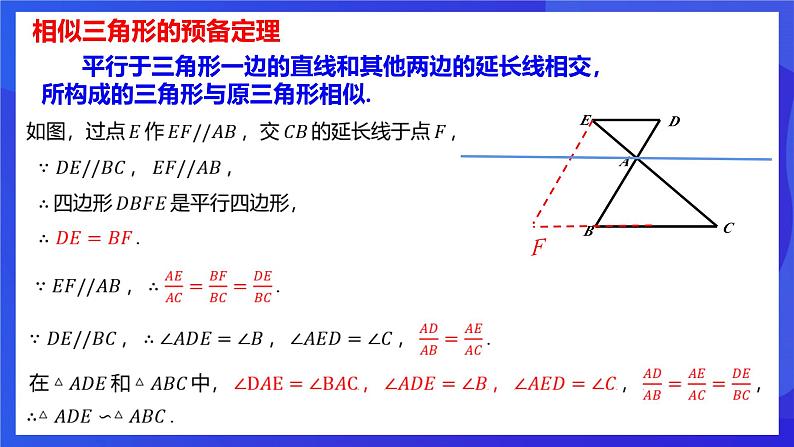
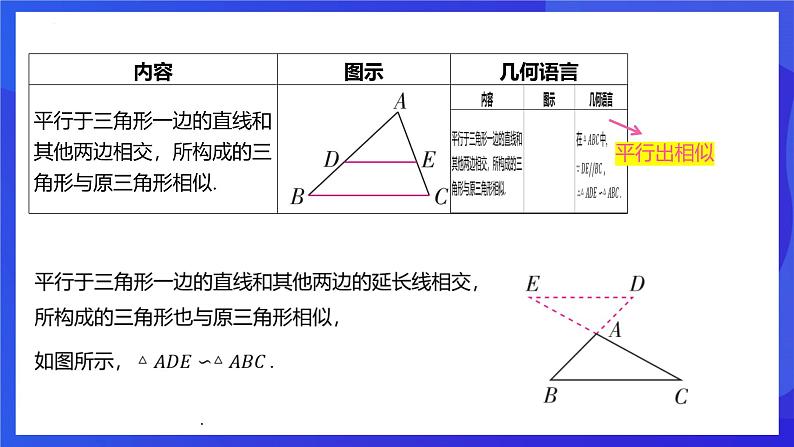
平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.
三角对应相等+三边对应成比例=相似三角形.
平行于三角形一边的直线和其他两边的延长线相交，所构成的三角形与原三角形相似.
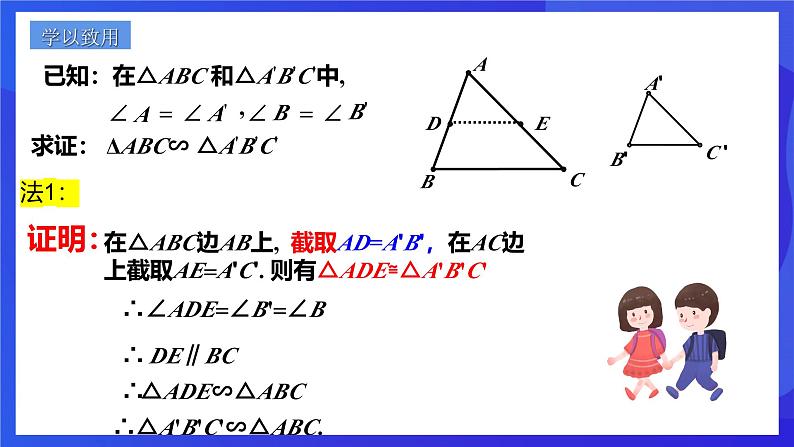
在△ABC边AB上, 截取AD=A'B'，在AC边上截取AE=A'C'. 则有△ADE≌△A'B'C'
∴∠ADE=∠B'=∠B
∴△A'B'C'∽△ABC.
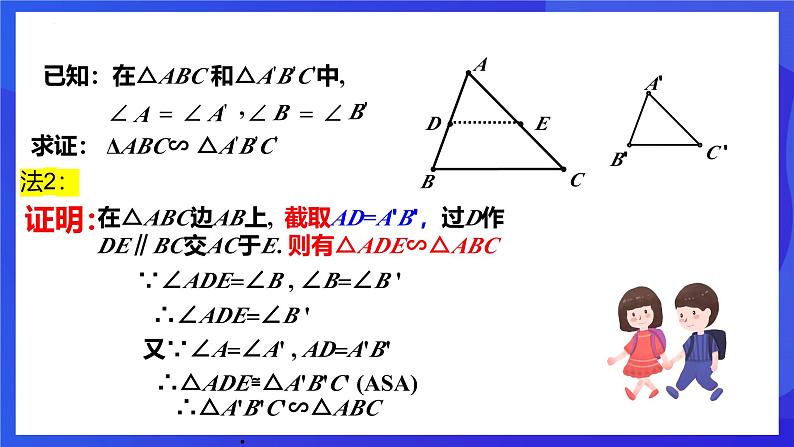
在△ABC边AB上, 截取AD=A'B'，过D作DE∥BC交AC于E. 则有△ADE∽△ABC
∵∠ADE=∠B , ∠B=∠B '
∴∠ADE=∠B '
又∵∠A=∠A' , AD=A'B'
∴△ADE≌△A'B'C' (ASA)
∴△A'B'C'∽△ABC.
判定定理1: 如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
两角对应相等,两三角形相似.
∵∠A=∠A´，∠B=∠B´
∴⊿ABC∽⊿A´B´C´
1.能否判定如图△ABC与△A′B′C′ 相似？为什么？
解：能判定这两个三角形相似，因为有两个角对应相等
2.如图, 已知DE∥BC , DF∥AC, 请尽可能多地找出图中的相似三角形，并说明理由.
△ABC∽△DBF∽△ADE.
3.已知：Rt△ABC中，∠ACB=90°，CD⊥AB 试写出图中的相似三角形.
证明：∵∠B=∠B，∠CDB=∠ACB=90°， ∴△ABC∽△CDB(两个角对应相等,两三角形相似). 同理可证：△ABC∽△ACD ∴△ABC∽△CBD∽△ACD.
直角三角形斜边上的高分成的两个直角三角形和原三角形相似。
4．如图，已知∠ACB＝∠CDB＝Rt∠．图中这两个三角形相似吗？如果你认为相似，请说明理由；如果你认为不一定相似，请添加一个条件，使这两个三角形一定相似．解：不一定相似．可以添加条件：∠ABC＝∠BCD，或∠ABC＝∠CBD，或∠A＝∠CBD，或∠A＝∠BCD，或AB∥CD等．
5．已知：如图，在☉O中，弦AB与弦CD交于点P．(1)求证：△ADP∽△CBP．(2)判断AP·BP＝DP·CP是否成立，并给出证明．
(1)证明：在△ADP和△CBP中，∠A＝∠C，∠D＝∠B，∴△ADP∽△CBP(2)成立∵△ADP∽△CBP，∴AP：CP＝DP：BP，∴AP·BP＝CP·DP．
6．如图，等腰三角形ABC的顶角∠A＝36°，BD是∠ABC的平分线．判断点D是不是线段AC的黄金分割点，并说明理由．
解：点D是线段AC的黄金分割点．理由如下：∵∠A＝36°，AB＝AC，∴∠ABC＝72°．∵BD平分∠ABC，∴∠DBC＝36°．∴∠DBC＝∠A，∵∠C＝∠C，∴△ABC∽△BCD．∴AC：BC＝BC：CD．而BC＝BD＝AD，所以点D是AC的黄金分割点．