浙教版数学九年级上册第四章《相似三角形章末复习------开心图形》 课件

这是一份浙教版数学九年级上册第四章《相似三角形章末复习------开心图形》 课件，共23页。
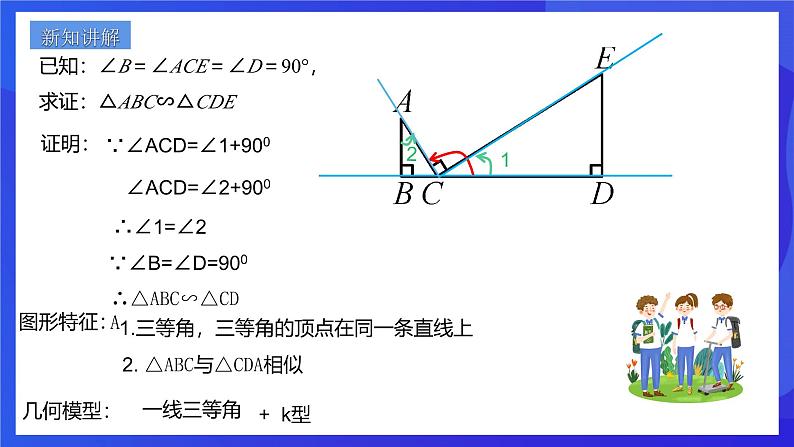
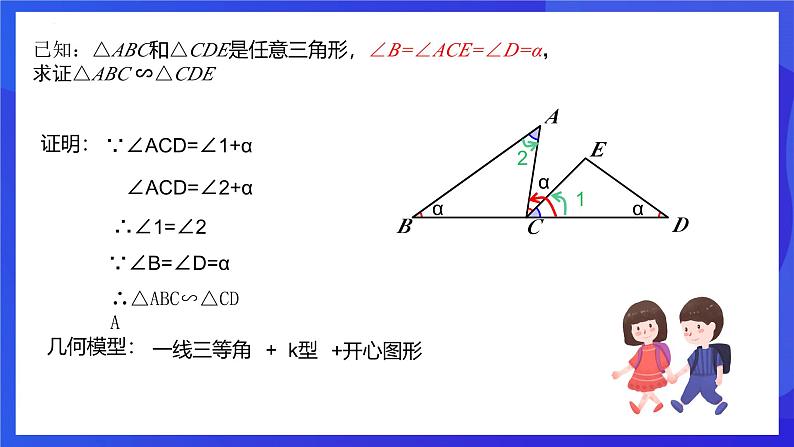
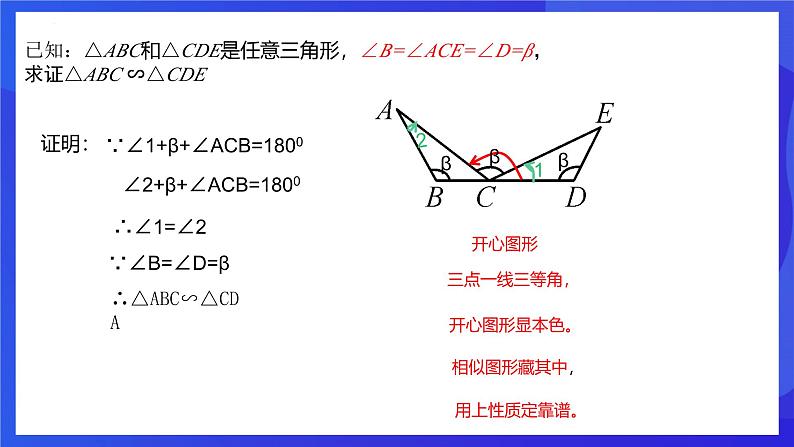
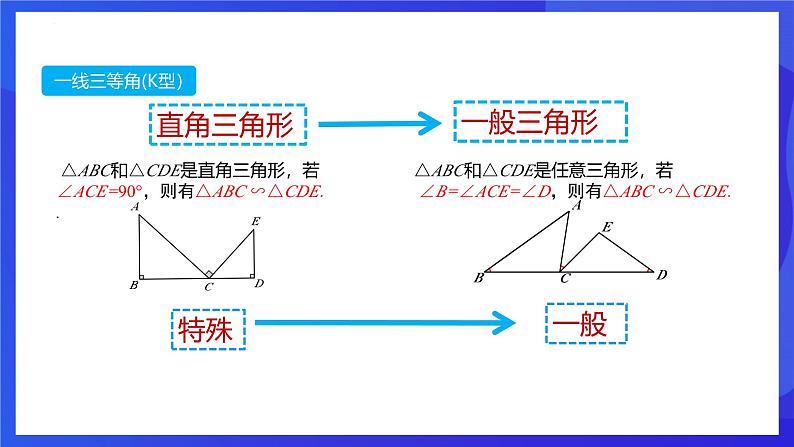
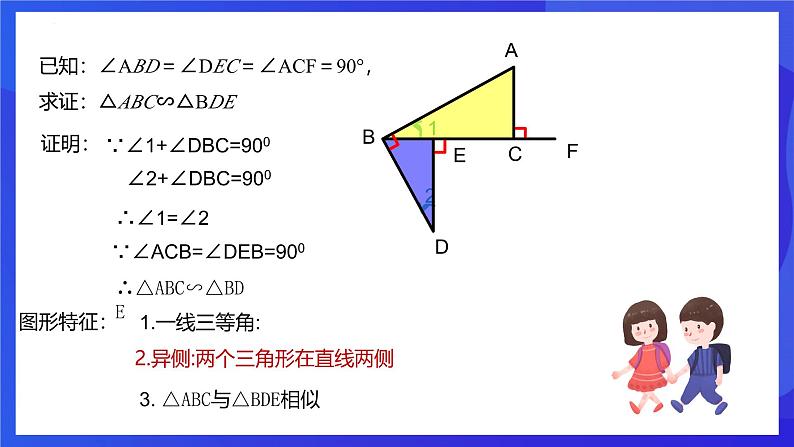
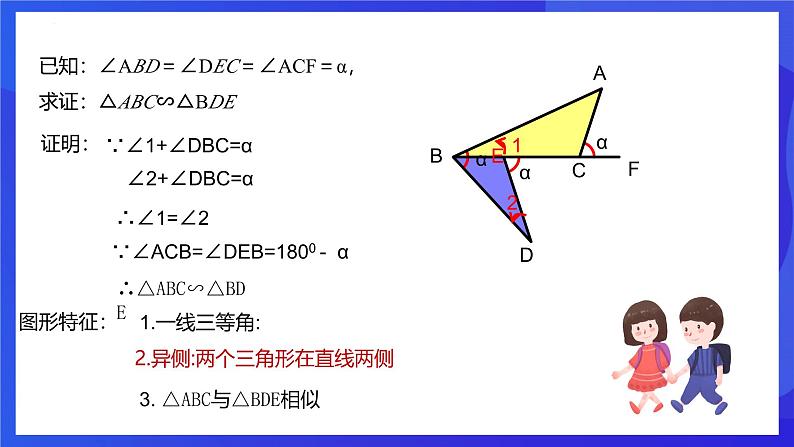
第四章 相似三角形章末复习 开心图形 相似三角形的判定：1、三边成比例的两个三角形相似2、两边成比例且夹角相等的两个三角形相似3、两角分别相等的两个三角形相似相似三角形的性质：1、对应角相等、对应边成比例；2、对应角平分线的比、对应中线的比、对应高线的比、周长的比等于相似比、3、面积的比等于相似比的平方 齐声朗读已知：∠B＝∠ACE＝∠D＝90°，求证：△ABC∽△CDE证明：∵∠ACD=∠1+900∠ACD=∠2+900∴∠1=∠2∴△ABC∽△CDA∵∠B=∠D=900图形特征：1.三等角，三等角的顶点在同一条直线上2. △ABC与△CDA相似几何模型：一线三等角+ k型新知讲解已知：△ABC和△CDE是任意三角形，∠B=∠ACE=∠D=α，求证△ABC ∽△CDE证明：∵∠ACD=∠1+α∠ACD=∠2+α∴∠1=∠2∵∠B=∠D=α∴△ABC∽△CDA几何模型：一线三等角+ k型+开心图形已知：△ABC和△CDE是任意三角形，∠B=∠ACE=∠D=β，求证△ABC ∽△CDE证明：∵∠1+β+∠ACB=1800∠2+β+∠ACB=1800∴∠1=∠2∵∠B=∠D=β∴△ABC∽△CDA已知：∠ABD＝∠DEC＝∠ACF＝90°，求证：△ABC∽△BDE证明：∵∠1+∠DBC=900∠2+∠DBC=900∴∠1=∠2∵∠ACB=∠DEB=900∴△ABC∽△BDE2.异侧:两个三角形在直线两侧1.一线三等角:图形特征：3. △ABC与△BDE相似已知：∠ABD＝∠DEC＝∠ACF＝α，求证：△ABC∽△BDE证明：∵∠1+∠DBC=α∠2+∠DBC=α∴∠1=∠2∵∠ACB=∠DEB=1800 - α∴△ABC∽△BDE图形特征：1.一线三等角:2.异侧:两个三角形在直线两侧3. △ABC与△BDE相似一线三等角 1. 如图，在△ABC中，AB＝AC，∠BAC＝108°，点D，E分别在边BC，AB上，且∠ADE＝36°. 求证：△ADC∽△DEB. 证明：∵在△ABC中， AB＝AC，∠BAC＝108°， ∴∠B＝∠C＝36°. ∵∠ADE＝36°，∴∠ADE＝∠B. ∵∠EDC＝∠ADE＋∠ADC＝∠B＋∠DEB， ∴∠ADC＝∠DEB. ∴△ADC∽△DEB. 当堂检测2.如图,在正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°,若AB=12,AE=3,CF=4,求CG的长3．如图，在等边△ABC中，AB＝12，P，Q分别是边BC，AC上的点，且∠APQ＝60°，PC＝8，则QC的长是___________． △ABP∽△PCQ图中找k型相似得比例比例来计算计算求线段4．如图，在矩形ABCD中，AB＝6，AD＝12，点E在AD边上，且AE＝8，EF⊥BE 交CD于点F.(1)求证：△ABE∽△DEF；(2)求CF的长．5 . 如图,在△ABO中, ∠AOB=90 º,点A在 上，点 在 上,且AO:BO=1： ，则 k值为 .-2 6.如图，已知：AB⊥DB于点B ，CD⊥DB于点D，AB=6，CD=4，BD=14.问：在DB上是否存在P点，使以C、D、P为顶点的三角形与以P、B、A为顶点的三角形相似？如果存在，计算出点P的位置；如果不存在，请说明理由。△ABP∽△CDP 6：4=（14―x）:xx=5.6△ABP∽△PDC6： x =（14―x）: 4∴x=2或x=12（2）若E为BC的中点，连结AF,图中有哪些相似三角形？△ABE∽ △ECF 9、如图,在等腰△ABC中, ∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B、C重合），在AC上取一点E，使∠ADE=45°（1）求证：△ABD∽△DCE证明：∵AB=AC，∠BAC=90°∴∠B=∠C=45°又∵∠ADE=45°∴∠ADE=∠B∵∠ADC是△ABD的外角∴∠ADC=∠ADE+∠2=∠B+∠1∴∠1=∠2∴ △ABD∽△DCE（2）设BD=x，AE=y，求y关于x的函数关系式及自变量x的取值范围，并求出当BD为何值时AE取得最小值解：∵△ABD∽△DCE分析：∠ADE=45°△ABD∽△DFEDF=4求证∠CEF=∠CDE△CEF∽△CDECD=5课程结束