




所属成套资源:2024-2025学年九年级数学下册同步教学课件(湘教版2024)
湘教版(2024)九年级下册2.5 直线与圆的位置关系课堂教学ppt课件
展开
这是一份湘教版(2024)九年级下册2.5 直线与圆的位置关系课堂教学ppt课件,共24页。PPT课件主要包含了☉O就是所求的圆,课堂小结等内容,欢迎下载使用。
1. 理解三角形的内切圆、三角形的内心等概念;2. 理解画三角形的内切圆的步骤,会画三角形的内切圆;3. 能能根据三角形的内切圆求角、边和内切圆半径(重难点)
阅读教材P72-74。用6分钟的时间看谁又快又好地解决以下问题:1、阅读教材P72-73的“议一议”“动脑筋”掌握三角形内切圆的定义及作法,理解内心和圆的外切三角形的概念;2、阅读P74的例题6,学会三角形内切圆的知识解决相关问题,并掌握做题的格式与步骤。
想在一块三角形硬纸板上剪下一个面积最大的圆形纸板,应当怎样剪?
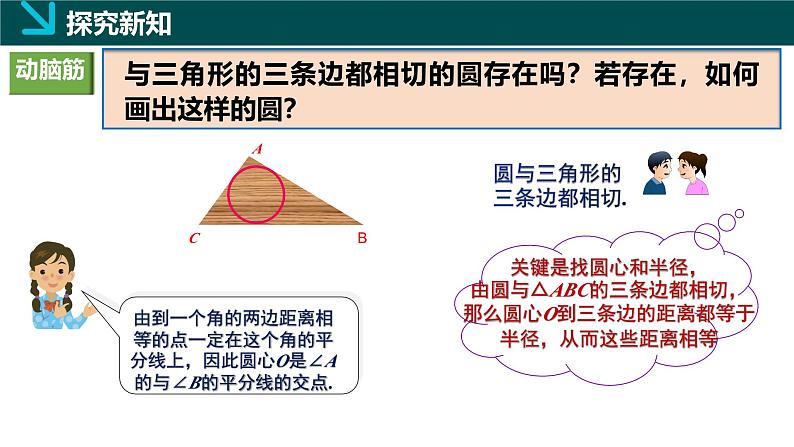
与三角形的三条边都相切的圆存在吗?若存在,如何画出这样的圆?
圆与三角形的三条边都相切.
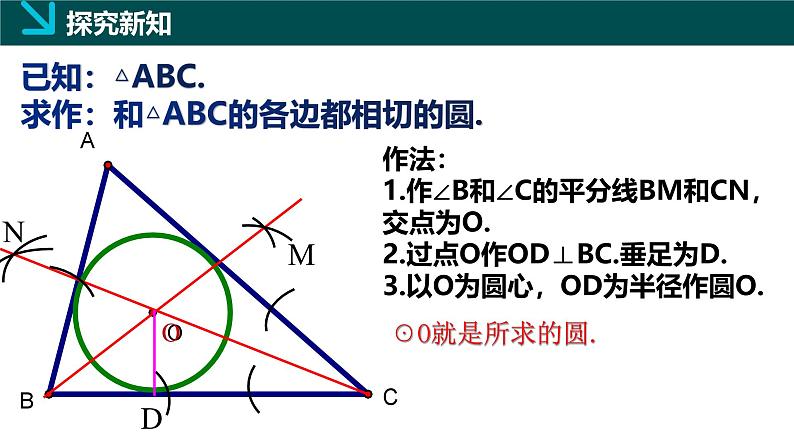
已知:△ABC.求作:和△ABC的各边都相切的圆.
作法:1.作∠B和∠C的平分线BM和CN,交点为O.2.过点O作OD⊥BC.垂足为D.3.以O为圆心,OD为半径作圆O.
1. 与三角形三边都相切的圆叫做三角形的内切圆.
2. 三角形内切圆的圆心叫做这个三角形的内心.
3. 这个三角形叫做这个圆的外切三角形.
内心三个内角的平分线的交点圆心到三边距离相等
三角形三边中垂线的交点
1.外心到三顶点的距离相等;2.外心不一定在三角形的内部
三角形三条角平分线的交点
1.内心到三边的距离相等;2.内心在三角形内部.
三角形内心与外心区别与联系
如图,⊙O是△ABC的内切圆,∠A=70°,求∠BOC的度数.
∴∠ABC+∠ACB=180°-∠ A=110°
∵⊙O是△ABC的内切圆
∴BO,CO分别是∠ABC和∠ACB的平分线
∴∠ BOC=180°-(∠ OBC+∠OCB) =180°- (∠ABC +∠ACB) =180° - ×110° = 125°.
有下列说法: ①内心一定在三角形内部; ②内心到各顶点的距离相等; ③内心是三角形三个内角平分线的交点; ④内心与外心重合的三角形是等边三角形.其中正确的有( ) A. 1 个 B. 2 个 C. 3 个 D. 4个
2. 如图为4×4的正方形网格,△ABC的顶点均在格点上,则下列各点中是△ABC的内心的是( )A. 点DB. 点EC. 点FD. 点G
3.如图,△ABC 的内切圆☉O 与 BC,CA,AB 分别相切于点 D,E,F,且 AB = 5,BC = 13,CA = 12,则阴影部分(即四边形 AEOF )的面积是( )A.4 B.6.25 C.7.5 D.9
5. 如图, 点 O 是△ABC 的内心,过点 O 作EF∥AB, 与 AC, BC 分别交于点 E, F,则( ) A.EF > AE + BF B.EF < AE + BF C.EF = AE + BF D.EF ≤ AE + BF
任画一个三角形,求作它的内切圆.
2. 如图,△ABC 的内切圆的三个切点分别为D,E,F, ∠A= 74°,∠B = 47°,求圆心角∠EOF 的度数.
解:∵△ABC的内切圆的三个切点分别为D,E,F,∴ OF⊥AC,OE⊥BC,OD⊥AB,∴∠OEC=∠OFC=90°.∵∠A= 74°,∠B= 47°,∴∠C=59°,∴∠EOF = 121°.
3. 已知等边三角形 ABC 的边长为 a, 求它的内切圆的半径.
解:如图,⊙O 是等边三角形ABC 的内切圆,连接OB, OC,则∠OBC= ∠B=30°,∠OCB= ∠C=30°.设BC 边与⊙O 的切点为D,连接OD,则OD⊥BC,且OD 为内切圆的半径.在Rt△OBD 与Rt△OCD 中,∴ BD=DC, 即 DC=即内切圆的半径长为
(3)若∠BIC=100 °,则∠A = 度.
(2)若∠A=80 °,则∠BIC = 度.
4、如图,在△ABC中,点I是内心, (1)若∠ABC=50°, ∠ACB=70°,∠BIC=_____.
(4)试探索: ∠A与∠BIC之间存在怎样的数量关系?
5、如图,△ABC中,I是内心,∠A的平分线和△ABC的外接圆相交于点D.求证:DI=DB.
证明:连接BI.∵I是△ABC的内心,∴∠BAD=∠CAD,∠ABI=∠CBI,∵∠CBD=∠CAD,∴∠BAD=∠CBD,∵∠BID=∠BAD+∠ABI,∠IBD=∠CBI+∠CBD,∴∠BID=∠IBD,∴BD=ID.
1、 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:由△ABC的内切圆⊙O切点为D、E、F
∴AE=AF=x,BD=BF=y,CD=CE=z
∴AC=AE+CE=x+z=9
AB=AF+BF=x+y=13
BC=BD+CD=y+z=14
∴x=4,y=9,z=5
∴AF=4,BD=9,CE=5
方法小结:关键是熟练运用切线长定理,将相等线段设为相同的未知数,从而建立方程求解.
2.如图,Rt△ABC 中,∠C = 90°,BC = a,AC = b,AB = c,☉O 为 Rt△ABC 的内切圆. 求 Rt△ABC 的内切圆的半径 r.
∵ ☉O 与 Rt△ABC 的三边都相切,
∴ AD = AF,BE = BF,CE = CD,
解:设 Rt△ABC 的内切圆与三边相切于 D、E、F,连接 OD、OE、OF,则 OD⊥AC,OE⊥BC,OF⊥AB.
设 AD = x , BE = y ,CE = r .
运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
内心(三角形三条角平分线的交点)
相关课件
这是一份湘教版(2024)九年级下册3.1 投影教课内容ppt课件,共26页。PPT课件主要包含了平行投影,中心投影,动脑筋,做一做,例题讲解,S1S<S2,课堂小结等内容,欢迎下载使用。
这是一份初中数学湘教版(2024)九年级下册2.6 弧长与扇形面积教课课件ppt,共1页。
这是一份初中数学湘教版(2024)九年级下册第2章 圆2.6 弧长与扇形面积教课课件ppt,共1页。









