北京市通州区2024-2025学年七年级上学期期末考试 数学试题（含解析）

这是一份北京市通州区2024-2025学年七年级上学期期末考试 数学试题（含解析），共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．一个有理数的绝对值是2，则这个数是（ ）
A．2B．C．D．
2．2024年国庆节期间，某著名景点在国庆七天共接待游客251700人，将251700用科学记数法表示为（ ）
A．B．C．D．
3．下列计算正确的是（ ）
A．B．
C．D．
4．下图是某几何体的展开图，该几何体是（ ）
A．三棱锥B．三棱柱C．四棱锥D．四棱柱
5．下列说法正确的是（ ）
A．是有理数，则B．是有理数，则
C．是有理数，则D．是有理数，则
6．下列运算正确的是（ ）
A．B．C．D．
7．关于单项式和多项式有下列说法：①单项式的系数是2；②单项式的次数是3；③多项式是三次三项式．其中正确的有（ ）
A．①②B．②③C．①③D．①②③
8．下列解方程中变形正确的有（ ）
①变形为；②变形为；③变形为；④变形为；⑤变形为．
A．①②④B．②③④C．①③⑤D．②④⑤
9．下列描述正确的是（ ）
A．如果，且，那么
B．如果，且，那么
C．如果，且，那么
D．如果，且，那么
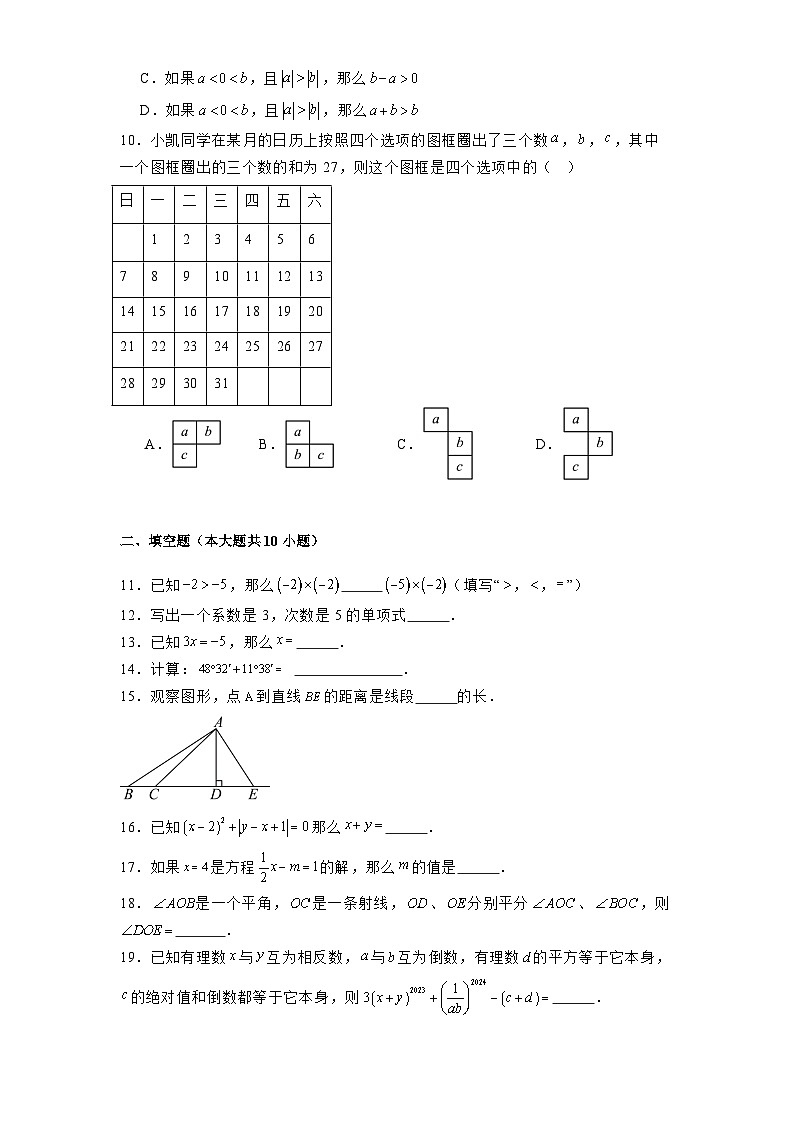
10．小凯同学在某月的日历上按照四个选项的图框圈出了三个数，，，其中一个图框圈出的三个数的和为27，则这个图框是四个选项中的（ ）
A．B．C．D．
二、填空题（本大题共10小题）
11．已知，那么 （填写“，，”）
12．写出一个系数是3，次数是5的单项式 ．
13．已知，那么 ．
14．计算： ．
15．观察图形，点到直线的距离是线段 的长．
16．已知那么 ．
17．如果是方程的解，那么的值是 ．
18．是一个平角，是一条射线，、分别平分、，则 ．
19．已知有理数与互为相反数，与互为倒数，有理数的平方等于它本身，的绝对值和倒数都等于它本身，则 ．
20．一副直角三角板如图1放置：直角三角板的边与直角三角板的边重合，点在线段的延长线上．如图2，将图1的直角三角板绕点以每秒的速度顺时针旋转（当射线与射线重合时停止），在旋转过程中始终平分，当满足时，三角板的运动时间为 ．
三、解答题（本大题共8小题）
21．计算：
(1)；
(2)．
22．解方程：
(1)；
(2)．
23．求代数式的值．
(1)，其中；
(2)，其中，．
24．已知，平面内三个点，，不在同一条直线上．
(1)按要求画图，保留画图痕迹；
①画线段，画射线，画直线；
②延长线段到点，使得；
③过点画直线，垂足为；④连接．
(2)观察你画出的图形，写出一个图形中正确的结论．
25．如图，，点是线段的中点，点是线段上一点，且，求线段的长．
26．七年级一班和二班两个班的同学到某公园开展社会大课堂活动，公园门票每人40元，超过40人可以购买团体票．每班的学生人数都超过40人．公园购票处张贴着团体优惠购票的方案表格如下．
团体票购票价格一览表
(1)一班有55名学生，他该选择哪个方案更省钱，说明理由；
(2)二班无论选择哪种方案付的钱是一样多，求二班有多少人．
27．如图，，是内部的两条射线，，，，求的度数．
28．对于数轴上，，三点，给出如下定义：若其中一个点与其他两个点的距离恰好满足2倍的数量关系，则称该点是其他两个点的“倍长点”．例如，数轴上点A，B，C所表示的有理数分别为0，2，3，此时点是点，的“倍长点”．
(1)数轴上点表示的有理数为，点表示的有理数为3，下列各数，0，，4，7所对应的点分别为，，，，，其中是点，的“倍长点”的是_____；
(2)数轴上点表示的有理数为，点表示的有理数为，点是数轴上的一个动点，对应的有理数用表示．若，且点，，中有一个点恰好是其他两个点的“倍长点”，则满足条件的的值有_____个；
(3)在（2）中，若为整数，则满足条件的整数的值是_____（用含有的代数式表示）．
参考答案
1．【答案】C
【分析】数轴上一个数到原点的距离叫做这个数的绝对值，据此进行解答即可．
【详解】解：一个有理数的绝对值是2，则这个数是．
故此题答案为C
2．【答案】A
【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值时，n是正数；当原数的绝对值时，n是负数．据此解答即可．
【详解】解：．
故此题答案为A．
3．【答案】D
【详解】A. ，故选项错误，不符合题意；
B. ，故选项错误，不符合题意；
C. ，故选项错误，不符合题意；
D. ，故选项正确，符合题意．
故此题答案为D
4．【答案】B
【分析】由展开图可得，该几何体三个面为正方形，两个面是三角形，据此可得该几何体是三棱柱．
【详解】解：由由展开图可得，该几何体三个面为正方形，两个面是三角形，
所以该几何体是三棱柱
故此题答案为B．
5．【答案】C
【分析】根据有理数的概念、倒数及有理数的乘方运算，根据题意逐项分析判断即可求解．
【详解】解：A. 是有理数，当或时，则，故该选项不正确，不符合题意；
B. 是有理数，当时，则，故该选项不正确，不符合题意；
C. 是有理数，则，故该选项正确，符合题意；
D. 是有理数，当时，则，故该选项不正确，不符合题意；
故此题答案为C．
6．【答案】D
【分析】利用合并同类项法则分析得出答案．
【详解】A选项错误，不是同类项无法合并；
B选项错误，正确应为；
C选项错误，不是同类项无法合并；
D选项正确．
故此题答案为D．
7．【答案】B
【分析】数字与字母的乘积是单项式，其中数字因数是单项式的系数，所有字母指数和是单项式的次数；多项式是几个单项式的和，单项式的个数是多项式的项数，最高次项的次数是多项式的次数判断即可．再逐一分析即可．
【详解】解：①单项式的系数是23，故①错误；
②单项式的次数是3，故②正确；
③多项式是三次三项式，故③正确．
故此题答案为B．
8．【答案】D
【分析】利用一元一次方程的求解方法：去分母，移项，合并同类项，系数化1，进行逐项分析，即可作答．
【详解】解：通过方程两边同时除以4，即系数化1，得，故①是不符合题意；
通过方程两边同时除以2，得，故②是符合题意；
通过方程两边同时减去，得，故③是不符合题意；
通过方程两边同时乘上，得，故④是符合题意；
通过方程两边同时乘上，即去分母，得，故⑤是符合题意；
故此题答案为D．
9．【答案】C
【分析】根据绝对值越大的数离数轴原点的距离越远，据此进行逐项分析，即可作答．
【详解】解：A、如果，且，那么，故该选项不符合题意；
B、如果，且，那么，故该选项不符合题意；
C、如果，且，那么，故该选项符合题意；
D、如果，且，那么，故该选项不符合题意；
故此题答案为C
10．【答案】B
【分析】先观察这个日历的情况，且结合各个选项的三个数，，的位置关系进行列式计算，注意，，都是正整数，即可作答．
【详解】解：A、设，则，
故，
解得，不是正整数，
故该选项不符合题意；
B、设，则，
故，
解得，
即，
故该选项符合题意；
C、设，则，
故，
解得，不是正整数，
故该选项不符合题意；
D、设，则，
故，
解得，不是正整数，
故该选项不符合题意；
故此题答案为B．
11．【答案】
【分析】先分别计算出式子的结果，再进行比较即可．
【详解】解：依题意，，，
，
，
12．【答案】（答案不唯一）
【分析】根据单项式的定义，再结合系数是3，次数是5，即可直接得出答案．
【详解】解：∵系数是3，次数是5，
∴该单项式可以是
13．【答案】
【分析】结合，再系数化1，即可作答．
【详解】解：∵，
∴系数化1，得
14．【答案】
【详解】解：
15．【答案】AD/
【分析】结合图形，得出线段是垂线段，即可作答．
【详解】解：依题意，结合图形，得出线段是垂线段，
∴点到直线的距离是线段的长
16．【答案】3
【分析】已知字母的值求代数式的值，因为，则，得，即可作答．
【详解】解：∵，
∴，
∴，
∴x=2，，
∴．
17．【答案】1
【分析】根据题意，把代入方程中，进而求出m的值．
【详解】解：把代入方程得，，
解得
18．【答案】90°/90度
【分析】根据、分别平分、，可得，，从而得到，即可求解．
【详解】解：∵、分别平分、，
∴，，
∴，
∵是一个平角，
∴，
∴．
19．【答案】或
【分析】根据相反数的应用、倒数、有理数的乘方运算、绝对值的意义可得，，或，，然后代入代数式求值即可．
【详解】解：∵有理数与互为相反数，与互为倒数，有理数的平方等于它本身，的绝对值和倒数都等于它本身，
∴，，或，，
∴或
20．【答案】32.5秒
【详解】解：由题意可得：，
∵，，
∴．
∵平分，
∴．
∵，
∴，
解得：．
21．【答案】(1)
(2)
【分析】（1）先算乘法，再算加法即可；
（2）先算乘方和括号内的式子，再算加减法即可．
【详解】（1）解：
（2）解：
22．【答案】(1)
(2)
【分析】（1）按照去括号、移项、合并同类项、系数化为1的步骤解方程即可得；
（2）按照去分母、去括号、移项、合并同类项、系数化为1的步骤解方程即可得．
【详解】（1）解：，
去括号，得，
移项，得，
合并同类项，得，
系数化为1，得．
（2）解：，
方程两边同乘以6去分母，得，
去括号，得，
移项，得，
合并同类项，得，
系数化为1，得．
23．【答案】(1)3
(2)5
【分析】（1）直接把代入进行计算，即可作答．
（2）先去括号再合并同类项，得，然后把，代入进行计算，即可作答．
【详解】（1）解：依题意，
当时，
，
（2）解：
，
当，时，
．
24．【答案】(1)见解析
(2)见解析（答案不唯一）
【分析】（1）根据射线、直线、线段的画法，垂线的画法，画出图形即可求解；
（2）根据两点之间线段最短即可得出
【详解】（1）解：如图所示，线段，射线，直线，线段、，，即为所求
（2）解：观察图形发现：．
25．【答案】的长为3或7
【分析】先用线段中点公式求出的长，再分点在点的左侧和右侧两种情况讨论：即可获得答案．
【详解】解：点是中点，
，，
，
（1）当点在线段上时，
，
，
，
（2）当点在线段上时，
，
，
的长为3或7．
26．【答案】(1)选择方案一，理由见解析
(2)二班有45人
【分析】（1）分别算出方案一和方案二的费用，再进行比较，即可作答．
（2）先设二班有人，再列出方程，然后解方程，即可作答．
【详解】（1）解：依题意，方案一：（元），
方案二：（元），
∵，
选择方案一；
（2）解：设二班有人，
根据题意得，
解得：，
答：二班有45人．
27．【答案】
【分析】设的度数为．结合，，，列式进行计算，即可作答．
【详解】解：设的度数为．
∵，，，
∴，
解得：，
28．【答案】(1)F，N
(2)6
(3)或
【分析】（1）根据数轴上两点距离计算公式分别求出点和点Q到，，，，5个点的距离，再根据“倍长点”的定义判断即可；
（2）先求出，，再分当A是B、T的“倍长点”时， 当B是A、T的“倍长点”时， 当T是A、B的“倍长点”时，三种情况根据 “倍长点”的定义建立方程求解即可；
（3）由（3）即可得到满足条件的整数的值．
【详解】（1）解：由题意得，，
，，
∴，
∴F，N是点P，Q的“倍长点”
（2）解：由题意得，，，
当A是B、T的“倍长点”时，则或，
∴或，
∴或；
当B是A、T的“倍长点”时，则或，
∴或，
∴或，
∴或或或（舍去）；
当T是A、B的“倍长点”时，则或，
∴或，
∴或，
∴或（舍去）或或，
综上所述，或或或或或，
∴t的值一共有6个；
（3）由（2）可知其中整数t的值为或日
一
二
三
四
五
六
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
人数优惠方案
40人以上
方案一
八折优惠（）
方案二
5人免票，其他人九折优惠