海南省海口市2024-2025学年七年级上学期1月期末考试 数学试题（含解析）

这是一份海南省海口市2024-2025学年七年级上学期1月期末考试 数学试题（含解析），共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
1．我国古代数学名著《九章算术》一书中明确提出“正负数”，这是世界上至今发现的最早的详细记载．如果水位上升7米记作+7米，那么水位下降3米记作（ ）
A．米B．3米C．4米D．米
2．南海之畔，共襄盛会．2024年11月22日，第十二届全国少数民族传统体育运动会在海南三亚开幕，56个民族欢聚一堂，5000多名演职人员向现场3.5万名观众呈现了一场海岛椰风中的沉浸式“大团圆”．将3.5万用科学记数法表示为（ ）
A．B．C．D．
3．下列计算正确的是（ ）
A．B．
C．D．
4．下列各式左右两边相等的是（ ）
A．B．
C．D．
5．若，，且，则的值为（ ）
A．B．C．或D．1或5
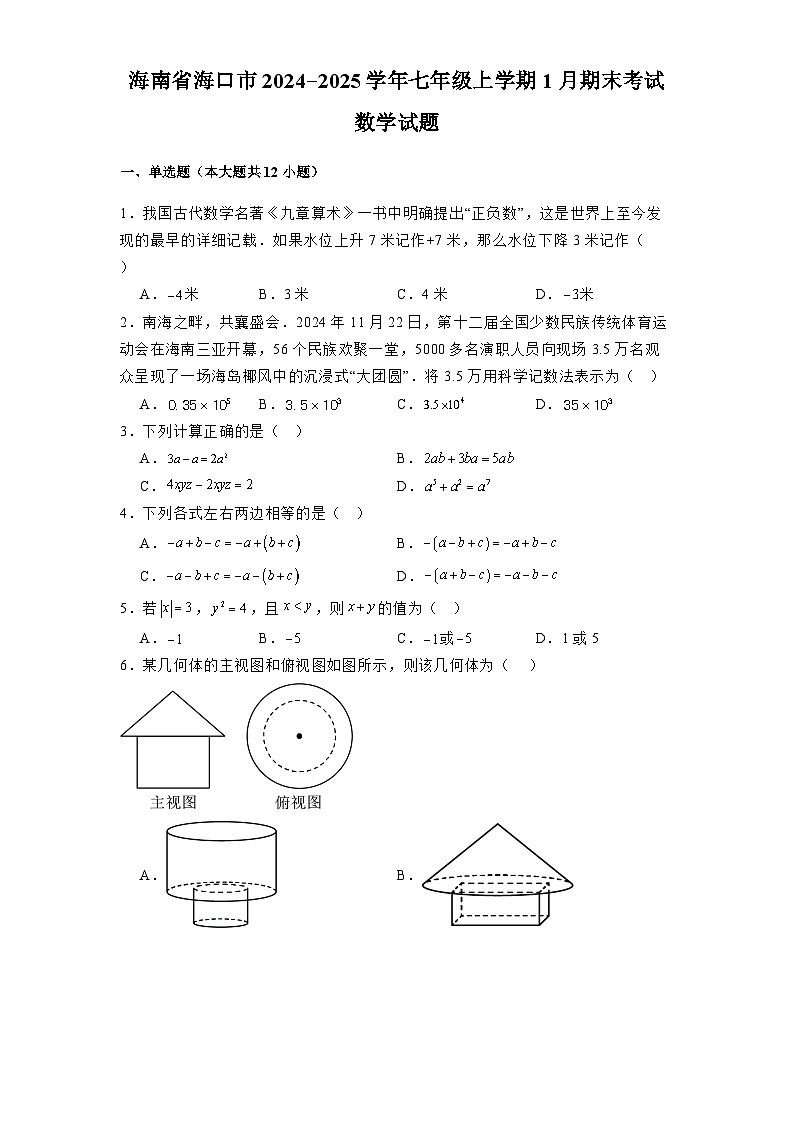
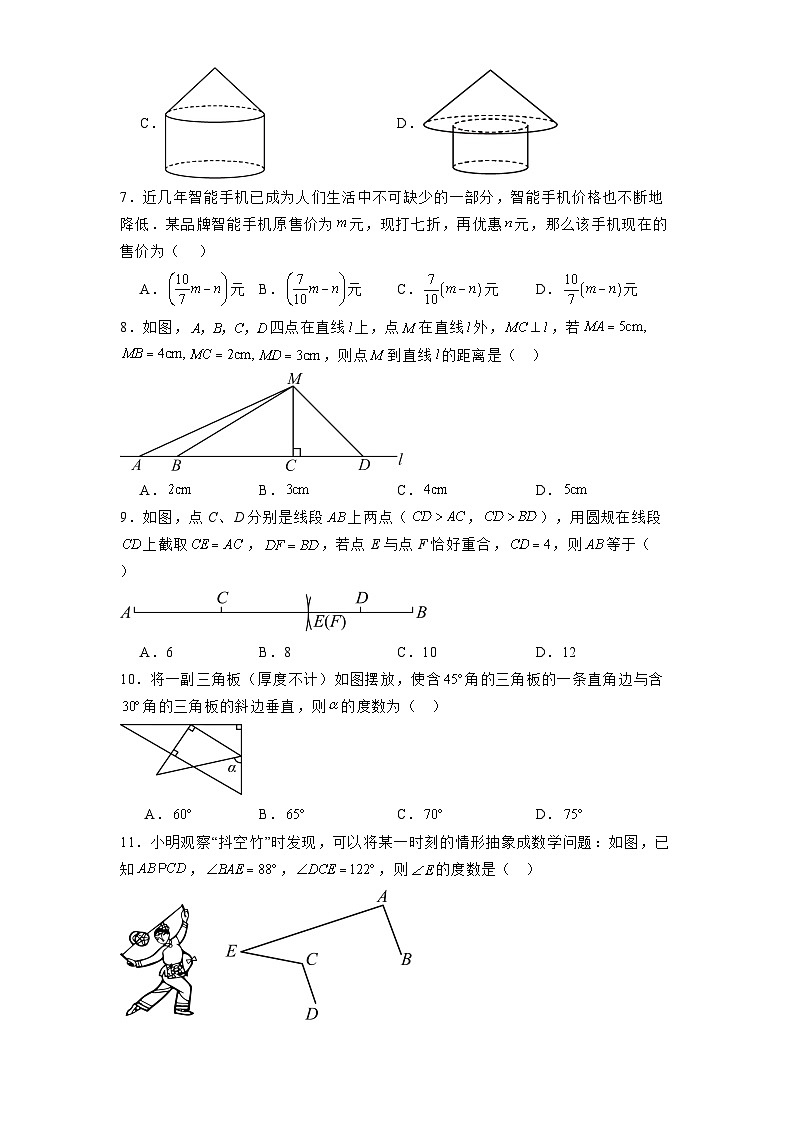
6．某几何体的主视图和俯视图如图所示，则该几何体为（ ）
A．B．
C．D．
7．近几年智能手机已成为人们生活中不可缺少的一部分，智能手机价格也不断地降低．某品牌智能手机原售价为元，现打七折，再优惠元，那么该手机现在的售价为（ ）
A．元B．元C．元D．元
8．如图，四点在直线上，点在直线外，，若，则点到直线的距离是（ ）
A．B．C．D．
9．如图，点C、D分别是线段上两点（，），用圆规在线段上截取，，若点E与点F恰好重合，，则等于（ ）
A．6B．8C．10D．12
10．将一副三角板（厚度不计）如图摆放，使含角的三角板的一条直角边与含角的三角板的斜边垂直，则的度数为（ ）
A．B．C．D．
11．小明观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知，，，则的度数是（ ）
A．B．30°C．D．
12．年月日，“雪龙”船返回上海国内基地码头，标志着中国第次南极考察圆满完成．如图，已知“雪龙”船上午时在市的北偏西方向上的点处，且在岛的西南方向上，则此时“雪龙”船与市和岛连线夹角的度数是（ ）
A．B．C．90°D．
二、填空题（本大题共4小题）
13．已知a，b互为相反数，则 ．
14．一个角的补角比它的余角的2倍还多20°,这个角的度数为 .
15．如图，要得到，则需要条件 （填一个你认为正确的条件即可），理由是 ．
16．如图，点O为直线上一点，过点O作射线，使．将直角三角板绕点O旋转一周，当直线与直线互相垂直时，的度数是 ．

三、解答题（本大题共6小题）
17．计算
(1)；
(2)；
(3)．
18．先化简，再求值：，其中，．
19．如图为海口市65路公交站牌的一部分．某天，小明参加志愿者服务活动，他从紫荆花园站出发，到从A站下车时，本次志愿者服务活动结束．如果规定向汇亚广场方向为正，向西秀海滩方向为负，当天的乘车站数按先后顺序依次记录如下（单位：站）：
+4，-3，+9，-8，+6，-2，-7，+3．
(1)请通过计算说明A站是哪一站?
(2)若相邻两站之间的平均距离为0.6千米，求这次小明志愿服务期间乘坐公交车行进的总路程约是多少千米?
20．如图，直线CD与直线AB相交于点．
(1)按要求完成画图．
过点画，交AB于点；
过点画，垂足为；
(2)在（）所画的图形中，按要求完成下列问题．
点到直线CD的距离是线段_________的长；
写出与的数量关系，并说明理由．
21．把四张形状大小完全相同的小长方形卡片（如图1），分两种不同形式不重叠的放在一个底面长为m，宽为n的长方形盒子底部（如图2，3），盒子底面未被卡片覆盖的部分用阴影表示．设图2中阴影部分图形的周长为，图3中两个阴影部分图形的周长的和为，
(1)用含m，n的式子表示图2阴影部分的周长
(2)若，求m，n满足的关系？
22．如图，四边形中，F为上一点，连接并延长，交的延长线于点E，连接．若，，．
(1)试说明；
解：（1）∵，（已知）
∴．（_______）
(2)与的位置关系如何？为什么？
解：与的位置关系是：，理由如下：
∵，（已知）
∴_______．（_______）
∵，（已知）
∴_______．（_______）
∵，（已知）
∴，
即______________，
∴_______．（等量代换）
∴．（_______）
(3)与相等吗？请说明理由．
参考答案
1．【答案】D
【分析】理解“正”和“负”的相对性，明确什么是一对具有相反意义的量．
【详解】解：如果水位上升7米记作+7米，那么水位下降3米记作米．
故此题答案为D
2．【答案】C
【分析】科学记数法的表示形式为的形式，其中，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．
【详解】解：3.5万即35000，
，
故此题答案为C．
3．【答案】B
【分析】根据合并合并同类项法则：把同类项的系数相加减，字母及字母的指数不变一一计算并判断即可．
【详解】解：．，原计算错误，故该选项不符合题意；
．，原计算正确，故该选项符合题意；
．，原计算错误，故该选项不符合题意；
．和不是同类项，不能合并，故该选项不符合题意；
故此题答案为B．
4．【答案】B
【详解】解：A、，选项错误，不符合题意；
B、，选项正确，不符合题意；
C、，选项错误，不符合题意；
D、，选项错误，不符合题意；
故此题答案为B．
5．【答案】C
【分析】根据绝对值的意义，乘方的意义，结合，确定x，y的值，计算即可．
【详解】解：∵，，
∴，，
∵，
∴，或，，
∴或，
∴的值为或，
故此题答案为C．
6．【答案】D
【分析】根据该几何体的主视图和俯视图，结合四个选项的几何体判断即可．
【详解】解：A．该几何体的主视图的上层是三角形，选项A的几何体的上层是矩形，故本选项不符合题意；
B．该几何体的俯视图是同心圆，选项B的俯视图不是同心圆，故本选项不符合题意；
C．该几何体的俯视图是一个圆（带圆心），故本选项不符合题意；
D．该几何体的主视图和俯视图符合题意，故本选项符合题意．
故此题答案为D
7．【答案】B
【分析】根据题意可得打九折后手机的价格为元，再优惠元后，手机的售价为元；
【详解】解：由题意得：打七折后手机的价格为元，
再优惠元后，手机的售价为元，
故此题答案为B
8．【答案】A
【详解】如图所示：
∵直线外一点到这条直线的垂线段最短，，
∴点M到直线l的距离是垂线段的长度，为，
故此题答案为A．
9．【答案】B
【分析】根据题意可得出．
【详解】解：∵，，点E与点F恰好重合，，
∴，
故此题答案为B
10．【答案】D
【分析】先证明，得到，进行求解即可．
【详解】解：如图，由题意，得：，
∴，
∴，
∴，
∴；
故此题答案为D．
11．【答案】D
【分析】首先过点作，根据两直线平行内错角相等可得：，根据两直线平行同位角相等可得：，，根据角之间的关系可得：，等量代换可得：．
【详解】解：如下图所示，过点作，
，，
，
，
又，
．
故此题答案为D．
12．【答案】A
【分析】首先根据两直线平行同位角相等可得：，再利用三角形内角和定理求出的度数．
【详解】解：如下图所示，
点在岛的西南方向上，
，
又，
，
点在市的北偏西方向上，
，
在中，．
故此题答案为A．
13．【答案】
【分析】利用整体思想求值即可．
【详解】解：∵a，b互为相反数，
∴
∴
14．【答案】20
【分析】设出所求的角为x，则它的补角为180°﹣x，余角为90°﹣x，根据题意列出方程，再解方程即可求解．
【详解】设这个角的度数是x，则它的补角为：180°﹣x，余角为90°﹣x；由题意得：
（180°﹣x）﹣2（90°﹣x）＝20°
解得：x＝20°．
15．【答案】 （答案不唯一） 同位角相等，两直线平行
【详解】解：要得到，利用平行线的判定：
①同位角相等两直线平行，可填；
②内错角相等两直线平行，可填；
③同旁内角互补两直线平行，可填；
16．【答案】或
【分析】分在直线的右侧和在直线的左侧两种情况求解即可．
【详解】解：∵，
∴．
当在直线的右侧时，如图，

∵，
∴，
∴．
当在直线的左侧时，如图，

∵，
∴，
∴．
17．【答案】(1)
(2)
(3)
【分析】（1）先算乘除法，最后再计算加减法．
（2）利用乘法运算律计算即可．
（3）先计算乘方，再计算括号里面的，最后再计算括号外面的．
【详解】（1）解：
（2）解：
（3）解：
18．【答案】，
【分析】先去括号，然后合并同类项，最后代入数值求解即可．
【详解】解：


当，时，
原式 ．
19．【答案】(1)A站是民声东路站
(2)总路程约是25.2千米
【分析】（1）求出这些数的和，根据和的符号和绝对值判断站的位置；（2）计算所有站数绝对值的和，再乘以即可．
【详解】（1）．
答：站是民声东路站．
（2）（千米）．
答：小明乘坐公交车行进的总路程约是千米．
20．【答案】(1)图见解析
图见解析
(2)
，理由见解析
【分析】（）按照作平行线的方法作图即可；
按照作垂线的方法作图即可；
（）由题意即可直接得出答案；
根据平行线的性质和平角的定义即可得出结论．
【详解】（1）解：如图所示：
即为所求作；
（2）解：由题意可知，点到直线CD的距离是线段的长
，理由如下：
∵，
∴，
∵，
∴．
21．【答案】(1)
(2)
【分析】（1）观察图形，可知，阴影部分的周长等于长方形的周长，计算即可；
（2）设小卡片的宽为x，长为y，则有，再将两阴影部分的周长相加，通过合并同类项即可求解，根据，即可求m、n的关系式．
【详解】（1）解：由图可知，阴影部分的周长等于长方形的周长，
故；
（2）设小长形卡片的宽为x，长为y，则，
∴，
所以两个阴影部分图形的周长的和为：
，
即为
∵，
∴
整理得：．
22．【答案】(1)同位角相等，两直线平行
(2)；两直线平行，同位角相等；；等量代换；；；；内错角相等，两直线平行
(3)相等，见解析
【分析】（1）根据同位角相等两直线平行即可判定．
（2）根据平行线的判定和性质求解即可．
（3）根据平行线的性质求解即可．
【详解】（1）解：∵，（已知）
∴．（同位角相等，两直线平行）
（2）解：与的位置关系是：，理由如下：
∵，（已知）
∴．（两直线平行，同位角相等）
∵，（已知）
∴．（等量代换）
∵，（已知）
∴．
即，
∴,（等量代换）
∴.（内错角相等，两直线平行）
（3）解：，理由如下：
∵，
∴．
∵，
∴．
∵，
∴．