人教A版 (2019)必修 第一册1.4.1 充分条件与必要条件教案

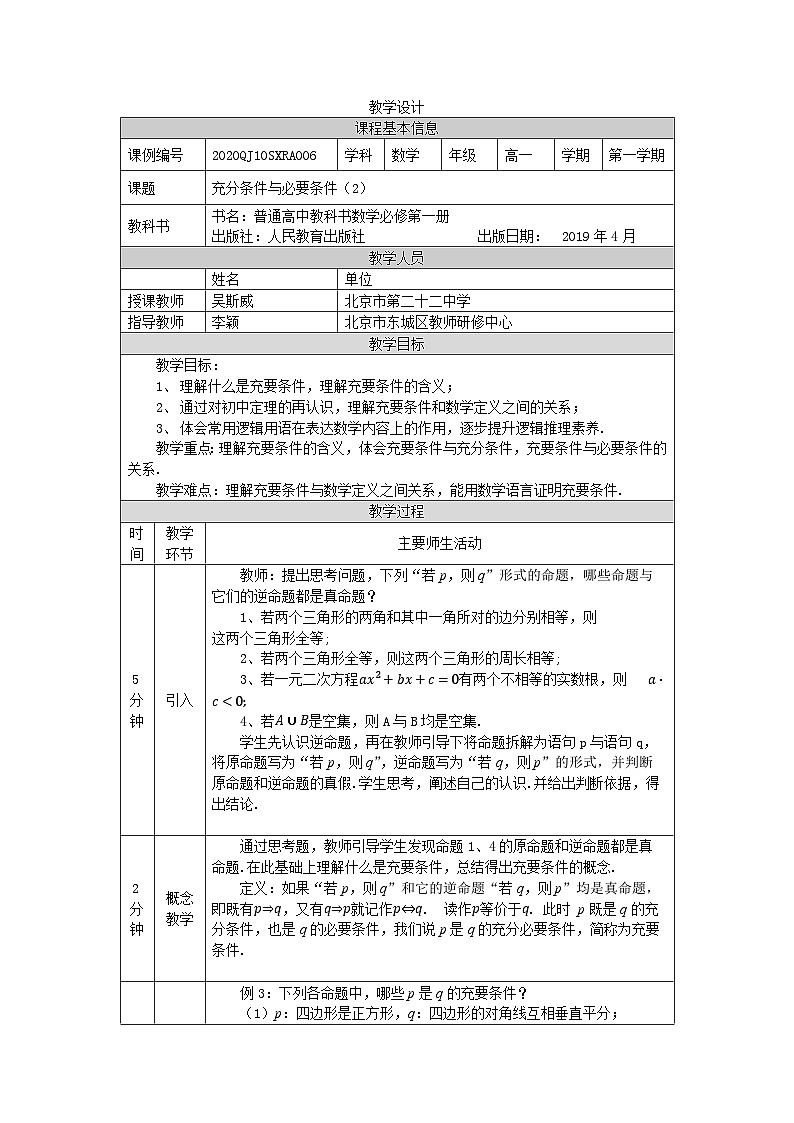
这是一份人教A版 (2019)必修 第一册1.4.1 充分条件与必要条件教案，共3页。

课程基本信息
课例编号
2020QJ10SXRA006
学科
数学
年级
高一
学期
第一学期
课题
充分条件与必要条件（2）
教科书
书名：普通高中教科书数学必修第一册
出版社：人民教育出版社 出版日期： 2019年4月
教学人员
姓名
单位
授课教师
吴斯威
北京市第二十二中学
指导教师
李颖
北京市东城区教师研修中心
教学目标
教学目标：
理解什么是充要条件，理解充要条件的含义；
通过对初中定理的再认识，理解充要条件和数学定义之间的关系；
体会常用逻辑用语在表达数学内容上的作用，逐步提升逻辑推理素养.
教学重点：理解充要条件的含义，体会充要条件与充分条件，充要条件与必要条件的关系.
教学难点：理解充要条件与数学定义之间关系，能用数学语言证明充要条件.
教学过程
时间
教学环节
主要师生活动
5分钟
引入
教师：提出思考问题，下列“若p，则q”形式的命题，哪些命题与它们的逆命题都是真命题？
1、若两个三角形的两角和其中一角所对的边分别相等，则
这两个三角形全等;
2、若两个三角形全等，则这两个三角形的周长相等;
3、若一元二次方程ax2+bx+c=0有两个不相等的实数根，则 a⋅c0，q:x>0，y>0；
（4）p:x=1是一元二次方程ax2+bx+c=0的一个根， q:a+b+c=0a≠0.
对于命题1，由于四边形的对角线互相垂直平分只能推出四边形是菱形，不能推出四边形是正方形，所以q⇏p，所以p不是q的充要条件；p是q的充分不必要条件.
对于命题2，两个三角形相似，可以由相似三角形性质定理推出两个三角形三边成比例.反之，由两个三角形三边成比例也可以推出两个三角形相似，这是相似三角形的判定定理，所以命题2中p是q的充要条件.
对于命题3 : 由xy>0，不仅能推出x>0时y>0，还可以推出x＜0时y＜0，所以p⇏q， p不是q的充要条件；p是q的必要不充分条件.
对于命题4，x=1是一元二次方程ax2+bx+c=0的一个根，将x=1 代入方程得到a+b+c=0a≠0；反之如果a+b+c=0a≠0那么当x=1时一定能够使一元二次方程ax2+bx+c=0成立.所以p是q的充要条件.
注意：通过例题，引导学生总结，判断p是q的充要条件，需要我们判断命题是否既有p⇒q，又有q⇒p.所以我们既要判断“若p，则q”是否为真，又要判断“若q，则p”是否为真.p⇒q，q⇒p，p是q的充要条件；p⇒q，q⇏p，p是q的充分不必要条件；p⇏q，q⇒p，p是q的必要不充分条件；p⇏q，q⇏p， p是q的既不充分也不必要条件.
3分钟
巩固练习
练习：下列各组命题中，p是q的什么条件？（请用“充分不必要条件”，“必要不充分条件”，“充要条件”，“既不充分也不必要条件”回答）
（1）p：三角形是等腰三角形，q：三角形是等边三角形；
（2）p：一元二次方程ax2+bx+c=0有实根，q:b2-4ac≥0;
（3）p:x>y，q:x2>y2;
（4）p:x>0，q：x＞-1.
问题1中由于语句p不能推出语句q，语句q可以推出语句p，所以p是q的必要不充分条件；
问题2中由于语句p能推出语句q，语句q也可以推出语句p，所以p是q的充要条件；
问题3由于语句p不能推出语句q，语句q不能推出语句p，所以p是q的既不充分也不必要条件；
问题4由于语句p能推出语句q，语句q不能推出语句p，所以p是q的充分不必要条件.
8分钟
探究思考
提问学生：你能给出“四边形是平行四边形”的充要条件吗？
学生思考并回答.
注意：
通过问题，结合以往的学习经验，发现“四边形的两组对边分别平行”，“四边形的一组对边平行且相等”，“四边形的两组对边分别相等”，“四边形的对角线互相平分”，均是“四边形是平行四边形”的充要条件.说明充要条件并不唯一. 上面四条都可以作为平行四边形的定义，而这些新的定义方式，分别从不同的侧面刻画了平行四边形.使学生进一步理解定义与充要条件之间的关系.
8分钟
能力提升
例4：已知圆O的半径为r，圆心O到直线l的距离为d.
求证：d=r是直线l与圆O相切的充要条件.
分析：证明分为两个部分，我们把充分性的证明和必要性的证明分开.这样便于理清证明思路.
设 p:d=r，q:直线l与圆O相切.
（1）先来证明充分性：如图，做OP⊥l于点P，则OP=d.若d=r，则点P在圆O上.在直线l上任取一点Q（异于点P），连接OQ.在直角三角形OPQ中，OQ＞OP=r.所以，除点P外直线l上的点都在圆O外部，即直线l与圆O仅有一个公共点P，所以直线l与圆O相切.
（2）再来证明必要性：若直线l与圆O相切，不妨设切点为P，则OP⊥l.因此d= OP =r.
综合（1）（2）可得，d=r是直线l与圆O相切的充要条件.
注意：
通过例题，学习充要条件的证明方法，要证明两个命题是否为充要条件关系，需要我们将问题分为充分性的证明和必要性的证明两个部分分别进行，这样既有利于思考清晰，又有利于书写清楚.结合实际问题进一步体会充要条件的含义.
在解决问题的过程中注意指导学生学习数学语言的表达方法，进一步强调将命题拆分为“若p，则q”和它的逆命题“若q，则p”的形式再判断真假.同时认识到充要条件是进行等价转化的机遇.
1分钟
总结新知
最后我们一起来总结一下本节课的学习内容：
1、对于语句p和语句q，如果p⇒q，q⇒p，那么p是q的充要条件；
2、判断充要条件的过程是将原命题改写成逆命题，再判断原命题和逆命题是否为真；
3、证明充要条件要关注两个方面，既要证明充分性，又要证明必要性；
4、体会充要条件和定义间的关系;
5、认识到在推理证明中充要条件是进行等价转化的重要机遇.