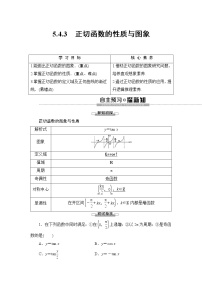
高中数学人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质5.4.3 正切函数的性质与图象教学设计

这是一份高中数学人教A版 (2019)必修 第一册第五章 三角函数5.4 三角函数的图象与性质5.4.3 正切函数的性质与图象教学设计，共7页。
课程基本信息
课例编号
2020QJ10SXRA052
学科
数学
年级
高一
学期
第一学期
课题
正切函数的性质和图象
教科书
书名：普通高中教科书数学必修第一册A版
出版社：人民教育出版社 出版日期： 2019年6月
教学人员
姓名
单位
授课教师
白芳
北京市第二十七中学
指导教师
李颖
北京市东城区教师研修中心
教学目标
教学目标：
1.初步理解正切函数的基本性质，并借助性质把握图象特征；
2.通过正切函数的图象和性质的研究，进一步体会函数研究的方法，体会数形结合和类比的思想方法的使用；
3.在正切函数的研究中，发展直观想象和数学抽象的素养.
教学重点：正切函数的周期性、定义域、值域、奇偶性和单调性，结合性质绘制图象.
教学难点：能够应用正切函数的图象和性质解决相关问题.
教学过程
时间
教学环节
主要师生活动
2分钟
复习引入
问题1：什么叫正切函数？
我们已经知道，对于任意一个角，，有唯一确定的正切值与之对应，因此是一个函数，称为正切函数.
设计意图：为研究正切函数的性质与图象作好准备.
问题2：如何研究正切函数的性质与图象？
前面我们研究正弦函数的方法是通过定义和单位圆绘制出正弦曲线，再通过图象直观地研究正弦函数的性质。研究余弦函数是利用正弦曲线平移得到余弦曲线，进而研究性质。正切函数的图像不能通过平移得到，但有了前面的知识准备，我们可以换个角度，即从正切函数的定义出发研究它的部分性质，再利用性质研究正切函数的图象，进而得到其他性质.
设计意图：在回顾研究正弦函数、余弦函数的方法的基础上引出研究正切函数的方法.
12分钟
新课讲解
正切函数的性质
1.定义域
由正切函数的定义，角的终边不能落在y轴上，因此我们得到正切函数的定义域： .
这种表示形式是在实数集中去掉了不能取到的点，还有没有其他的表达方法呢？我们也可以把能取到的所有值用区间形式表示出来，即.在这个形式中，每一个取定的k值就对应着一个具体的区间，比如当k=0时，对应的区间是，当 k=1时，对应的区间是，当 k=-1时，对应的区间是等，定义域应取这些区间的并集，用连接.
问题3：由此想象图象会具有什么特点？
图象被垂直于x轴的无穷多条直线隔开，两条直线之间的图象是连续的.
2.奇偶性
正切函数的定义域关于原点对称，由诱导公式且,可知，正切函数是奇函数.
问题4：由此想象图象会具有什么特点？
正切函数的图象关于原点对称.
3.周期性
由诱导公式，且,可知，正切函数是周期函数，周期是.
问题5：正切函数的周期性和奇偶性对研究它的图象会有什么帮助？
由于为正切函数的周期，所以我们只需要画出他在一个周期内的图象，然后通过平移就可以得到在整个定义域内的图象.选择哪一个长度为的区间呢？可以选择区间；而正切函数又是奇函数，所以只需画出在的图象.
下面我们研究怎样得到函数的图象.
正切函数的图象
我们可以利用描点法作出图象，为了更准确地得到点的坐标，我们可以利用单位圆找到正切值的几何意义.
如图5.4—9，设，在直角坐标系中画出角x的终边与单位圆的交点过点作轴的垂线，垂足为；过点作轴的垂线与角的终边交于点，则；由此可见，当时，线段的长度就是相应角的正切值．我们可以利用线段画出函数的图象，如图所示．
通过动画演示，将的角四等分，通过线段AT找到对应角的纵坐标，若希望更准确的绘图，可进一步取更多的点，用光滑曲线连结取到的点，得到的图象.
设计意图：通过正切函数定义及单位圆找到正切值得几何表示（即正切线），绘制正切函数的图象.
将函数的图象关于原点对称，就可得到函数 的图象；将函数的图象向左、右平移，每次平移个单位，就可得到正切函数，且的图象.
，且的图象，称为“正切曲线”.
从图可以看出，正切曲线是被与轴平行的一系列直线所隔开的无穷多支形状相同的曲线组成的.
问题6：由正切曲线，我们能够得到正切函数的哪些其他性质呢？
4.单调性
观察正切曲线可知，正切函数在区间上单调递增.由正切函数的周期性可得，正切函数在每一个区间,上都单调递增.
应注意：（1）区间端点不在定义域内，所以必须写成开区间；
（2）正切函数在每一个开区间,上都是单调递增的.k的每一个取定的值都对应着一个单调区间，而正切函数的定义域是这无穷多个区间的并，故正切函数在其整个定义域内不具有单调性.
5.值域
当时，在内可取到任意实数值，但没有最大值、最小值.因此，正切函数的值域是实数集.
6.渐近线
正切函数的图象是被相互平行的直线隔开的无穷多支形状完全相同的曲线组成的.当x趋近于时，函数值趋近于正无穷或负无穷，为其渐近线.
7.对称性
问题7：正切曲线有对称中心吗？
由于正切函数是奇函数，不难看出正切曲线是中心对称图形，原点就是它的一个对称中心，还有别的对称中心吗？正切曲线与x轴的每一个交点 都是其对称中心；另外，每条渐近线与x轴的交点也是其对称中心.
由此可知，正切曲线的对称中心为.
应注意，正切函数的对称中心除了函数图象与x轴的交点外，还有渐近线与轴的交点.对称中心不一定在图象上，比如我们熟悉的反比例函数，原点是其对称中心，但并不在函数图象上.
正切曲线无对称轴.
8.零点
观察正切曲线可以看出，正切函数的零点为.
以上我们研究正切函数的思路是：通过定义得到部分性质，在性质的辅助下得到正切函数图象，再由图象得到其他性质，将函数的性质与图象有机的结合起来，充分地体现了数形结合的思想.
设计意图：通过研究正切函数的性质画出正切函数图象，再通过图象发现更多性质.在解决问题的过程中由数想形，由形到数，反复进行数形转化.从定义、诱导公式、图象等多角度认识正切函数的性质与图象.
下面我们利用性质解决一些问题.
6分钟
例题解析
例1.不求值，分别比较下列各组正切值的大小.
（2）与的大小.
例2. 求函数的定义域、周期及单调区间.
分析：利用正切函数的性质，通过代数变形可以得出相应的结论.
解：自变量x的取值应满足：
即
所以，函数的定义域是.
设，又
所以
即
因为,
都有
所以，函数的周期为.
由
解得；
因此，函数在区间 , 上单调递增.
设计意图：应用正切函数的性质解决问题，加深对性质的理解，熟悉相关思想方法的应用.
1分
总结提升
这节课，我们通过正切函数的定义、结合诱导公式等得出了函数的一些性质，进而利用性质指导我们画出了正切函数的图象，再利用图象帮助我们发现了更多的性质，帮助我们理解性质，并利用性质与图象解决了有关问题。在解决问题的过程中运用了类比、整体代换、数形结合等思想方法．这样研究函数的方法值得同学们思考与借鉴.