人教A版（2019）高一数学必修第一册指数幂运算-教学设计

这是一份人教A版（2019）高一数学必修第一册指数幂运算-教学设计，共5页。
课程基本信息
课例编号
2020QJ10SXRA026
学科
数学
年级
高一
学期
第一学期
课题
指数幂运算
教科书
书名:普通高中教科书数学必修第一册A版
出版社：人民教育出版社 出版日期：2019 年 6 月
教学人员
姓名
单位
授课教师
刘鹏
北京市第一六六中学
指导教师
李颖
北京市东城区教师研修中心
教学目标
教学目标：
1. 熟练完成有理数指数幂的运算，了解指数幂的拓展过程与原理，掌握指数幂的运算性质；
2. 类比用有理数逼近无理数体会从“数”与“形”的两个角度，理解由有理数指数幂逼近无理数指数幂的原理，渗透逼近思想和极限思想；
3. 在信息技术的帮助下加深对无理数指数幂的理解，发展数学运算和数学抽象的素养。
教学重点：
实数指数幂的运算及其性质；
教学难点：
用有理数指数幂逼近无理数指数幂以及对无理数指数幂的理解.
教学过程
时间
教学环节
主要师生活动
2
5
15
2
引入
指数运算例题
无理数指数幂
总结
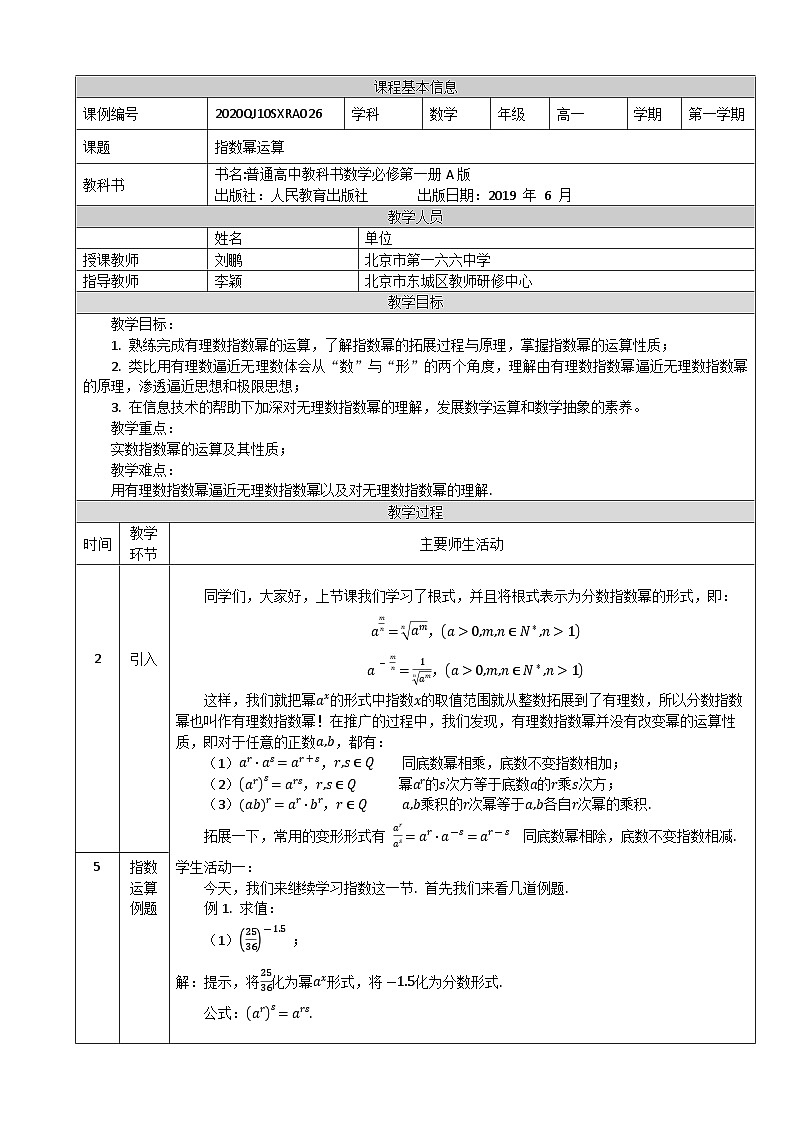
同学们，大家好，上节课我们学习了根式，并且将根式表示为分数指数幂的形式，即：
amn=nam，a>0,m,n∈N*,n>1
a-mn=1nam，a>0,m,n∈N*,n>1
这样，我们就把幂ax的形式中指数x的取值范围就从整数拓展到了有理数，所以分数指数幂也叫作有理数指数幂！在推广的过程中，我们发现，有理数指数幂并没有改变幂的运算性质，即对于任意的正数a,b，都有：
（1）ar∙as=ar+s，r,s∈Q 同底数幂相乘，底数不变指数相加；
（2）ars=ars，r,s∈Q 幂ar的s次方等于底数a的r乘s次方；
（3）abr=ar∙br，r∈Q a,b乘积的r次幂等于a,b各自r次幂的乘积.
拓展一下，常用的变形形式有 aras=ar∙a-s=ar-s 同底数幂相除，底数不变指数相减.
学生活动一：
今天，我们来继续学习指数这一节. 首先我们来看几道例题.
例1. 求值：
（1）2536-1.5 ；
解：提示，将2536化为幂ax形式，将-1.5化为分数形式.
公式：ars=ars.
2536-1.5=562-32=56-3=216125.
（2）23×331.5×612 .
解：提示，将各因子化为幂ax形式. 23×331.5×612=2×312×3×3213×1216.
回忆幂的运算性质，我们应该寻找相同的底数！
312，3213=313×2-13，1216=3×2216=316×213
公式：amn=nam，ar∙as=ar+s，aras=ar-s.
所以，23×331.5×612=2×312×3×3213×1216=2×312×3×313×2-13×316×213
=21-13+13×312+1+13+16=2×32=18.
总结：
尽量用指数幂的形式来表示根式，这样往往会简化根式运算.
指数幂的运算尽量化为同底数，即便不能化为同底，也要尽可能地减少不同底数的数量，同底才能运用运算性质.
例如：23×331.5×612=2×312×3×3213×1216
=2×312×3×313×2-13×316×213
学生活动二：
进一步引深，同学们有没有想过一个大胆的问题，指数有没有可能是无理数？也就是无理数指数幂！
首先我们复习一下无理数的知识. 整数和分数统称为有理数，分数又可写成有限小数和无限循环小数，而无理数又叫做无限不循环小数，例如2，3，π都是无理数，有理数和无理数统称实数.
通过初中的学习，我们已经知道，每一个无理数都是一个定值，能够用数轴上的一个点表示. 那么，如果不用计算器，我们如何来估算2的值呢？同学们可能会想到下面这种方式：
因为12=1