人教A版（2019）高一数学必修第二册--正弦定理、余弦定理的简单应用-1教案

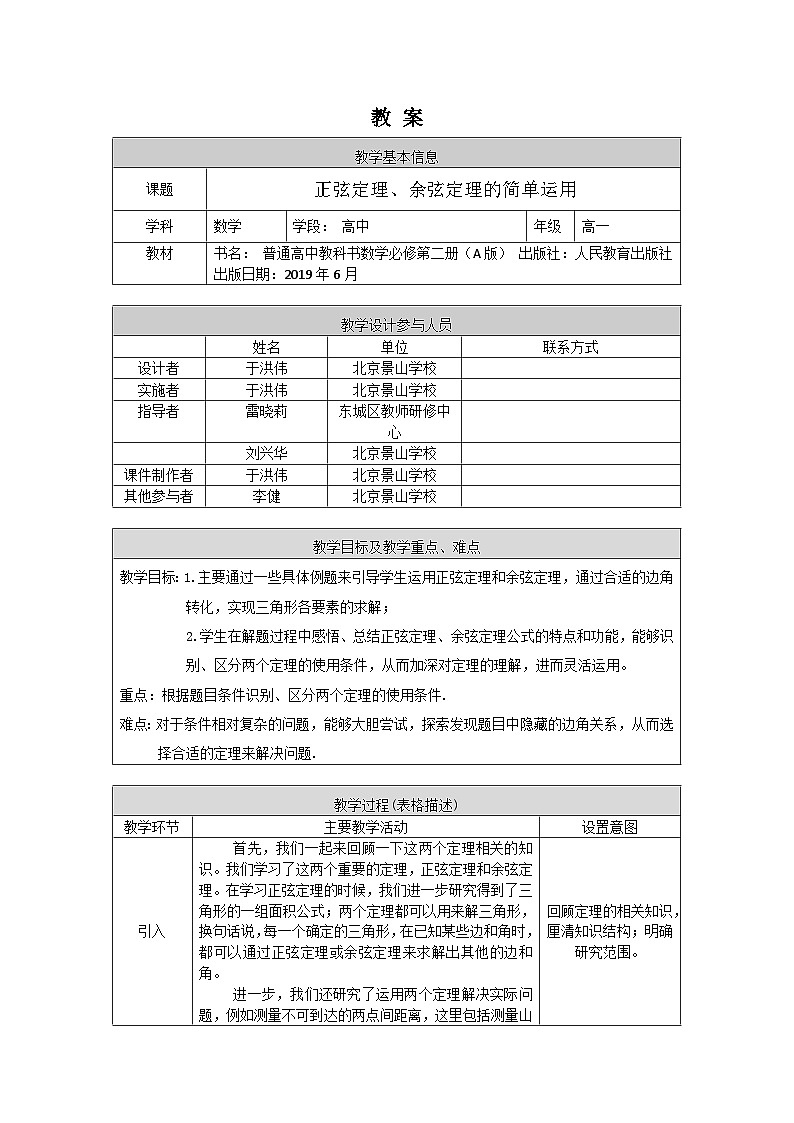
这是一份人教A版（2019）高一数学必修第二册--正弦定理、余弦定理的简单应用-1教案，共7页。

教学基本信息
课题
正弦定理、余弦定理的简单运用
学科
数学
学段： 高中
年级
高一
教材
书名： 普通高中教科书数学必修第二册（A版） 出版社：人民教育出版社
出版日期：2019年6月
教学设计参与人员
姓名
单位
联系方式
设计者
于洪伟
北京景山学校
实施者
于洪伟
北京景山学校
指导者
雷晓莉
东城区教师研修中心
刘兴华
北京景山学校
课件制作者
于洪伟
北京景山学校
其他参与者
李健
北京景山学校
教学目标及教学重点、难点
教学目标：1.主要通过一些具体例题来引导学生运用正弦定理和余弦定理，通过合适的边角转化，实现三角形各要素的求解；
2.学生在解题过程中感悟、总结正弦定理、余弦定理公式的特点和功能，能够识别、区分两个定理的使用条件，从而加深对定理的理解，进而灵活运用。
重点：根据题目条件识别、区分两个定理的使用条件.
难点：对于条件相对复杂的问题，能够大胆尝试，探索发现题目中隐藏的边角关系，从而选择合适的定理来解决问题.
教学过程(表格描述)
教学环节
主要教学活动
设置意图
引入
首先，我们一起来回顾一下这两个定理相关的知识。我们学习了这两个重要的定理，正弦定理和余弦定理。在学习正弦定理的时候，我们进一步研究得到了三角形的一组面积公式；两个定理都可以用来解三角形，换句话说，每一个确定的三角形，在已知某些边和角时，都可以通过正弦定理或余弦定理来求解出其他的边和角。
进一步，我们还研究了运用两个定理解决实际问题，例如测量不可到达的两点间距离，这里包括测量山高，测量河两岸的距离等等很多非常有价值的实际问题。在这里我们感受了数学的力量，以及其在实际生活中的价值。而研究三角形的性质，除了求解三角形的边角之外，还有很多的性质可以研究，比如：判断三角形的形状，求边角之外相关的几何量，包括周长、面积以及高线、中线、角分线等三角形的有关线段，还有求三角形相关的最值问题等等。
这节课，我们重点来研究两个定理的特点，识别定理的功能，探究在解三角形时如何区分、选用合适的定理来解决问题。
回顾定理的相关知识，厘清知识结构；明确研究范围。
新课
回顾定理内容：
分析正弦定理的功能
正弦定理适用情形：
已知两角及任一边；
已知两边及一边对角.(关注多解条件)
正弦定理可用但不方便的情形：
已知两边及夹角.
分析余弦定理的功能
余弦定理适用情形：
已知两边及夹角；
已知三边；
已知两边及一边对角.(对多解情况的判断更为方便和清晰)
总结两个定理的功能
总结定理的适用条件，为解决具体问题做准备。
回顾定理，对所学知进行梳理，提升认识，获得经验。
例题
例1：在中，已知，，，求边的值.
【分析】根据三角形内角和求出角，再根据正弦定理即可求出边．
【解答】因为，
所以根据正弦定理知，，即，
解得．
小结：已知两角及一角对边，求第三个角所对边，使用正弦定理并不能直接求解。我们联合使用了三角形内角和定理和正弦定理来解三角形，事实上，在解三角形时，内角和定理常常和正弦定理结合使用，两个公式各有自己的功能。我们可以注意到，在已知两角及一边解三角形时，会用到三角形内角和定理来求第三个角，然后在已知三个角的条件下，运用正弦定理求其它边。
例2：设a，b，c分别为△ABC内角A，B，C的对边，已知a=2，b＝1，c=5，求角C的值．
【分析】利用余弦定理即可求解．
【解答】解：∵a=2，b＝1，c=5，
∴由余弦定理得：csC=a2+b2-c22ab=-22，
又∵C∈（0，π），∴C=3π4，故答案为：3π4．
例3：在中，角、、的对边边长分别是、、，若，，，求的值．
【分析】直接利用正弦定理求出，求出，然后求解即可．
【解答】解：，，，
，所以．角、、是中的内角．
，，
．
故答案为：2．
也可运用余弦定理来求解。
小结：在已知两边及一边对角时，两个定理解题的差异及各自的优势.
例4：在△ABC中，内角A，B，C的对边分别为a，b，c，已知2bcsC＝2a+c．
求角B值．
【分析】直接由已知条件和正弦定理求出B的值．
【解答】解：（I）由已知以及正弦定理，
可得：2sinBcsC＝2sinA+sinC＝2sin（B+C）+sinC＝2sinBcC+2csBsinC+sinC，
所以：2csBsinC+sinC＝0，
由于：0＜C＜π，sinC≠0，所以csB=-12，
因为B∈（0，π），解得：B=2π3；
这道题目也可以用余弦定理来求解.
小结：在对边角关系进行转化时，两个定理的功能差异。
例5：在中，，求角的值.
【分析】由已知及正弦定理知，不妨设，则，，利用余弦定理即可解得的值，结合的范围即可得解的值．
【解答】解：因为，
所以由正弦定理知，
不妨设，则，，
则由余弦定理可得：，
因为，所以．
小结：正弦定理、余弦定理联合使用来解题，需要考虑什么条件下选择正弦定理，什么条件下选择余弦定理。一般来说，已知角的信息较多时，常常优先选择运用正弦定理，已知边的信息较多时，常常优先选择运用余弦定理，但事无绝对，在条件需要转化时，还需要具体问题具体分析。
例6：在中，若，，，求的值．
【分析】根据，，，利用余弦定理可得，即可求得的值．
【解答】解：由题意，，，，
故答案为：4
小结：合理转化边角关系，提高方程意识，重视方程思想。解题中，题目条件不一定刚刚好满足总结的定理结构需要我们适当转化，去匹配已有经验，适当调整，寻求解决办法。解题中的困难要灵活处理.
例7：锐角△ABC的内角A，B，C的对边分别是a，b，c，b＝1，ccsB=2sinA-csC，求B值．
【分析】由已知利用余弦定理可得a=2sinA，由正弦定理可得sinB的值，结合B为锐角可得B的值．
【解答】解：∵ccsB=2sinA-csC，
∴由余弦定理可得：
c•a2+c2-b22ac+a2+b2-c22ab=2sinA，
又∵b＝1，
∴a2+c2-12a+a2+1-c22a=2sinA，
可得a=2sinA，
∴由正弦定理可得bsinB=asinA=2，由b＝1，可得sinB=22．
∴由B为锐角可得B=π4．
故答案为：π4．
小结：当条件结构特征不明显时，需要适当转化，发现新的边角关系，得到结构明显的等价条件，在运用经验解题. 这其中，正弦定理和余弦定理联合使用，在完成边角关系转化中，要根据具体问题具体分析，敢于尝试，敢于探索.
运用总结的经验来解题，并在解题过程中不断丰富总结的经验，提升认识，提升数学素养.
总结
在面对具体问题时，我们首先分析条件.
如果条件结构较好，可以直接运用两个定理解三角形；如果条件结构不是特别明显，就先尝试运用定理来做边角转化，得到结构明显的等价条件，再根据结构来选择合适的定理解三角形.
回顾整节课不断在解题中积累经验的过程，提炼更高层次解题策略和指导思想，获得深层地的理解.
作业
1. 在△ABC中，，，，求角C的值.
2.已知△ABC的内角A、B、C所对的边分别为a、b、c，若a+b＝2c，3c＝5b，求A值．
巩固练习，检测本节课所获得的知识和经验的落实.