数学七年级下册（2024）第七章 相交线与平行线7.2 平行线7.2.2 平行线的判定示范课ppt课件

这是一份数学七年级下册（2024）第七章 相交线与平行线7.2 平行线7.2.2 平行线的判定示范课ppt课件，共38页。PPT课件主要包含了由此说明了什么，简单说成，判定方法1，同位角，应用新知，解这两条直线平行，平行线的判定方法2，还有其他解法吗，平行线的判定方法3，总结应用等内容，欢迎下载使用。
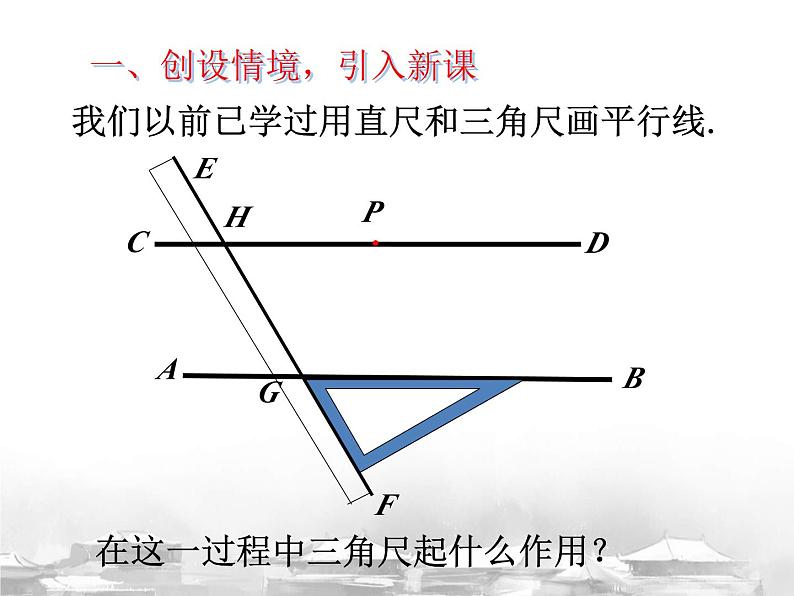
一、创设情境，引入新课
我们以前已学过用直尺和三角尺画平行线.
在这一过程中三角尺起什么作用？
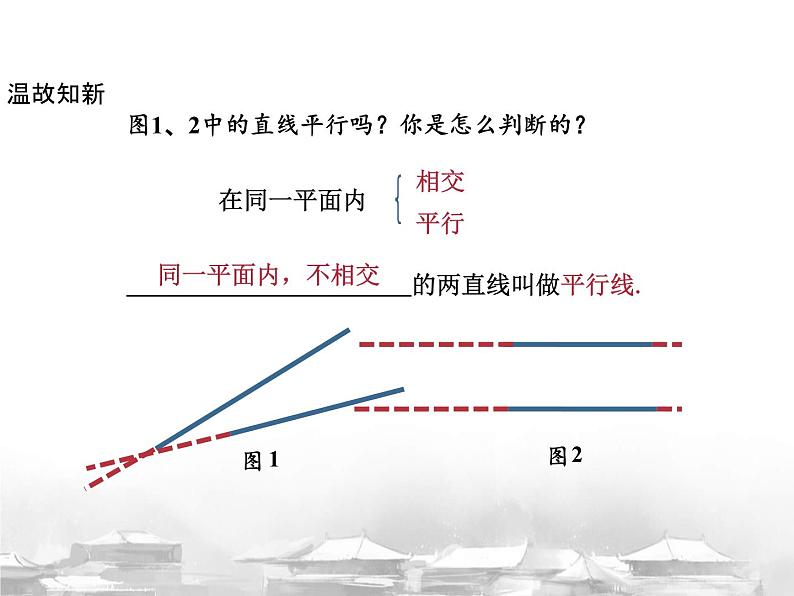
的两直线叫做平行线.
图1、2中的直线平行吗？你是怎么判断的？
除应用以上两种方法以外，是否还有其它方法呢？
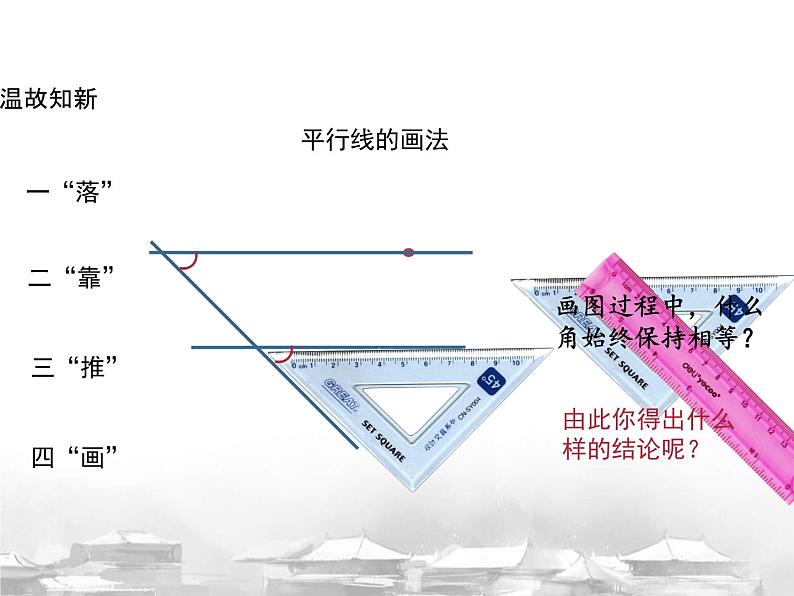
画图过程中，什么角始终保持相等？
由此你得出什么样的结论呢？
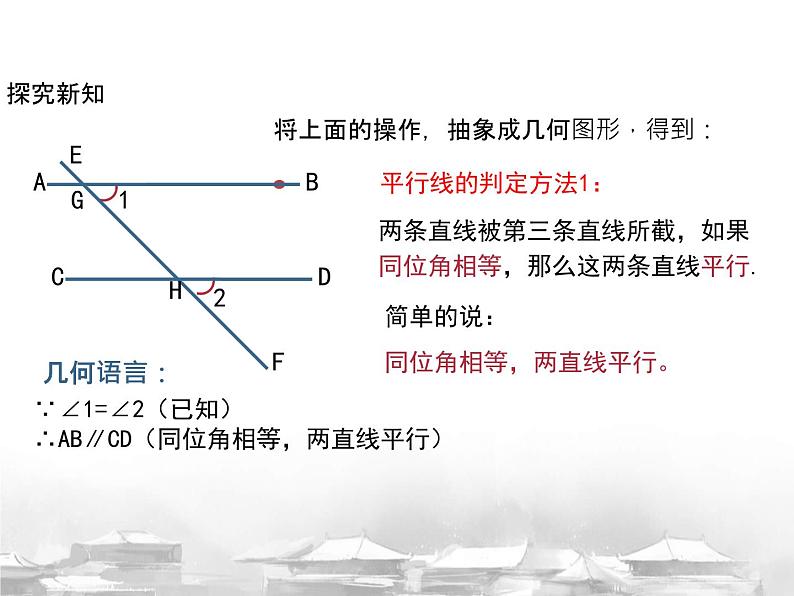
将上面的操作，抽象成几何图形，得到：
两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行.
同位角相等，两直线平行。
∵∠1=∠2（已知）∴AB∥CD（同位角相等，两直线平行）
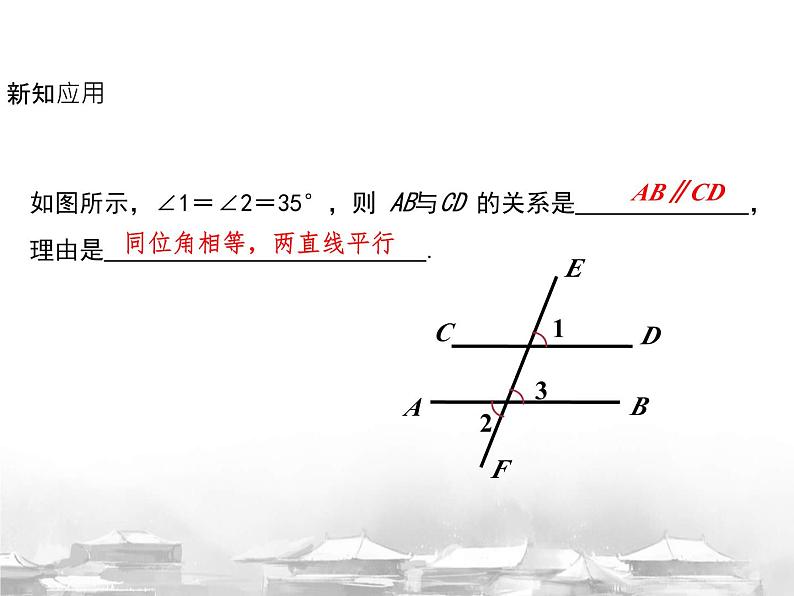
如图所示，∠1＝∠2＝35°，则 AB与CD 的关系是 ， 理由是 .
同位角相等，两直线平行
同位角相等，两直线平行.
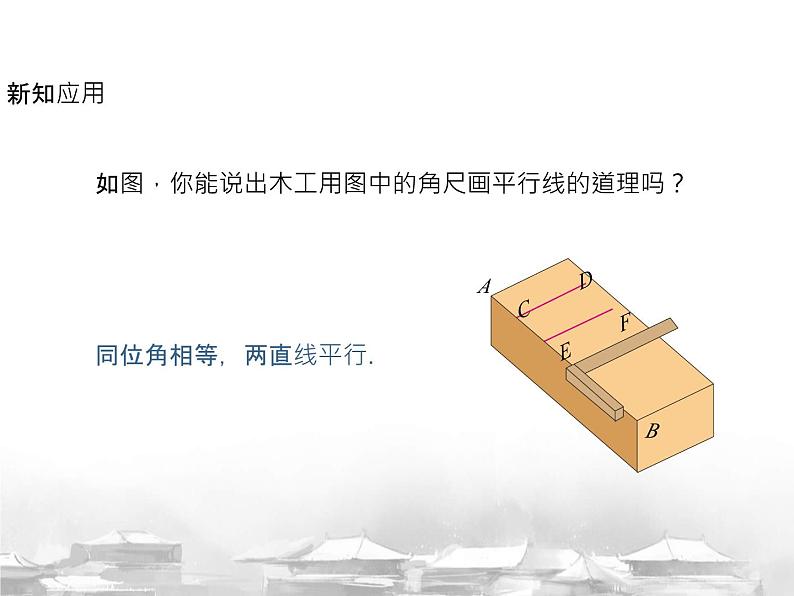
如图，你能说出木工用图中的角尺画平行线的道理吗？
由同位角相等可以判定两直线平行，能否利用内错角来判定两直线平行呢？
如图，已知3=2，求证：a//b。
解： ∵ 2=3(已知）， 3=1（ ）， ∴ 1=2. ∴ a//b( ）.
简单说成：内错角相等，两直线平行.
两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
∵∠3=∠2（已知）∴a∥b（内错角相等，两直线平行）
例：完成下面证明：如图所示，CB平分∠ACD，∠1＝∠3. 求证：AB∥CD. 证明：∵CB平分∠ACD，∴∠1＝∠2( _______).∵∠1＝∠3，∴∠2＝∠ . ∴AB∥CD(_______________________).
内错角相等，两直线平行
如图，如果∠1+∠2＝180º ，你能判定AB∥CD吗?
答:能。理由如下：∵1+2=180°（已知） 1+3=180°（邻补角的性质）∴2=3（同角的补角相等）∴AB//CD（内错角相等，两直线平行）
两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成：同旁内角互补，两直线平行.
∵∠1+∠2=180º（已知）∴AB∥CD（同旁内角互补， 两直线平行）
1.画AB平行于CD，实际上是画∠1等于∠2，这两个角是什么关系？
两条直线被第三条直线所截，如果______ 相等，那么这两条直线 .
同位角相等, 两直线平行.
你能说出木工用下图中的角尺画平行线的道理吗？
例 如图，b⊥a， c⊥a，直线b ，c平行吗？
∵ b⊥a， c⊥a，∴∠1=∠2 = 90°.∴b ∥ c（同位角相等，两直线平行）.
结论：垂直于同一条直线的两条直线互相（ ）.
两条直线被第三条直线所截，形成的角中，有同位角、内错角和同旁内角，同位角相等, 两直线平行，那么，利用内错角、同旁内角的关系，能否判定两直线平行？
∠ 1= ∠ 3 （对顶角相等），
∴ ∠1= ∠2 （等量代换），
∴ a∥b (同位角相等，两直线平行）.
问题1：当∠2 =∠3时，直线a，b是什么关系？为什么？
两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
内错角相等，两直线平行.
问题2：你能发现当∠2 ，∠4有怎样的关系时，直线a∥b吗？
讨论：如果∠2+∠4= 180°，能得到 a∥b吗?
∵ ∠1 + ∠4= 180°，∠2 + ∠4 = 180°，∴ ∠1 =∠2（同角的补角相等），∴ a∥b (同位角相等，两直线平行）.
同旁内角互补，两直线平行.
两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.
想一想，我们是怎样利用“同位角相等, 两直线平行”得到“内错角相等，两直线平行”和“同旁内角互补，两直线平行”的.
例 如图：直线AB、CD与AE相交，且∠1+∠A=180º ．求证：AB//CD
∠1=∠2 （ ）
同旁内角互补，两直线平行
例：在同一平面内，如果两条直线都垂直于同一条直线， 那么两条直线平行吗？为什么？
已知：直线b⊥a，c⊥a .求证： b∥c
∵b⊥a，c⊥a( )
∴∠1＝∠2＝90º( )
∴b∥c( )
③ ∵∠4 +∠ 5= 180º（已知） ∴ AB∥CD ( )
② ∵∠3 = ∠ 5（已知） ∴ AB∥CD ( )
① ∵∠2 = ∠ 6（已知） ∴ AB∥CD ( )
1.如图,可以确定AB∥CE的条件是( )A.∠2=∠B；B. ∠1=∠A；C. ∠3=∠B；D. ∠3=∠A
2.如图,已知∠1=30°,∠2或∠3满足条件_________ _ _，则a//b.
∠2＝150°或∠3＝30°
① ∵ ∠1 =_____（已知） ∴ AB∥CE( )
② ∵ ∠1 +_____=180（已知） ∴CD∥BF( )
③ ∵ ∠1 +∠5 =180（已知） ∴ ___∥_____( )
④ ∵ ∠4 +_____=180（已知） ∴ CE∥AB( )
内错角相等,两直线平行
同旁内角互补,两直线平行
3.根据条件完成填空.
答： AB∥CD .理由如下：∵ AC平分∠BAD∴ ∠1=∠3 ∵ ∠1=∠2∴ ∠2=∠3 ∴ AB∥CD（内错角相等，两直线平行）.
4、已知：如图，四边形ABCD中，AC平分∠BAD， ∠1=∠2，AB与CD平行吗？为什么？
5.如图所示，木工师傅在一块木板上画两条平行线，方法是：用角尺画木板边缘的两条垂线，这样画的理由有下列4种说法：其中正确的是( )①同位角相等，两直线平行；②内错角相等，两直线平行；③同旁内角互补，两直线平行；④平面内垂直于同一直线的两条 直线平行. A. ①②③ B.①②④ C. ①③④ D.①③
你能用判定方法2解决这个问题吗？
解：∵b⊥a，c⊥a，∴∠1=90°，∠3=90° ，∴∠1=∠3， ∴b∥c（内错角相等，两直线平行）.
你能用判定方法3解决这个问题吗？
解：∵b⊥a，c⊥a，∴ ∠1=90°，∠3=90° ，∴ ∠1+∠3=180°， ∴b∥c（同旁内角互补，两直线平行）.
1.如图，BE是AB的延长线. （1）由∠CBE=∠A可以判定哪两条直线平行？根据是什么？ （2）由∠CBE=∠C可以判定哪两条直线平行？根据是什么？
解：（1）由∠CBE=∠A可以判断AD∥BC，根据是同位角相等，两条直线平行.
解：（2）由∠CBE=∠C可以判断CD∥AE，根据是内错角相等，两条直线平行．
2.在铺设铁轨时，两条直轨必须是互相平行的.如图，已经知道∠2是直角，那么再度量图中已标出的哪个角，就可以判断两条直轨是否平行？为什么？
解：①通过度量∠3的度数，若满足∠2+∠3=180°，根据同旁内角互补，两直线平行，就可以验证这个结论；②通过度量∠4的度数，若满足∠2=∠4，根据同位角相等，两直线平行，就可以验证这个结论；③通过度量∠5的度数，若满足∠2=∠5，根据内错角相等，两直线平行，就可以验证这个结论．
3.如图，这是小明同学自己制作的英语抄写纸的一部分.其中的横格线互相平行吗？你有多少种判别方法？
解：横格线互相平行．判断方法有：画一条直线与横格线相交，然后利用同位角相等判断横格线平行；或利用内错角相等判断横格线平行；或利用同旁内角互补判断横格线平行等．
4.有一块长方形的玻璃，你能用什么方法检查它的对边是平行的？
解：可以通过测量玻璃的四个角，看相邻两个角的和是否为180°，若是，就平行．