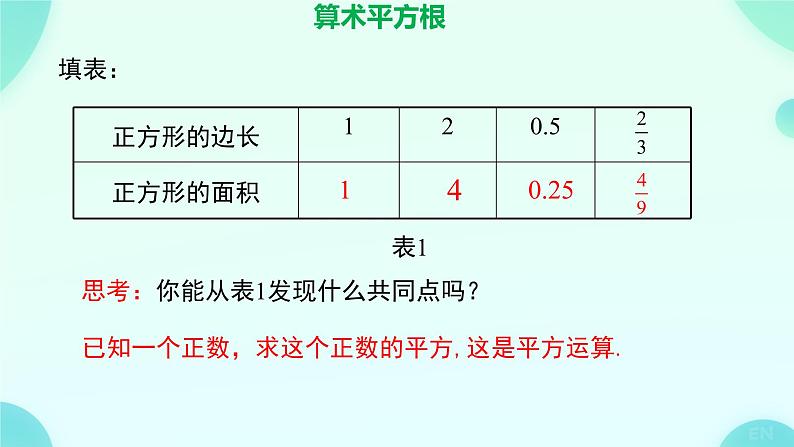
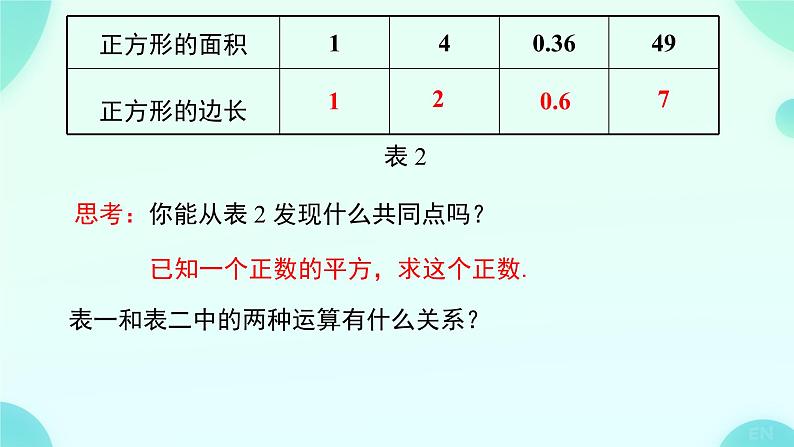
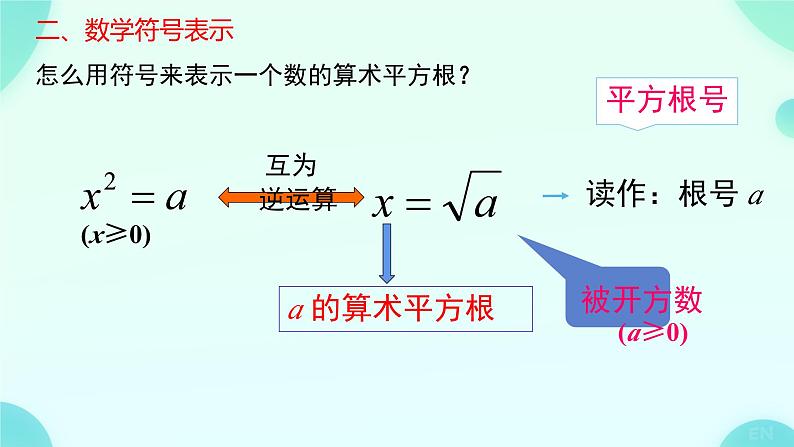
初中数学人教版（2024）七年级下册（2024）第八章 实数8.1 平方根课文内容课件ppt

这是一份初中数学人教版（2024）七年级下册（2024）第八章 实数8.1 平方根课文内容课件ppt，共30页。PPT课件主要包含了学习目标等内容，欢迎下载使用。
1.了解算术平方根的概念，会用根号表示一个数的算 术平方根;（重点）2.会求非负数的算术平方根，掌握算术平方根的非负 性．（重点、难点）
被开方数 (a≥0)
1.填空：（看谁算得又对又快） (1) 一个数的算术平方根是3，则这个数是 . (2) 一个自然数的算术平方根为a，则这个自然数 是___；和这个自然数相邻的下一个自然数是 . (3) 的算术平方根为 . (4) 2的算术平方根为____.
2.求下列各数的算术平方根:（1）169； (2) ； (3) 0.0001.
3.下列式子表示什么意义？你能求出它们的值吗？
解:设每块地板砖的边长为x m.由题意得故每块地板砖的边长是0.5 m.
4.用大小完全相同的240块正方形地板砖，铺一间面积为60 m2的会议室的地面，每块地板砖的边长是多少？
下列各式中哪些有意义？哪些无意义？为什么？
注意：被开方数为非负数.
1.填空：（看谁算得又对又快）(1) 一个数的算术平方根是3，则这个数是 .(2) 一个自然数的算术平方根为a，则这个自然数是___；和这个自然数相邻的下一个自然数是 . (3) 的算术平方根为 .(4) 2的算术平方根为____.
2.求下列各数的算术平方根:（1）169； (2) ； (3) 0.0001.
解：（1）16 ； （2）3.
（1）本节课你学习了哪些知识？
（2）在探索知识的过程中，你积累了哪些经验？
这节课主要学习了算术平方根的概念和表示方法,知道了求一个正数的算术平方根与求一个正数的二次幂正好是互逆的过程，因此，求正数的算术平方根实际上可以转化为求一个数的二次幂运算. 只不过，只有正数和0才有算术平方根.
思维方法：求一个正数的算术平方根运算和开平方求一个正数的二次幂运算互为逆运算.探究策略：由特殊到一般，再由一般到特殊，是发现问题和解决 问题的基本方法和途径.
已知：｜x+2y|+
求x-3y+4z的值.