2024年浙江省金华市中考数学模拟试卷（原卷版）

这是一份2024年浙江省金华市中考数学模拟试卷（原卷版），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
说明：本卷共有1大题，10小题．
一、选择题（本题有10小题）
1. 在中，是无理数的是（ ）
A. B. C. D. 2
2. 计算的结果是（ ）
A. aB. C. D.
3. 体现我国先进核电技术的“华龙一号”，年发电能力相当于减少二氧化碳排放16320000吨，数16320000用科学记数法表示为（ ）
A. B. C. D.
4. 已知三角形两边长分别为和，则第三边的长可以是（ ）
A. B. C. D.
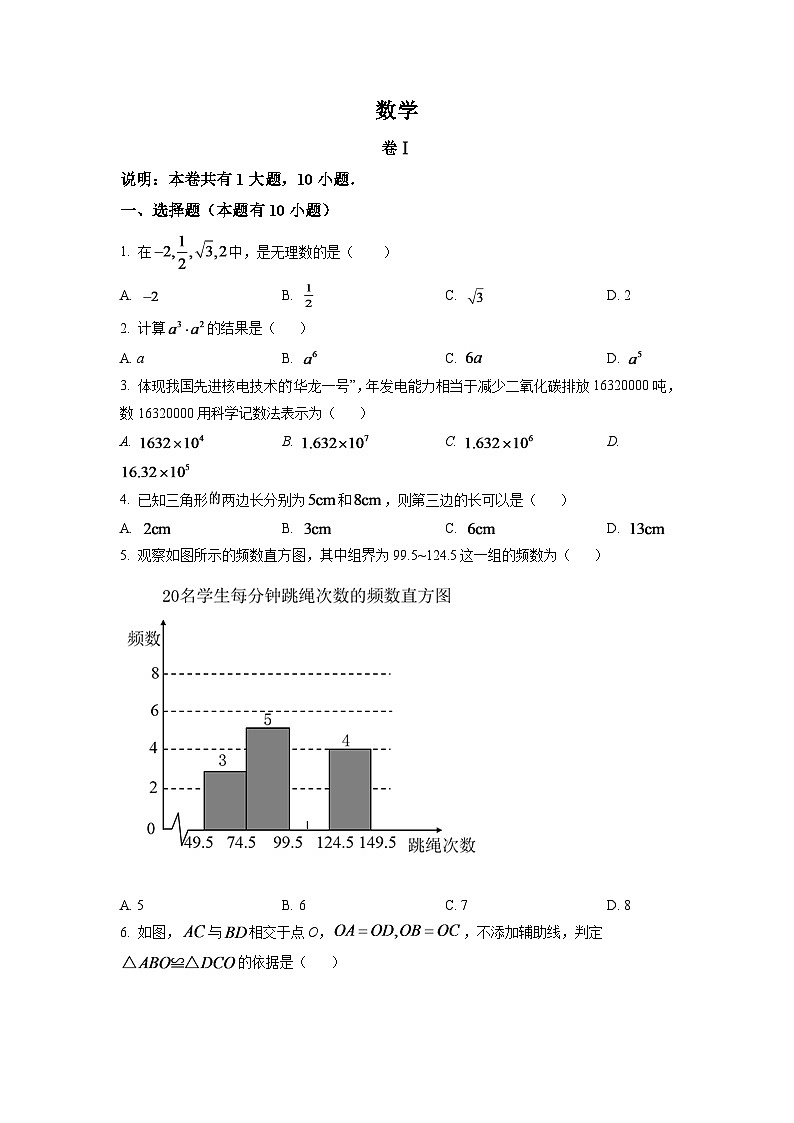
5. 观察如图所示的频数直方图，其中组界为99.5~124.5这一组的频数为（ ）
A. 5B. 6C. 7D. 8
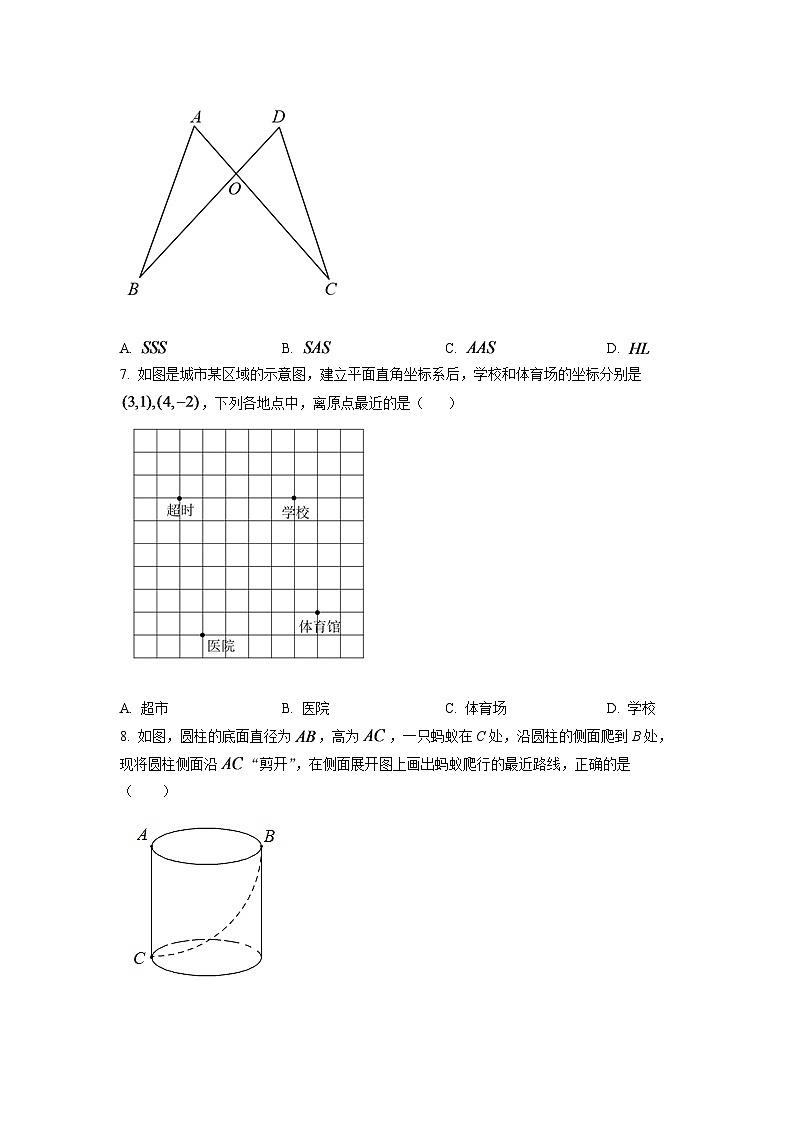
6. 如图，与相交于点O，，不添加辅助线，判定的依据是（ ）
A. B. C. D.
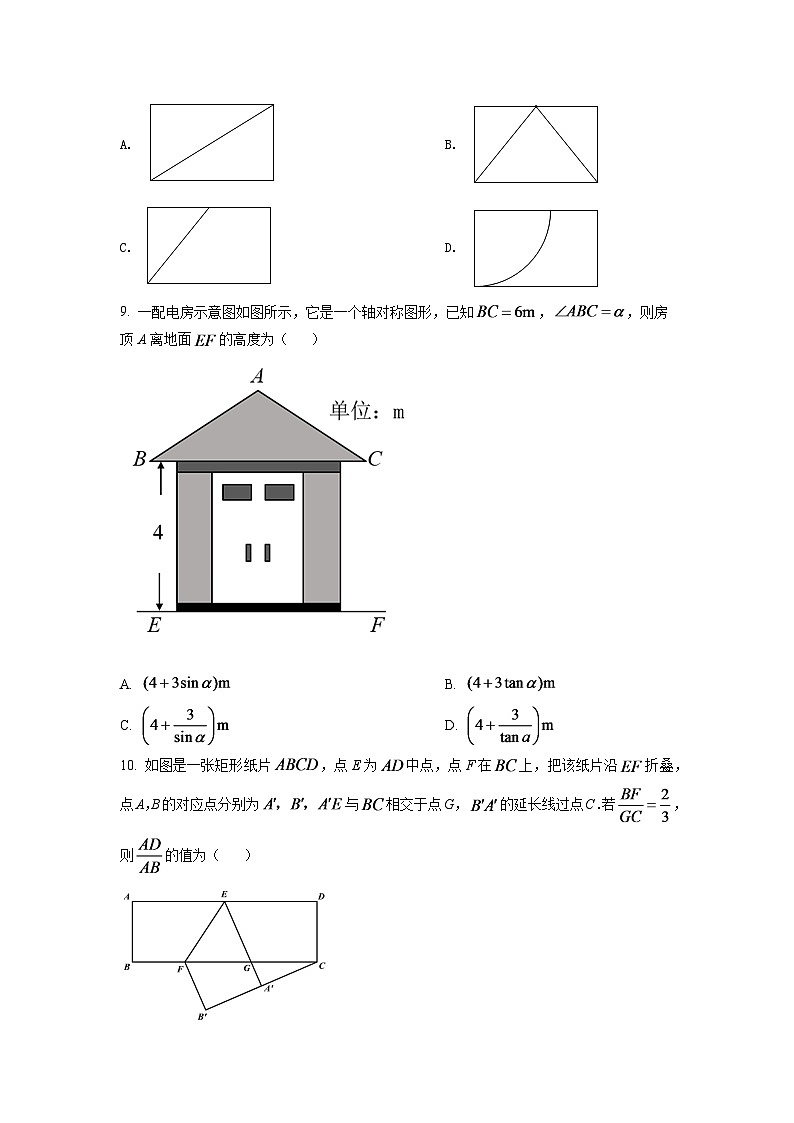
7. 如图是城市某区域的示意图，建立平面直角坐标系后，学校和体育场的坐标分别是，下列各地点中，离原点最近的是（ ）
A. 超市B. 医院C. 体育场D. 学校
8. 如图，圆柱的底面直径为，高为，一只蚂蚁在C处，沿圆柱的侧面爬到B处，现将圆柱侧面沿“剪开”，在侧面展开图上画出蚂蚁爬行的最近路线，正确的是（ ）
A. B.
C. D.
9. 一配电房示意图如图所示，它是一个轴对称图形，已知，，则房顶A离地面的高度为（ ）
A. B.
C. D.
10. 如图是一张矩形纸片，点E为中点，点F在上，把该纸片沿折叠，点A，B的对应点分别为与相交于点G，的延长线过点C．若，则的值为（ ）
A. B. C. D.
卷Ⅱ
说明：本卷共有2大题，14小题
二、填空题（本题有6小题）
11. 因式分解：______．
12. 若分式的值为2，则x的值是_______．
13. 一个布袋里装有7个红球、3个白球，它们除颜色外都相同．从中任意摸出1个球，摸到红球的概率是______．
14. 如图，在中，．把沿方向平移，得到，连结，则四边形的周长为_____．
15. 如图，木工用角尺的短边紧靠⊙于点A，长边与⊙相切于点B，角尺的直角顶点为C，已知，则⊙的半径为_____．
16. 图1是光伏发电场景，其示意图如图2，为吸热塔，在地平线上的点B，处各安装定日镜（介绍见图3）．绕各中心点旋转镜面，使过中心点的太阳光线经镜面反射后到达吸热器点F处．已知，在点A观测点F的仰角为．
（1）点F的高度为______m．
（2）设，则与的数量关系是_______．
三、解答题（本题有8小题，各小题都必须写出解答过程）
17. 计算：．
18. 解不等式：．
19. 如图1，将长为，宽为矩形分割成四个全等的直角三角形，拼成“赵爽弦图”（如图2），得到大小两个正方形．
（1）用关于a的代数式表示图2中小正方形的边长．
（2）当时，该小正方形的面积是多少？
20. 如图，点A在第一象限内，轴于点B，反比例函数的图象分别交于点C，D．已知点C的坐标为．
（1）求k的值及点D的坐标．
（2）已知点P在该反比例函数图象上，且在的内部（包括边界），直接写出点P的横坐标x的取值范围．
21. 学校举办演讲比赛，总评成绩由“内容、表达、风度、印象”四部分组成．九（1）班组织选拔赛，制定的各部分所占比例如图，三位同学的成绩如表．请解答下列问题：
演讲总评成绩各部分所占比例的统计图：
三位同学的成绩统计表：
（1）求图中表示“内容”的扇形的圆心角度数．
（2）求表中m的值，并根据总评成绩确定三人的排名顺序．
（3）学校要求“内容”比“表达”重要，该统计图中各部分所占比例是否合理？如果不合理，如何调整？
22. 如图1，正五边形内接于⊙，阅读以下作图过程，并回答下列问题，作法：如图2，①作直径；②以F为圆心，为半径作圆弧，与⊙交于点M，N；③连接．
（1）求的度数．
（2）是正三角形吗？请说明理由．
（3）从点A开始，以长为半径，在⊙上依次截取点，再依次连接这些分点，得到正n边形，求n的值．
23. “八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：①统计售价与需求量的数据，通过描点（图1），发现该蔬菜需求量（吨）关于售价x（元/千克）的函数图象可以看成抛物线，其表达式为，部分对应值如表：
②该蔬菜供给量（吨）关于售价x（元/千克）的函数表达式为，函数图象见图1．
③1~7月份该蔬菜售价（元/千克），成本（元/千克）关于月份t函数表达式分别为，，函数图象见图2．
请解答下列问题：
（1）求a，c的值．
（2）根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由．
（3）求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润．
24. 如图，在菱形中，，点E从点B出发沿折线向终点D运动．过点E作点E所在的边（或）的垂线，交菱形其它的边于点F，在的右侧作矩形．
（1）如图1，点G上．求证：．
（2）若，当过中点时，求的长．
（3）已知，设点E的运动路程为s．当s满足什么条件时，以G，C，H为顶点的三角形与相似（包括全等）？内容
表达
风度
印象
总评成绩
小明
8
7
8
8
m
小亮
7
8
8
9
7.85
小田
7
9
7
7
7.8
售价x（元/千克）
…
2.5
3
3.5
4
…
需求量（吨）
…
7.75
7.2
6.55
58
…