2025年九年级中考数学二轮专题复习 平行线性质与判定的综合运用 课件

这是一份2025年九年级中考数学二轮专题复习 平行线性质与判定的综合运用 课件，共34页。PPT课件主要包含了对应练习，探究提升，课堂训练，课后提高等内容，欢迎下载使用。
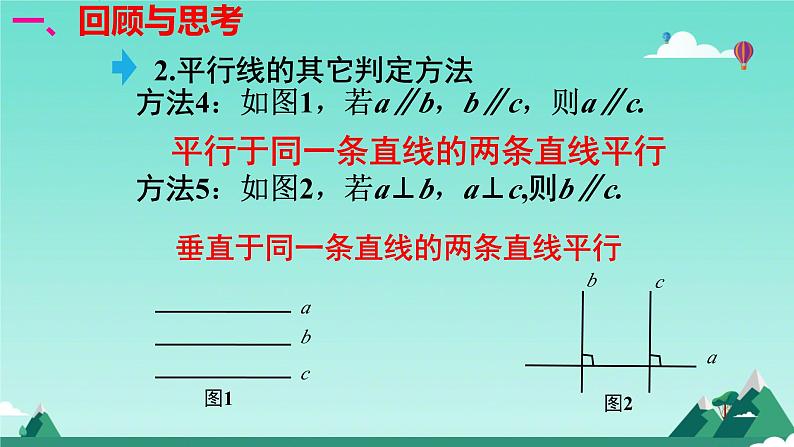
方法4：如图1，若a∥b，b∥c，则a∥c. 方法5：如图2，若a⊥b，a⊥c,则b∥c.
平行于同一条直线的两条直线平行
垂直于同一条直线的两条直线平行
2.平行线的其它判定方法
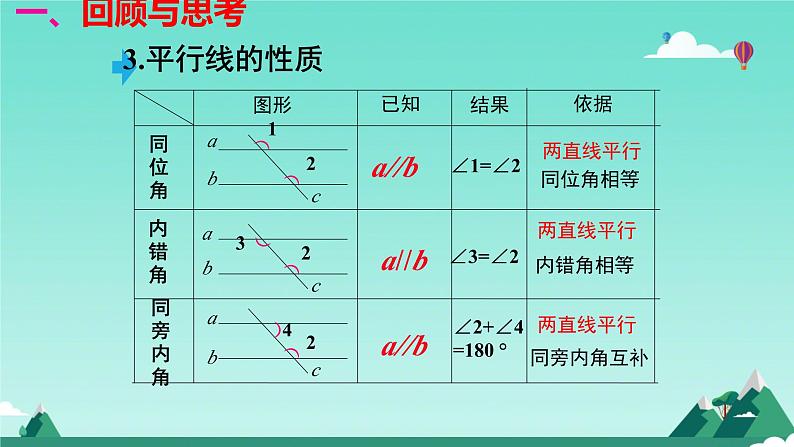
∠2+∠4=180 °
平行线的判定和性质回顾
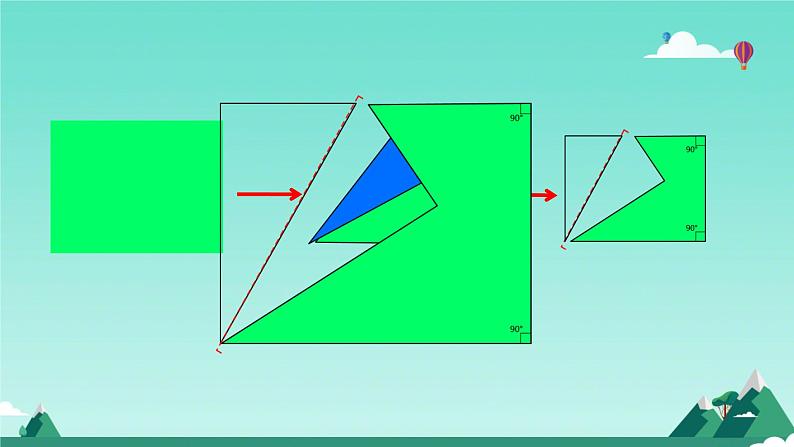
将一张长方形纸片沿一个角的顶点折叠，折叠后的两个角和是多少度？
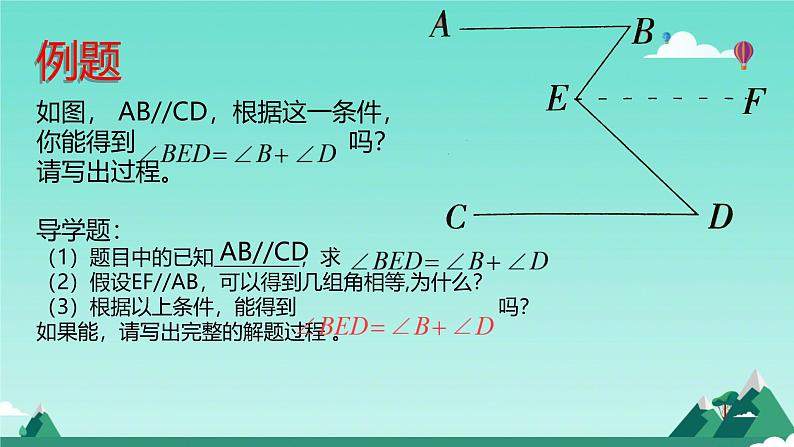
如图， AB//CD，根据这一条件，你能得到 吗？请写出过程。
导学题：（1）题目中的已知 ，求（2）假设EF//AB，可以得到几组角相等,为什么？（3）根据以上条件，能得到 吗？如果能，请写出完整的解题过程 。
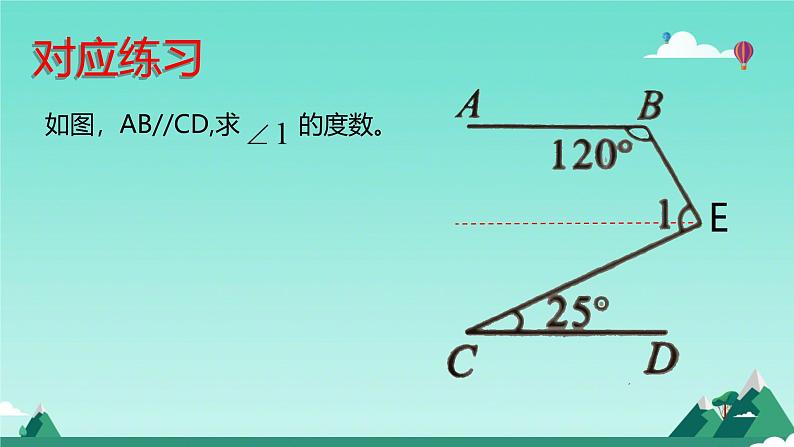
如图，AB//CD,求 的度数。
如图,已知AB//CD,试求
（1） 的度数（2） 的度数（3） 的度数（4） 的度数
1.如图一、点F,E分别在线段AB和CD上，下列条件能判定AB//CD的是 ( ) A .∠1=∠4 B.∠1=∠2 C.∠4=∠2 D.∠3=∠4
3.如图三、AB//CD,点E在AB上,点F在CD上，如果∠CFE : ∠EFB=3 : 4， ∠ABF=400，求∠BEF的度数。
2.如图二、直线AB//CD, ∠C=440,∠E为直角，∠1=
(1) ∵ ∠1 =_____（已知）∴AB∥CE （ ）
(2) ∵ ∠1 +_____=180（已知） ∴ CD∥BF( )
内错角相等,两直线平行
（ ）
两直线平行，同旁内角互补
同旁内角互补,两直线平行
两直线平行，同位角相等
合作探究 如图，AB∥CD，如果∠1=∠2，那么EF与AB平行吗？说说你的理由．
如图，已知
证明：∵AB∥CD ∴∠BAD=∠CAD（两直线平行，内错角相等）
∵∠1=∠2（已知）∴∠3=∠4（等式的性质）
∴AF∥DE（内错角相等，两直线平行）
∴∠E=∠F（两直线平行，内错角相等）
1、点D,E,F分别是三角形ABC的边 BC、CA、AB上的点，DE∥BA,DF∥CA.求证∠FDE=∠A.
两直线平行，内错角相等
( )
2、AB和CD相交于点O,∠C=∠COA，∠D=∠BOD.求证：AC∥BD.
( )

( )
内错角相等，两直线平行
平行线中的拐点问题 四种模型
已知AB∥CD，∠1，∠2，∠BED 间有怎样的数量关系？
过点E 作MN∥AB,
∵ MN∥AB, AB∥CD,
∴ MN∥CD.(同平行于一直线的两直线相互平行）
又∵ ∠3+∠4=∠BED,
∴ ∠1+∠2=∠BED.
∴ ∠1=∠3.（两直线平行，内错角相等)
∴ ∠2=∠4.（两直线平行，内错角相等)
解：过点E 作MN∥AB,
已知AB∥CD，∠1，∠2，∠AEC 间有怎样的数量关系？
又∵ ∠3+∠4=∠AEC,
∴ ∠1+∠2+∠AEC=360°.
∴ ∠1+∠3=180°.（两直线平行，同旁内角互补）
∴ ∠2+∠4=180°.（两直线平行，同旁内角互补）
已知AB∥CD，∠1，∠2，∠3 间有怎样的数量关系？
过点E 作EF∥AB,
∵ EF∥AB, AB∥CD,
∴ EF∥CD.(同平行于一直线的两直线相互平行）
∴ ∠1-∠2-∠3=0,
∴ ∠1=∠2+∠3.
∴ ∠1+∠4=180°.（两直线平行，同旁内角互补）
∴ ∠2+∠4+∠3=180°.
解：过点E 作EF∥AB,
∴ EF∥CD.（同平行于一直线的两直线相互平行）
∴ ∠3 =∠4 (两直线平行，内错角相等）
∴ ∠2+∠4 =∠1.(两直线平行，内错角相等）
1 如图，a∥b,∠1=100°，∠3=60°，则∠2的度数为（ ）
A.120° B.130° C.140° D.150°
2 如图，AB∥CD,∠ABE和CDE的角平分线相交于F,∠E=60°， 则∠BFD的度数为（ ）
A.120° B.130° C.140° D.150°
3 如图，直线EF∥GH,，点A在EF上，AC交GH于点B.若∠EAC=100°， ∠ACD=58°，点D在GH上，则∠BDC的度数为 .
4.如图，AB//CD,求 的度数。
(1)如图1,∠1=72°,∠2=72°,∠3=60°,求∠4的度数为
（2）如图2 ，已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= °
（3）如图3,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( ) A.75° B.45° C.30° D.15°
证明：过点E作EF∥AB
∵AB∥CD∴EF∥CD（平行于同一直线的两直线平行）
∴ ∠B=∠3，∠4=∠D（两直线平行，内错角相等）
∵ ∠1=∠B，∠2=∠D（已知）∴ ∠1=∠3，∠2=∠4 （等量代换）
∵ ∠1+∠3+∠4+∠2=180°∴2∠3+2∠4=180°∴∠3+∠4=90°
即 ∠BED=90°∴BE⊥DE