初中数学沪科版（2024）七年级下册（2024）10.2 平行线的判定多媒体教学课件ppt

这是一份初中数学沪科版（2024）七年级下册（2024）10.2 平行线的判定多媒体教学课件ppt，共20页。PPT课件主要包含了学习目标，复习回顾，探究新知，符号语言，平行线的判定方法2，你能证明这个猜想吗，平行线的判定方法3，①②④，∠1∠4，∠2∠4等内容，欢迎下载使用。
1.能用平行线的判定方法1推理出后两种判定方法.
2.能运用平行线的判定方法对两条直线的位置关系进行简单的推理.
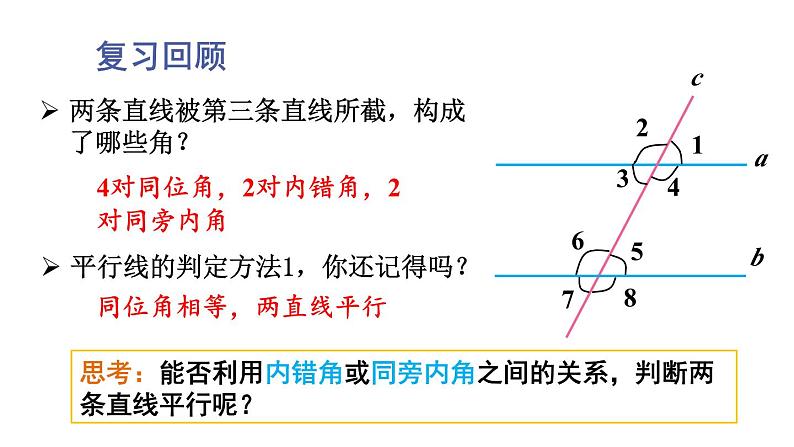
两条直线被第三条直线所截，构成了哪些角？
4对同位角，2对内错角，2对同旁内角
思考：能否利用内错角或同旁内角之间的关系，判断两条直线平行呢？
平行线的判定方法1，你还记得吗？
同位角相等，两直线平行
探究1：如图，直线a，b被直线c所截，如果内错角∠2=∠4，你能说明直线a∥b吗？
解： 因为 2=4 (已知) ，2=1 (对顶角相等) ，所以 1=4.所以 a∥b (同位角相等，两直线平行) .
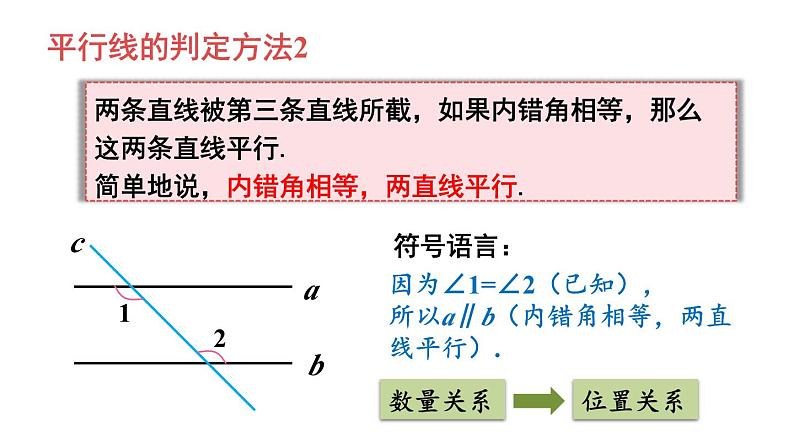
因为∠1=∠2（已知），所以a∥b（内错角相等，两直线平行）.
两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.简单地说，内错角相等，两直线平行.
【选自教材P142练习第1题】
练习1 如图，如果∠1=47°，∠2=47°，∠3=47°，可以判定哪些直线平行？判定的依据分别是什么？
解：因为∠1=∠2=47°，所以 BC∥DE.依据：内错角相等，两直线平行.因为∠2=∠3=47°，所以AB∥EF.依据：同位角相等，两直线平行.
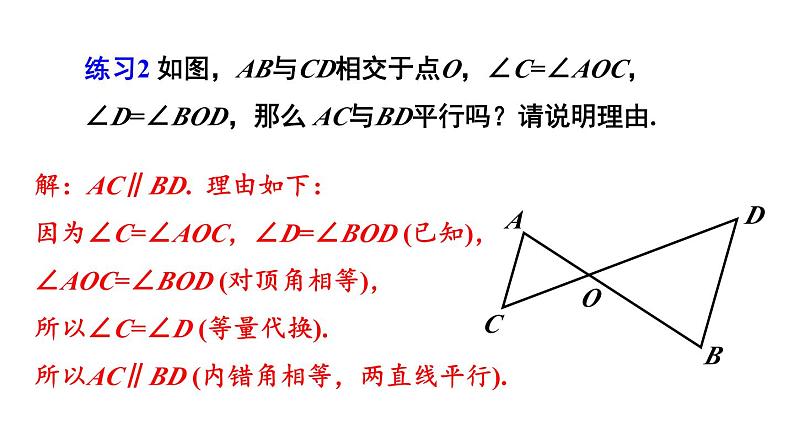
练习2 如图，AB与CD相交于点O，∠C=∠AOC，∠D=∠BOD，那么 AC与BD平行吗？请说明理由.
解：AC∥BD. 理由如下：因为∠C=∠AOC，∠D=∠BOD (已知)，∠AOC=∠BOD (对顶角相等)，所以∠C=∠D (等量代换).所以AC∥BD (内错角相等，两直线平行).
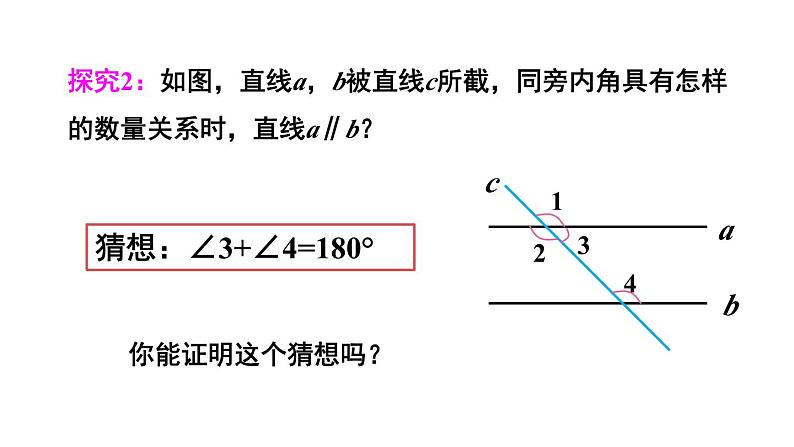
探究2：如图，直线a，b被直线c所截，同旁内角具有怎样的数量关系时，直线a∥b？
猜想：∠3+∠4=180°
解：因为3+4=180° (已知) ，3+1=180° (平角的定义) ，所以1=4 (同角的补角相等) .所以a∥b (同位角相等，两直线平行) .
还有没有其他的证明方法？
解：因为3+4=180° (已知) ，3+2=180° (平角的定义) ，所以2=4 (同角的补角相等) .所以a∥b (内错角相等，两直线平行) .
因为∠1+∠2=180°（已知），所以a∥b（同旁内角互补，两直线平行）.
两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.简单地说，同旁内角互补，两直线平行.
【选自教材P142练习第2题】
练习3 如图，若∠A=62°，∠B=118°，可以判定哪两条直线平行？判定的依据是什么？
解：因为∠A+∠B=62°+118°=180°，所以 AD∥BC.依据：同旁内角互补，两直线平行.
练习4 如图，下列推理中正确的是________.（填序号）①因为∠B=∠BEF，所以AB∥EF；②因为∠B=∠CDE，所以AB∥CD；③因为∠DCE+∠AEF=180°，所以AB∥EF；④因为∠A+∠AEF=180°，所以AB∥EF.
归纳：平行线的判定方法
1.如图，在下列给出的条件中，不能判定AB∥DF 的是（ ）A.∠A+∠2=180°B.∠1=∠AC.∠1=∠4D.∠A=∠3
2.完成下面的说理过程，并在括号中填上适当的理由.如图，在三角形ABC中，CD⊥AB于点D，E是AC上一点，且∠1+∠2=90°. 试说明：DE∥BC.解：因为CD⊥AB（已知），所以∠1+________=90°（ ）.因为∠1+∠2=90°（已知），所以________=∠2（ ）.所以DE∥BC（ ）.
内错角相等，两直线平行
3.如图，AB⊥BD于点B，CD⊥BD于点D，∠1+∠2=180°，CD与EF平行吗？为什么？
解：CD∥EF. 理由如下：因为AB⊥BD，CD⊥BD（已知），所以∠B=∠D=90°（垂直的定义）.所以∠B+∠D=180°（等式的基本性质）.所以AB∥CD（同旁内角互补，两直线平行）.因为∠1+∠2=180°（已知），所以AB∥EF（同旁内角互补，两直线平行）.所以CD∥EF（如果两条直线和第三条直线平行，那么这两条直线平行）.
4.如图，∠ADE+∠BCF=180°，BE平分∠ABC，∠ABC=2∠E.（1）AD与BC平行吗？为什么？
解：AD∥BC. 理由如下：因为∠ADE+∠ADF=180°（平角的定义），∠ADE+∠BCF=180°（已知），所以∠ADF=∠BCF（等量代换）.所以AD∥BC（同位角相等，两直线平行）.
（2）AB与EF的位置关系如何？为什么？
解：AB∥EF. 理由如下：因为BE平分∠ABC，所以∠ABE= ∠ABC（角平分线的定义）.又∠ABC= 2∠E（已知），即∠E= ∠ABC（等式的性质），所以∠ABE=∠E（等量代换）.所以AB∥EF（内错角相等，两直线平行）.