2025高考数学二轮复习-微专题22-数列中的最值、范围问题【课件】

这是一份2025高考数学二轮复习-微专题22-数列中的最值、范围问题【课件】，共59页。PPT课件主要包含了真题体验，热点突破，精准强化练等内容，欢迎下载使用。
近几年高考试题中，与数列有关的最值范围问题既有解答题，也有选择、填空题，难度中档或偏上.
1.(2024·上海卷)等比数列{an}的首项a1>0，公比q>1，记In＝{x－y|x，y∈[a1，a2]∪ [an，an＋1]}，若对任意正整数n，In是闭区间，则q的取值范围是___________.
显然等比数列{an}递增，不妨设x≥y，若x，y∈[a1，a2]，则x－y∈[0，a2－a1]，若x，y∈[an，an＋1]，则x－y∈[0，an＋1－an]，若x∈[an，an＋1]，y∈[a1，a2]，则x－y∈[an－a2，an＋1－a1]，∵对任意正整数n，In都是闭区间，
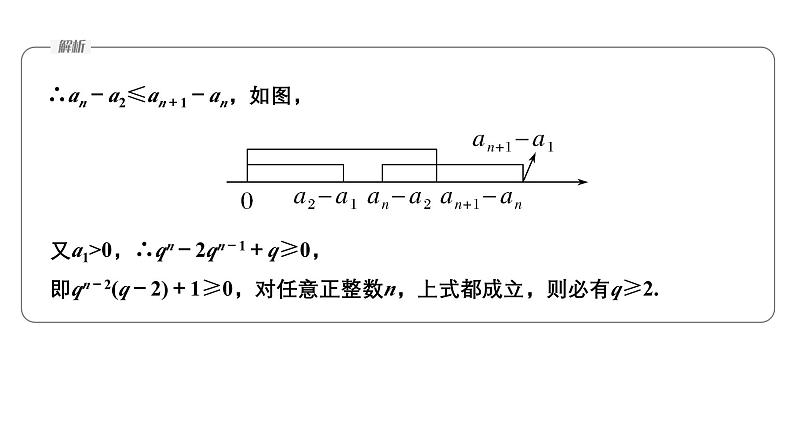
∴an－a2≤an＋1－an，如图，
又a1>0，∴qn－2qn－1＋q≥0，即qn－2(q－2)＋1≥0，对任意正整数n，上式都成立，则必有q≥2.
(2)设数列{bn}满足3bn＋(n－4)an＝0(n∈N*)，记{bn}的前n项和为Tn.若Tn≤λbn对任意n∈N*恒成立，求实数λ的取值范围.
热点一　求数列和式的最值、范围
热点二　求n的最值或范围
热点三　求数列不等式中参数的取值范围
利用数列和式的单调性求其最值.要首先判断其单调性，且注意数列中的n≥1且n∈N.
热点二　求n的最值或范围
求n的值或最值，一般涉及数列的项或和的最值与范围，通常化归为解关于n的不等式，或根据数列的单调性求解.
已知数列{an}是递增的等比数列.设其公比为q，前n项和为Sn，且满足a1＋a5＝34，8是a2与a4的等比中项.(1)求数列{an}的通项公式；
因为8是a2与a4的等比中项，所以a2a4＝82＝64，
由(1)得bn＝n·an＝n×2n，则Tn＝b1＋b2＋b3＋…＋bn＝1×21＋2×22＋3×23＋…＋n×2n，①2Tn＝1×22＋2×23＋3×24＋…＋n×2n＋1，②由①－②得－Tn＝21＋22＋23＋…＋2n－n×2n＋1，
(2)若bn＝n·an，Tn是{bn}的前n项和，求使Tn－n·2n＋1>－100成立的最大正整数n的值.
由Tn－n·2n＋1>－100，得2－2n＋1>－100，即2n－100成立的最大正整数n的值为5.
解答本题要首先正确求出Tn，在求n的最值时要结合Tn－n·2n＋1的单调性，同时注意n∈N*求解.
(2)设数列{an}的前n项和为Sn，求当Sn＋2n＋1≥50时，正整数n的最小值.
此类问题以数列为载体，一般涉及数列的求和，考查不等式的恒成立问题，可转化为函数的最值问题.
求数列不等式中参数的取值范围问题要看清楚是恒成立，还是有解问题，若f(n)≥M恒成立，则f(n)min≥M；若f(n)≥M有解，则f(n)max≥M.
1.已知数列{an}是等比数列，若a9·a12>1，0