湖北省“新高考联考协作体”2024-2025学年高一上学期期末考试数学试卷（Word版附答案）

这是一份湖北省“新高考联考协作体”2024-2025学年高一上学期期末考试数学试卷（Word版附答案），共13页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
1.命题“，”的否定是( )
A. ，B. ，
C. ，D. ，
2.已知集合，，则( )
A. B. C. D.
3.已知，那么( )
A. B. C. D.
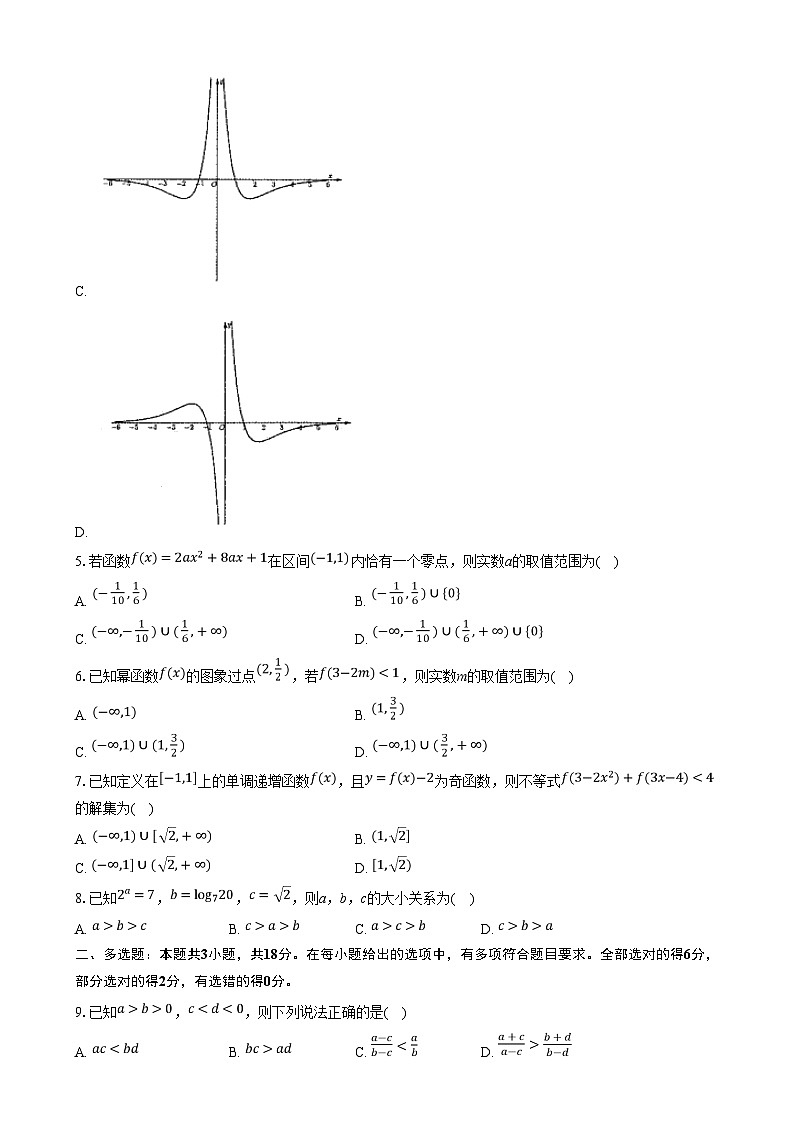
4.函数的图象大致是( )
A.
B.
C.
D.
5.若函数在区间内恰有一个零点，则实数a的取值范围为( )
A. B.
C. D.
6.已知幂函数的图象过点，若，则实数m的取值范围为( )
A. B.
C. D.
7.已知定义在上的单调递增函数，且为奇函数，则不等式的解集为( )
A. B.
C. D.
8.已知，，，则a，b，c的大小关系为( )
A. B. C. D.
二、多选题：本题共3小题，共18分。在每小题给出的选项中，有多项符合题目要求。全部选对的得6分，部分选对的得2分，有选错的得0分。
9.已知，，则下列说法正确的是( )
A. B. C. D.
10.已知函数的图象的一条对称轴方程为，下列说法正确的是( )
A. 函数的对称中心为
B. 不等式的解集为
C. 函数的单调递增区间为
D. 函数在区间上的值域为
11.下列说法正确的是( )
A. 当时，的最大值为
B. 当时，的最小值为3
C. 当，且时，的最小值为8
D. 当，且时，的最小值为5
三、填空题：本题共3小题，每小题5分，共15分。
12.计算： .
13.如图，已知扇形 AOB所在圆的半径为2，其圆心角为，若的面积为1，则该扇形的面积为 .
14.已知函数，若关于x的方程有6个不同的实根，则实数a的取值范围是 .
四、解答题：本题共5小题，共77分。解答应写出文字说明，证明过程或演算步骤。
15.本小题13分
已知集合，集合
当时，求
若“”是“”的充分不必要条件，求实数a的取值范围.
16.本小题15分
已知角的终边过点，且，求，的值;
已知角满足：，其中角为第三象限角，求的值.
17.本小题15分
湖北省孝感市孝昌县丰山镇将自身定位为“生态水果特色小镇”，这一举措充分展现了其对国家“强国必先强农，农强方能国强”号召的深刻理解与实践.通过这一发展战略，不仅促进了乡村产业的转型升级，还兼顾了生态环境保护，为乡村的全面振兴探索出了一条富有前瞻性和可持续性的道路.经调研发现：某珍稀水果树的单株产量单位：千克与施用肥料单位：千克满足如下关系：，肥料成本投入为5x元，其它成本投入如培育管理、施肥等人工费为10x元，且，
求实数a，b的值;
已知这种水果的市场售价大约为30元/千克，且销路畅通供不应求.记该水果树的单株利润为单位：元当施用肥料为多少千克时，该水果树的单株利润最大?最大利润是多少?
18.本小题17分
已知函数在区间上有且仅有4个零点.
求的取值范围;
当时，若不等式在区间上恒成立，求实数m的取值范围;
当时，若函数在区间内有两个不同的零点，求实数t的取值范围.
19.本小题17分
已知函数是定义在R上的奇函数.
求实数a，b的值;
判断并证明函数的单调性;
当时，不等式恒成立，求实数t的取值范围.
答案和解析
1.【答案】B
【解析】【分析】
本题考查命题的否定，全称量词命题与存在量词命题的否定关系，属于基础题．
直接利用全称量词命题的否定是存在量词命题写出结果即可．
【解答】
解：因为全称量词命题的否定是存在量词命题，
所以命题“，”的否定是：，
故选
2.【答案】C
【解析】【分析】
本题考查了集合的交运算，属于基础题.
先求出集合A，B，再由交集运算可得答案.
【解答】
解：因为，所以，即，所以
又因为可化为，解得，所以，
所以
故选
3.【答案】A
【解析】【分析】
本题主要考查的是诱导公式，属于基础题.
利用诱导公式化简求值即可.
【解答】
解：因为，
所以，
故选
4.【答案】A
【解析】【分析】
本题考查函数图像的识别，属于基础题.
利用函数的奇偶性和函数值的分布情况即可判断.
【解答】
解：因为函数，定义域为，
则，
所以函数为偶函数，排除B ，D
又当时，，而，，所以，则，则排除C，
故选
5.【答案】C
【解析】解：当时，不满足题意;
当时，是对称轴为的抛物线，
所以函数在区间内为单调函数，要使得函数在区间内恰有一个零点，需满足，即，解得或
故选
6.【答案】D
【解析】【分析】
本题主要考查的是求具体函数的解析式，利用幂函数的性质解不等式，分式不等式，属于中档题.
根据幂函数的概念求得解析式，再利用幂函数的性质解不等式即可.
【解答】
解：设，因为幂函数的图象过点，所以，即，所以，
于是不等式可转化为，即，
所以，即或，
故选
7.【答案】B
【解析】解：因为为奇函数，所以，即，
于是，不等式可转化为，
因为是定义在上的单调递增函数，所以，
解得：故选
8.【答案】A
【解析】【分析】
本题考查了比较大小，考查了推理能力与计算能力，属于基础题．
利用比差法比较大小即可.
【解答】
解：因为，所以，又因为，
所以，
所以
而，
所以，所以，故，
故选
9.【答案】AC
【解析】【分析】
本题考查不等式的性质和运用：比较大小，属于基础题.
对BD，利用特殊值法判定，对于A，利用不等式的性质判定，对于C，利用作差法即可判定.
【解答】
解：，，即为，即有，即，故A正确；
取，，，，则，故BD错误；
，故，故C正确
故选
10.【答案】BD
【解析】【分析】
本题考查正弦型函数的图象与性质，属于中档题.
【解答】
解：因为的图象的一条对称轴方程为，
所以，解得，因为，所以，所以，
A选项，令，解得，所以函数的对称中心为，故A错误;
B选项，令，即，所以，解得，故B正确;
C选项，令，解得，故C错误;
D选项，当时，，所以，所以，故D正确;
故本题正确答案为：B、
11.【答案】ACD
【解析】【分析】
本题考查基本不等式和对勾函数的性质，考查了计算能力，属于中档题.
对于A选项，利用对勾函数的单调性即可求得最大值.
对于B选项，，再利用基本不等式求最小值即可.
对于C选项，令，则，所以，所以x，2y可看作方程的两根，
所以，故求得最小值为8，故C正确.
对于D选项，令，，则，所以，再利用基本不等式求最小值即可.
【解答】
对于A，令，则，
在上单调递增，所以当时，取得最大值，故A正确;
对于B，当时，，
，当且仅当，时，等号成立，
故的最小值为，故B错误;
对于C，令，则，所以，所以x，2y可看作方程的两根，
所以，解得或舍去，所以的最小值为8，故C正确;
对于D，令，，则，所以，
当且仅当，即，时等号成立，故D正确.
故选：
12.【答案】3
【解析】【分析】本题主要考查的是分数指数幂的运算，指对互化，属于基础题.
直接利用分数指数幂与指对互化求解即可.
13.【答案】或或或
【解析】【分析】
本题考查扇形面积，属于中档题，
根据扇形面积公式计算求解即可.
【解答】解：因为的面积为1，所以，解得，
当是锐角三角形时，扇形AOB的圆心角是或，
扇形的面积分别为或；
当是钝角三角形时，扇形AOB的圆心角是或，
扇形的面积分别为或；
故答案为或或或
14.【答案】
【解析】解：作出函数的图象如图所示，
令，则因为关于 x的方程有6个不同的实根，
所以方程在区间上有2个不同的实根，
设，
则，解得，
故实数a的取值范围是
15.【答案】解：因为，
所以等价于，且，
解得：或，所以集合或
所以
又因为等价于，
解得：，即，所以集合
当时，，
所以
因为“”是“”的充分不必要条件，所以集合是集合B的真子集，
所以，
解得故实数a的取值范围为

【解析】本题考查了集合的运算，以及充分必要条件的应用
16.【答案】解：因为角的终边过点，
所以，且，解得：，
所以，
因为，
所以
，
即
又因为角为第三象限角，所以，，
所以，即，
所以

【解析】本题主要考查任意角的三角函数的定义，同角三角函数基本关系式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于中档题．
利用任意角的三角函数的定义可求的值，进而得解；
由已知利用同角三角函数基本关系式，即可计算得解．
17.【答案】解：因为，，
所以，且，所以，
，
当时，
，
当或2时，所以
当时，，
当且仅当即时等号成立.
综上所述，当时，该水果树的单株利润最大，最大利润为645元.
【解析】详细解答和解析过程见【答案】
18.【答案】解：因为，则，，
因为函数在区间上有且仅有4个零点，
所以函数在区间上有且仅有4个零点，
结合余弦函数的图象与性质可得：，
解得：，
所以的取值范围为
当时，由可得：，所以，
因为不等式在上恒成立，
所以在上恒成立，又因为当时，，
所以，所以，
即，所以，故实数m的取值范围为
因为函数在区间内有两个不同的零点，所以在区间内有两个不同的零点，
即在区间内有两个不同的零点，
即函数与的图象在区间内有两个不同的交点，
由余弦函数的图象与性质可得：或，即或，
故实数t的取值范围为
【解析】本题考查了三角恒等变换，三角函数的性质，属于中档题．
利用换元法可得函数在区间上有且仅有4个零点，然后结合余弦函数的图象与性质即可得结果；
求出，问题转化为在上恒成立，进而求得结果；
问题转化为函数与的图象在区间内有两个不同的交点，可得t的不等式，计算可得结果.
19.【答案】解：因为函数是定义在R上的奇函数，所以，即①
又因为，所以，即②，
联立①②可得：，解得，代入①可得：
经检验，当，时，，满足题意.
由可得：，下面证明函数在R上为单调递增函数.
，，当时，，
因为，且为R上的增函数，所以，则，
所以，即，
所以函数在R上为单调递增函数;
因为当时，不等式恒成立，
所以当时，不等式恒成立，
由函数在R上为单调递增函数得：当时，，即恒成立，
令，，
则当即时，函数在上单调递增，
所以，所以即或，所以
当即时，函数在上单调递减，在上单调递增，所以，不符合题意;
当即时，函数在上单调递减，所以，所以，所以或，所以，
综上，实数t的取值范围为
【解析】本题考查函数的奇偶性和单调性的判断和运用，以及不等式恒成立问题解法，考查转化思想和运算能力、推理能力，属于较难题．
由定义在R上的奇函数，可得和，解得a与b，检验可得所求值；
由指数函数的单调性可判断的单调性；
由的奇偶性和单调性，可得当时，，即恒成立，可得所求范围．