





所属成套资源:冀教版(2024)数学七年级下册同步教学课件
数学七年级下册(2024)11.4 一元一次不等式的应用示范课课件ppt
展开
这是一份数学七年级下册(2024)11.4 一元一次不等式的应用示范课课件ppt,共29页。PPT课件主要包含了实际问题,1超过,2至少,3最多,12-x,解不等式,列不等式,结合实际确定答案,x≥125等内容,欢迎下载使用。
类比列一元一次方程解应用题的方法,能从实际问题中抽象出数量之间的不等关系,会解决有关一元一次不等式的简单问题,体会不等式在解决实际问题中的作用,发展应用意识和模型观念.
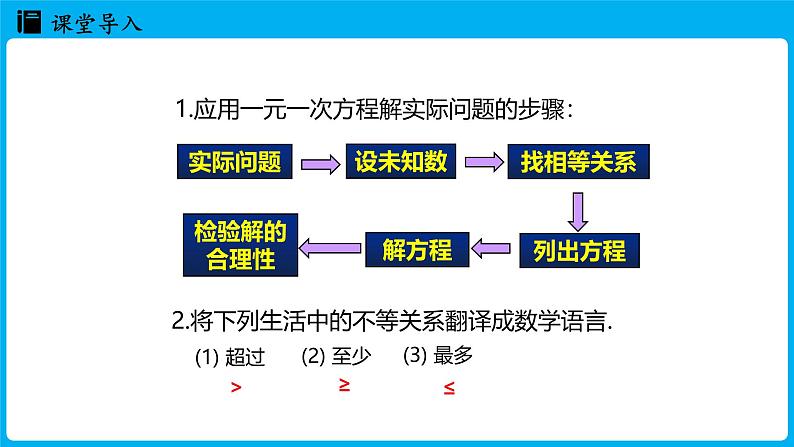
1.应用一元一次方程解实际问题的步骤:
2.将下列生活中的不等关系翻译成数学语言.
七年级(一)班的学生准备用500元购买甲、乙两种图书共12套,送给老区的幼儿园小朋友.已知甲种图书每套45元,乙种图书每套40元.那么这些钱最多能买甲种图书多少套?
问题1: 设可购买甲种图书x套,则购买甲种图书用钱为______元,购买乙种图书________套,购买乙种图书用钱为________元.
知识点 列一元一次不等式解决实际问题
问题2: 购买甲、乙两种图书所用钱数与500元有什么关系?
甲图书所用钱数 + 乙图书所用钱数 ≤ 500.
问题3: 你能用不等式把这种关系表示出来吗?
45x+40(12-x)≤ 500
问题4:解上面列出的不等式,并根据解集确定实际问题的答案.
解得x≤ 4,故最多购买甲图书4套.
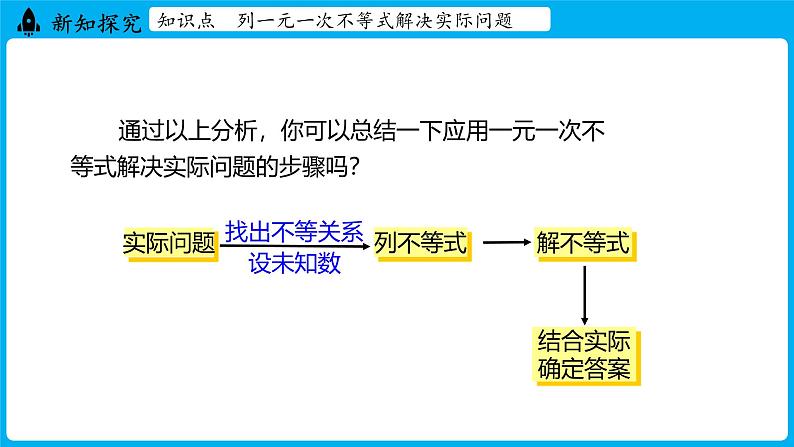
通过以上分析,你可以总结一下应用一元一次不等式解决实际问题的步骤吗?
例1 某商场为响应国家“绿色智能家电下乡”的惠农政策,决定采购一批智能家电,优惠销售给农民朋友. 商场从厂家直接购进甲、乙、丙三种不同的智能家电共80件,其中,甲种智能家电的件数是乙种智能家电件数的2倍,购买三种智能家电的总金额不超过13 200元,已知甲、乙、丙三种智能家电每件的出厂价格分别为120元,160元和200元. 那么该商场购进的乙种智能家电至少为多少件?
解析:题中的等量关系, 甲种智能家电的件数 + 乙种智能家电的件数 + 丙 种智能家电的件数 = 80 甲种智能家电的件数 = 2×乙种智能家电的件数 题中的不等关系, 120×甲种智能家电的件数+160×乙种智能家电的件数+200×丙种智能家电的件数≤13 200
根据题意列不等式,得 120×2x+160x+200(80-3x)≤13 200.
解这个不等式,得 x≥14.答:该商场购进的乙种智能家电至少为14件.
解:设购进乙种智能家电x件,则购进甲种智能家电2x件,购进丙种智能家电(80-3x)件.
归纳:生活中常用的不等关系与数学语言:超过 ,至少 ,最多 .
例2 某市青少年活动中心组织开展青少年乒乓球比赛,该比赛分小组循环赛和复赛两个阶段进行.在小组循环赛中,每人共有8场比赛,胜一场得3分,负一场得1分,积分超过16分可获得参加复赛的资格.如果要获得参加复赛的资格,那么参赛队员在小组循环赛中至少要胜多少场?
解析:题中的等量关系,胜的场数+负的场数=8题中的不等关系, 3×胜的场数+(-1)×负的场数≥16
解:设胜的场数为x,则负的场数为8-x. 根据题意列不等式,得 3x+(-1)×(8-x)≥16.
解这个不等式,得 x≥6. 答:参赛队员在小组循环赛中至少要胜6场.
解题通法:在用不等式解决实际问题时,当求出解集后,还要根据问题的实际意义确定问题的解.
练一练 当一个人坐下时,不宜提举超过4.5 kg的重物,以免受伤. 小明坐在书桌前,桌上有两本质量为1.2 kg的画册和一批每本质量为0.4 kg的记事本. 如果小明想坐着搬动这两本画册和一些记事本. 问他最多只应搬动多少本记事本?
解: 设小明应搬动x本记事本,则
解得 x≤5.25.
1.2×2+0.4x≤4.5.
答:小明最多只应搬动5本记事本.
因为x是整数,所以x 的最大值为5.
例3 三个连续正整数的和小于39,这样的正整数中,最大一组的和是多少?
解:设三个连续正整数分别为x﹣1,x,x+1. 根据题意列不等式,得 (x﹣1)+x+(x+1)<39.
解这个不等式,得 x<13. 所以当x=12时,三个连续正整数的和最大. 三个连续正整数的和为11+12+13=36.
例4 某商店购进一批水果,运输过程中质量损失10%,假设不计商店的其他费用.(1)如果商店在进价的基础上提高10%作为售价,则该商店的盈亏情况是_________;(填“盈”、“亏”或“不盈不亏”)
解析:利润=售价﹣进价. 设进价为a. 依题意,得利润 = (1﹣10%)×(1+10%)a﹣a=﹣0.01a.
(2)若该商店想要获得至少20%的利润,则这种水果的售价在原进价的基础上至少提高多少?
解:设水果的售价在原进价的基础上提高x. 据题意列不等式,得 (1﹣10%)(1+x) ≥ (1+20%). 解得 答:水果得售价在原进价的基础上至少提高 .
例5 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)(1)购买一件原价为450元的健身器材时,选择哪种活动更合算?
例5 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)(2)购买一件原价在500元以下的健身器材时,若选择活动一和选择活动二的付款金额相等,求一件这种健身器材的原价;
例5 某健身器材专卖店推出两种优惠活动,并规定购物时只能选择其中一种.活动一:所购商品按原价打八折;活动二:所购商品按原价每满300元减80元.(如:所购商品原价为300元,可减80元,需付款220元;所购商品原价为770元,可减160元,需付款610元)(3)购买一件原价在900元以下的健身器材时,原价在什么范围内,选择活动二比选择活动一更合算?设一件这种健身器材的原价为a元,请直接写出a的取值范围.
(3)当300≤a
相关课件
这是一份初中数学冀教版七年级下册第十章 一元一次不等式和一元一次不等式组10.4 一元一次不等式的应用课前预习ppt课件,共12页。PPT课件主要包含了一起探究,x≤4,x+2×3,不超过21元,x+2×3≤21,列出不等式,谁是聪明的消费者,设她还能买x支笔,笔记本,你能行等内容,欢迎下载使用。
这是一份冀教版七年级下册10.4 一元一次不等式的应用优质课ppt课件,文件包含河北教育版数学七年级下·104一元一次不等式的应用教学课件pptx、104一元一次不等式的应用教案docx、104一元一次不等式的应用同步练习docx等3份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
这是一份数学七年级下册10.4 一元一次不等式的应用习题ppt课件,共49页。PPT课件主要包含了答案呈现等内容,欢迎下载使用。









