高考十年真题数学分项汇编——集合与常用逻辑用语（含答案）

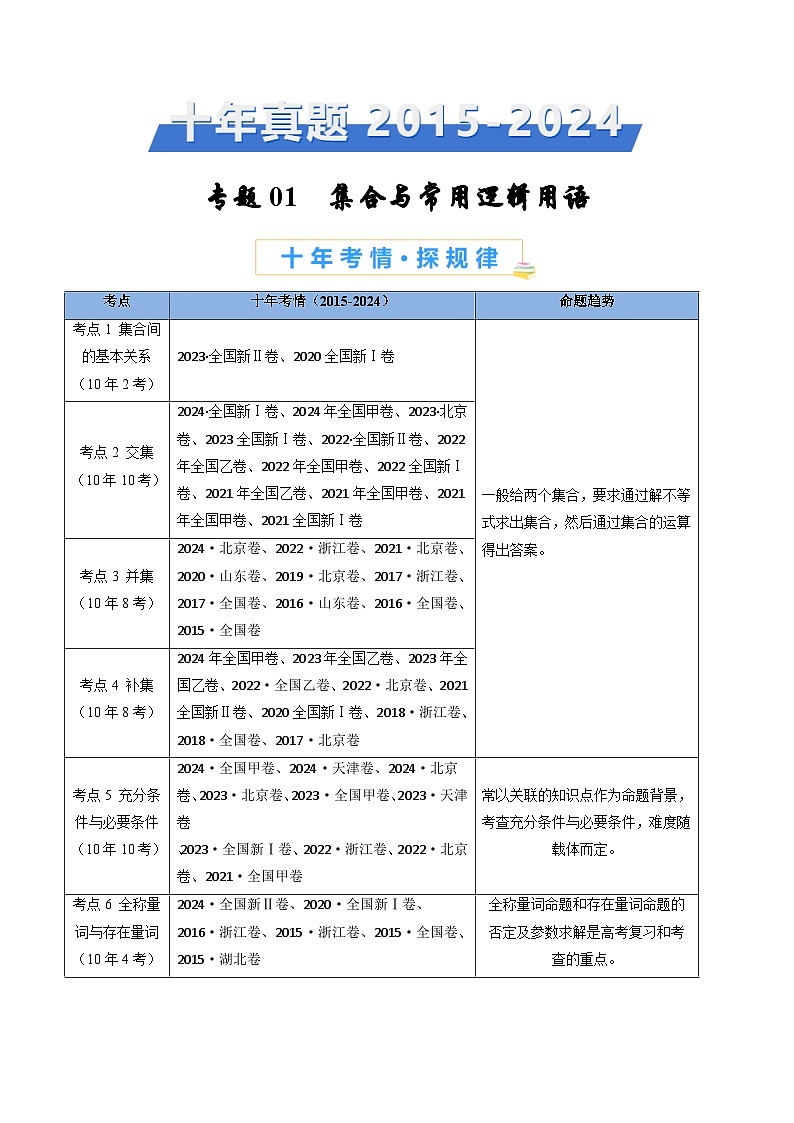
这是一份高考十年真题数学分项汇编——集合与常用逻辑用语（含答案），共17页。

考点01 集合间的基本关系
1．（2023·全国新Ⅱ卷·高考真题）设集合，，若，则（ ）．
A．2B．1C．D．
【答案】B
【分析】根据包含关系分和两种情况讨论，运算求解即可.
【详解】因为，则有：
若，解得，此时，，不符合题意；
若，解得，此时，，符合题意；
综上所述：.
故选：B.
2．（2020全国新Ⅰ卷·高考真题）已知，若集合，，则“”是“”的（ ）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
【答案】A
【分析】根据充分条件和必要条件的定义即可求解.
【详解】当时，集合，，可得，满足充分性，
若，则或，不满足必要性，
所以“”是“”的充分不必要条件，
故选：A.
考点02 交集
1．（2024·全国新Ⅰ卷高考真题）已知集合，则（ ）
A．B．C．D．
【答案】A
【分析】化简集合，由交集的概念即可得解.
【详解】因为，且注意到，
从而.
故选：A.
2．（2024年全国甲卷高考真题）若集合，，则（ ）
A．B．C．D．
【答案】C
【分析】根据集合的定义先算出具体含有的元素，然后根据交集的定义计算.
【详解】依题意得，对于集合中的元素，满足，
则可能的取值为，即，
于是.
故选：C
3．（2023·北京·高考真题）已知集合，则（ ）
A．B．
C．D．
【答案】A
【分析】先化简集合，然后根据交集的定义计算.
【详解】由题意，，，
根据交集的运算可知，.
故选：A
4．（2023全国新Ⅰ卷高考真题）已知集合，，则（ ）
A．B．C．D．
【答案】C
【分析】方法一：由一元二次不等式的解法求出集合，即可根据交集的运算解出．
方法二：将集合中的元素逐个代入不等式验证，即可解出．
【详解】方法一：因为，而，
所以．
故选：C．
方法二：因为，将代入不等式，只有使不等式成立，所以．
故选：C．
5．（2022·全国新Ⅱ卷高考真题）已知集合，则（ ）
A．B．C．D．
【答案】B
【分析】方法一：求出集合后可求.
【详解】[方法一]：直接法
因为，故，故选：B.
[方法二]：【最优解】代入排除法
代入集合，可得，不满足，排除A、D；
代入集合，可得，不满足，排除C.
故选：B.
【整体点评】方法一：直接解不等式，利用交集运算求出，是通性通法；
方法二：根据选择题特征，利用特殊值代入验证，是该题的最优解．
6．（2022年全国乙卷·高考真题）集合，则（ ）
A．B．C．D．
【答案】A
【分析】根据集合的交集运算即可解出．
【详解】因为，，所以．
故选：A.
7．（2022年全国甲卷·高考真题）设集合，则（ ）
A．B．C．D．
【答案】A
【分析】根据集合的交集运算即可解出．
【详解】因为，，所以．
故选：A.
8．（2022全国新Ⅰ卷·高考真题）若集合，则（ ）
A．B．C．D．
【答案】D
【分析】求出集合后可求.
【详解】，故，
故选：D
9．（2021年全国乙卷·高考真题）已知集合，，则（ ）
A．B．C．D．
【答案】C
【分析】分析可得，由此可得出结论.
【详解】任取，则，其中，所以，，故，
因此，.
故选：C.
10．（2021年全国甲卷·高考真题）设集合，则（ ）
A．B．C．D．
【答案】B
【分析】求出集合后可求.
【详解】，故，
故选：B.
11．（2021年全国甲卷·高考真题）设集合，则（ ）
A．B．
C．D．
【答案】B
【分析】根据交集定义运算即可
【详解】因为，所以,
故选：B.
【点睛】本题考查集合的运算，属基础题，在高考中要求不高，掌握集合的交并补的基本概念即可求解.
12．（2021全国新Ⅰ卷·高考真题）设集合，，则（ ）
A．B．C．D．
【答案】B
【分析】利用交集的定义可求.
【详解】由题设有，
故选：B .
考点03 并集
1．（2024·北京·高考真题）已知集合，，则（ ）
A．B．
C．D．
【答案】C
【分析】直接根据并集含义即可得到答案.
【详解】由题意得.
故选：C.
2．（2022·浙江·高考真题）设集合，则（ ）
A．B．C．D．
【答案】D
【分析】利用并集的定义可得正确的选项.
【详解】，
故选：D.
3．（2021·北京·高考真题）已知集合，，则（ ）
A．B．
C．D．
【答案】B
【分析】结合题意利用并集的定义计算即可.
【详解】由题意可得：.
故选：B.
4．（2020·山东·高考真题）设集合A={x|1≤x≤3}，B={x|2