2024-2025学年四川省德阳市高二上册第一次月考数学检测试题

这是一份2024-2025学年四川省德阳市高二上册第一次月考数学检测试题，共5页。试卷主要包含了请将答案正确填写在答题卡上， 已知一组数据等内容，欢迎下载使用。
注意事项：
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第Ⅰ卷（选择题）
一、单选题
1. 已知集合，，则（ ）
A. B.
C. D.
2. 在复平面内对应的点位于（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
3. 某实验中学共有职工150人，其中高级职称的职工15人，中级职称的职工45人，一般职员90人，现采用分层抽样抽取容量为30的样本，则抽取的高级职称、中级职称、一般职员的人数分别为（ ）
A. 5、10、15B. 3、9、18C. 3、10、17D. 5、9、16
4. 已知一组数据：4，6，7，9，11，13，则这组数据的第50百分位数为（ ）
A. 6B. 7C. 8D. 9
5. 从1，2，3，4，5中任取2个不同的数，取到的2个数之和为偶数的概率为（ ）
A. B. C. D.
6. 已知空间中非零向量，，且，，，则的值为（ ）
A. B. C. D.
7. 已知空间向量，空间向量满足且，则＝（ ）
A. B.
C. D.
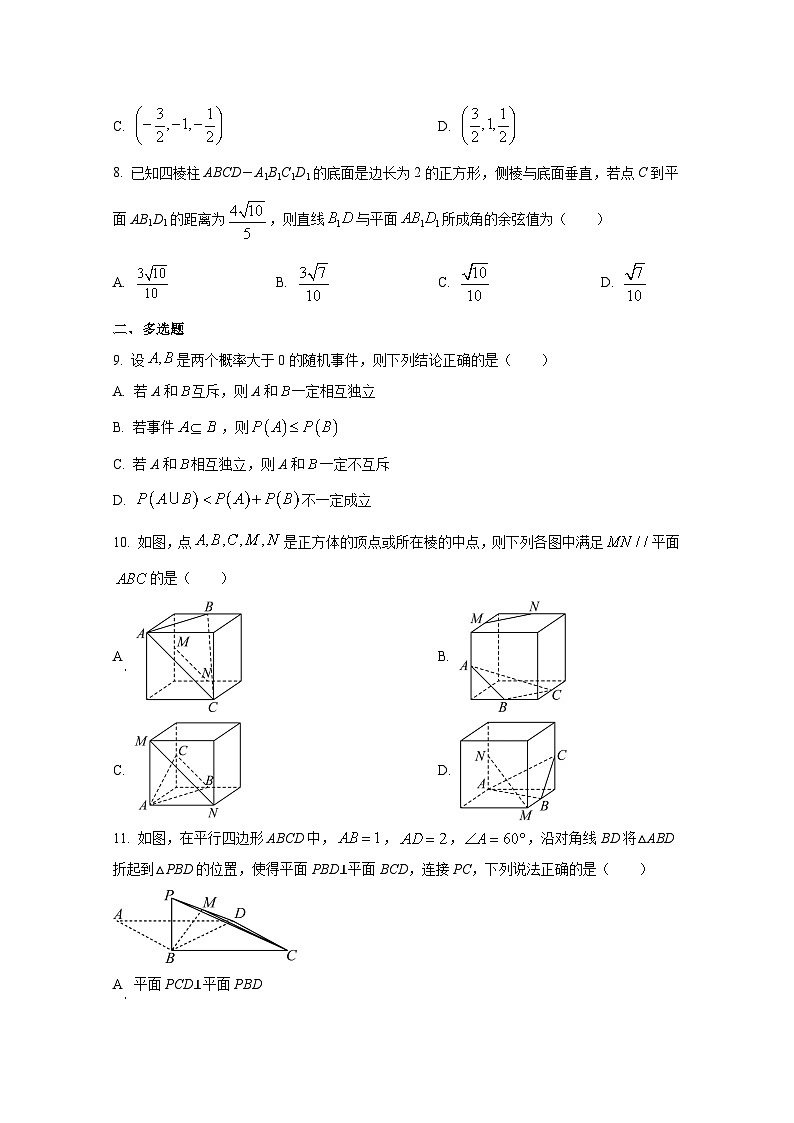
8. 已知四棱柱ABCD－A1B1C1D1的底面是边长为2的正方形，侧棱与底面垂直，若点C到平面AB1D1的距离为，则直线与平面所成角的余弦值为（ ）
A. B. C. D.
二、多选题
9. 设是两个概率大于0的随机事件，则下列结论正确的是（ ）
A. 若A和互斥，则A和一定相互独立
B. 若事件，则
C. 若A和相互独立，则A和一定不互斥
D. 不一定成立
10. 如图，点是正方体的顶点或所在棱的中点，则下列各图中满足平面的是（ ）
A B.
C. D.
11. 如图，在平行四边形ABCD中，，，，沿对角线BD将△ABD折起到△PBD的位置，使得平面PBD⊥平面BCD，连接PC，下列说法正确的是（ ）
A 平面PCD⊥平面PBD
B. 三棱锥外接球的表面积为
C. PD与平面PBC所成角的正弦值为
D. 若点M在线段PD上（包含端点），则△BCM面积的最小值为
第Ⅱ卷（选择题）
三、填空题
12. 如果从甲口袋中摸出一个红球的概率是，从乙口袋中摸出一个红球的概率是，现分别从甲乙口袋中各摸出1个球，则2个球都是红球的概率是________．
13. 已知正方体棱长为，点是的中点，则点A到直线的距离是__________．
14. 如图，在四棱锥中，平面，底面为正方形，，点分别为的中点，点为内的一个动点（包括边界），若平面，则点的轨迹的长度为__________.
四、解答题
15. 《中华人民共和国民法典》于2021年1月1日正式施行．某社区为了解居民对民法典的认识程度，随机抽取了一定数量的居民进行问卷测试（），并根据测试成绩绘制了如图所示的频率分布直方图.
（1）估计该组测试成绩的平均数和第57百分位数；
（2）该社区在参加问卷且测试成绩位于区间和的居民中，采用分层随机抽样，确定了5人.若从这5人中随机抽取2人作为该社区民法典宣讲员，设事件“两人的测试成绩分别位于和”，求.
16. 在直三棱柱ABC­A1B1C1中，∠ABC＝90°，BC＝2，CC1＝4，点E在线段BB1上，且EB1＝1，D，F，G分别为CC1，C1B1，C1A1的中点．

（1）证明：B1D⊥平面ABD；
（2）证明：平面EGF∥平面ABD.
17. 已知甲射击的命中率为0.8，乙射击的命中率为0.9，甲乙两人的射击相互独立．
（1）甲乙两人同时命中目标的概率；
（2）甲乙两人中至少有1人命中目标的概率．
18. 如图，圆柱的轴截面ABCD是正方形，点在底面圆周上，为垂足.
（1）求证.
（2）当直线与平面所成角的正切值为2时，
①求平面与平面夹角的余弦值；
②求点到平面距离.
19. 图1是直角梯形，，，四边形是边长为4的菱形，并且，以为折痕将折起，使点到达的位置，且，如图2.

（1）求证：平面平面；
（2）在棱上是否存在点，使得到平面的距离为，若存在，则的值；
（3）在（2）前提下，求出直线与平面所成角的正弦