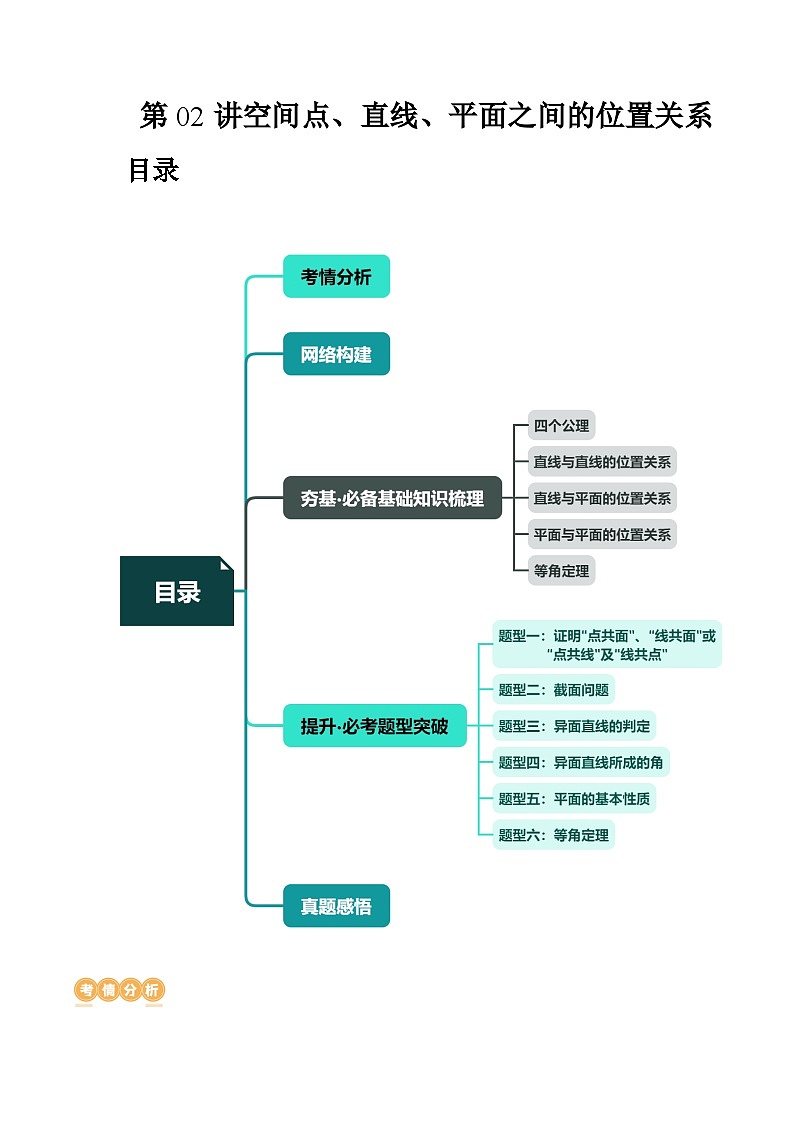
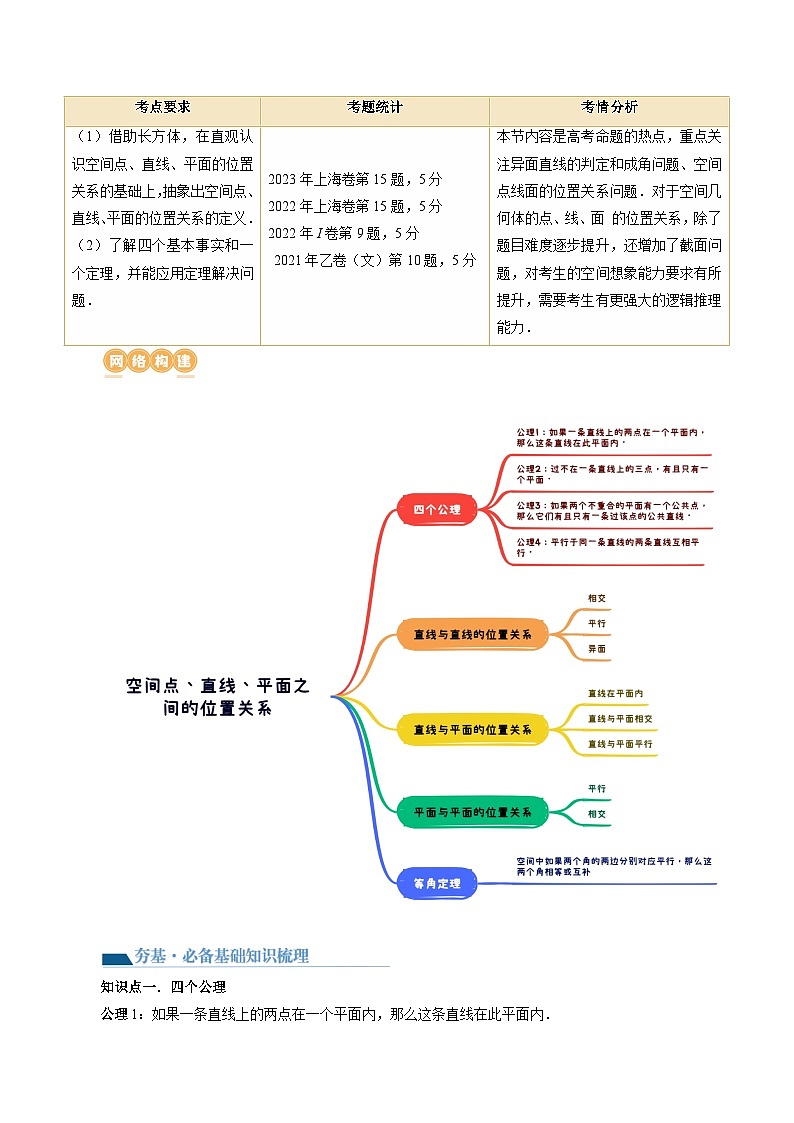
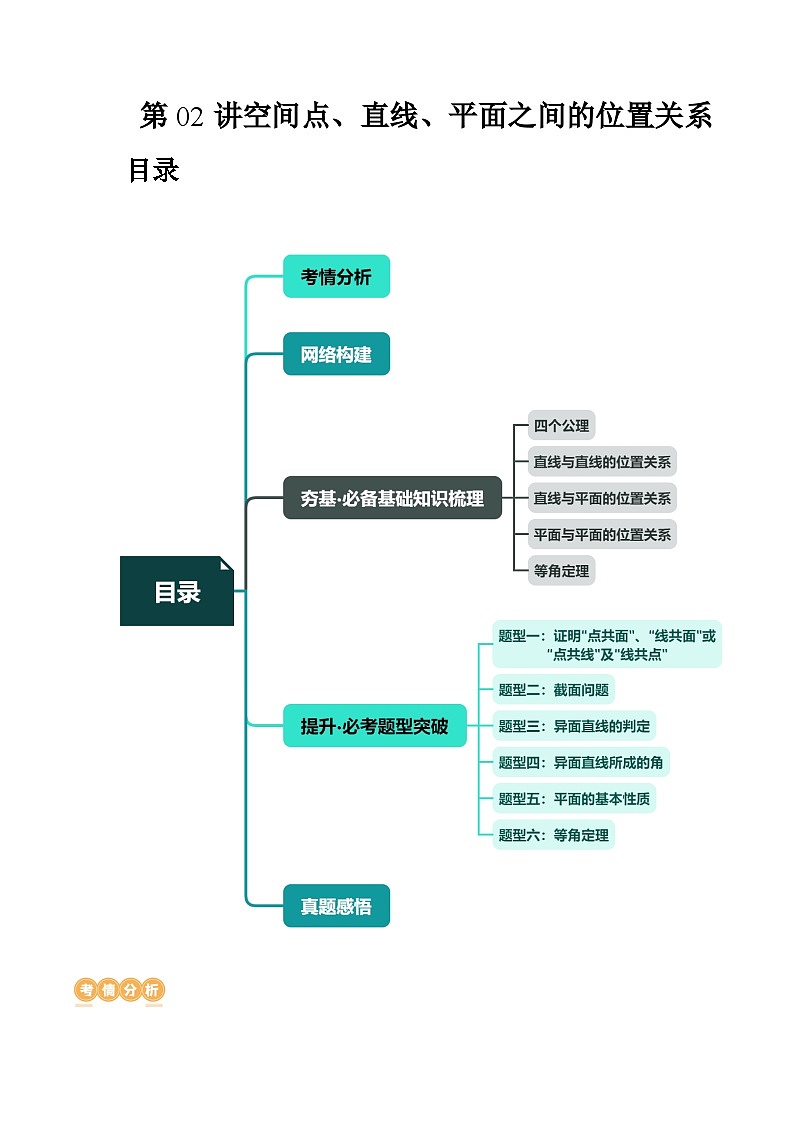
新高考数学一轮复习讲练测第02讲 空间点、直线、平面之间的位置关系（六大题型）（讲义）（2份，原卷版+解析版）

这是一份新高考数学一轮复习讲练测第02讲 空间点、直线、平面之间的位置关系（六大题型）（讲义）（2份，原卷版+解析版），文件包含新高考数学一轮复习讲练测第02讲空间点直线平面之间的位置关系六大题型讲义原卷版doc、新高考数学一轮复习讲练测第02讲空间点直线平面之间的位置关系六大题型讲义解析版doc等2份试卷配套教学资源，其中试卷共60页， 欢迎下载使用。

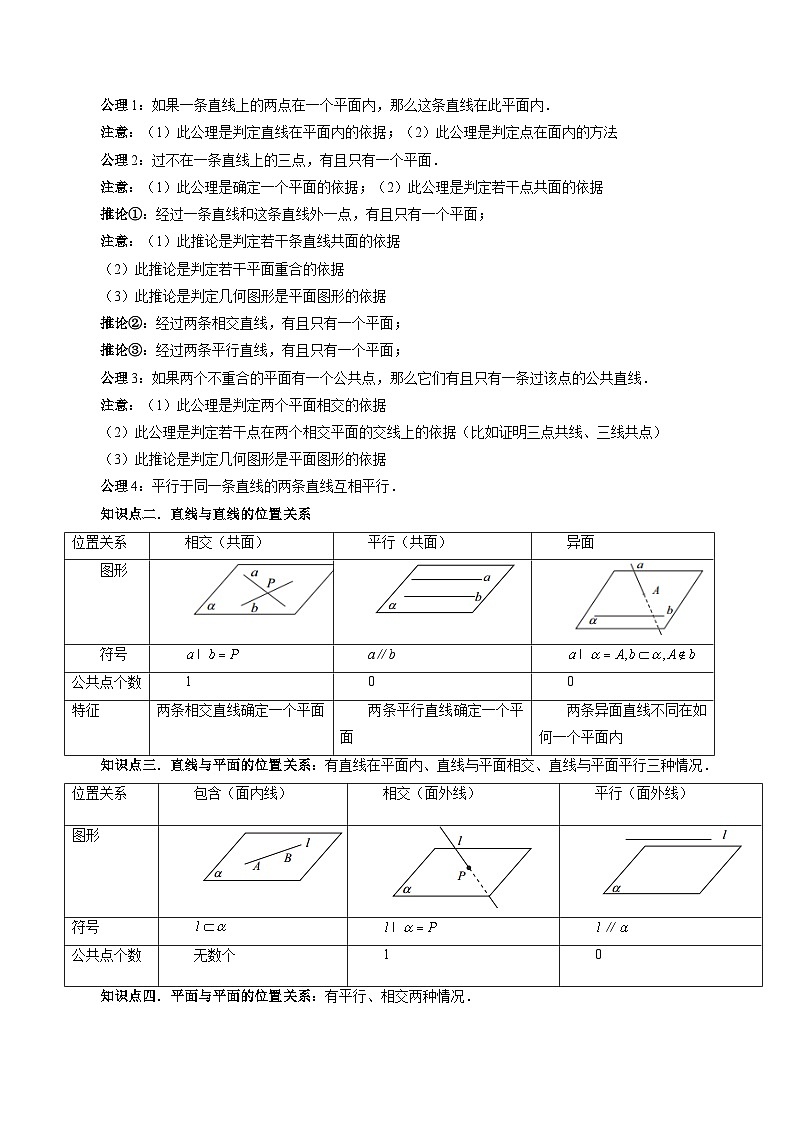
知识点一．四个公理
公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内．
注意：（1）此公理是判定直线在平面内的依据；（2）此公理是判定点在面内的方法
公理2：过不在一条直线上的三点，有且只有一个平面．
注意：（1）此公理是确定一个平面的依据；（2）此公理是判定若干点共面的依据
推论①：经过一条直线和这条直线外一点，有且只有一个平面；
注意：（1）此推论是判定若干条直线共面的依据
（2）此推论是判定若干平面重合的依据
（3）此推论是判定几何图形是平面图形的依据
推论②：经过两条相交直线，有且只有一个平面；
推论③：经过两条平行直线，有且只有一个平面；
公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．
注意：（1）此公理是判定两个平面相交的依据
（2）此公理是判定若干点在两个相交平面的交线上的依据（比如证明三点共线、三线共点）
（3）此推论是判定几何图形是平面图形的依据
公理4：平行于同一条直线的两条直线互相平行．
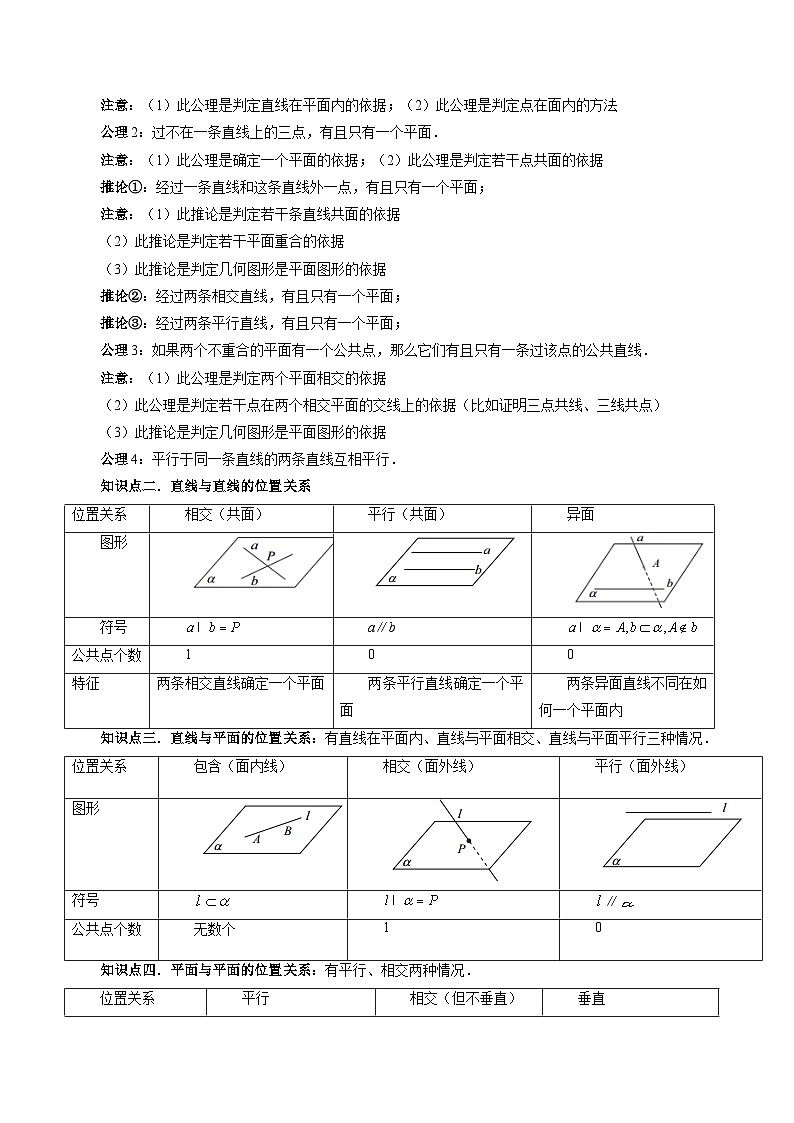
知识点二．直线与直线的位置关系
知识点三．直线与平面的位置关系：有直线在平面内、直线与平面相交、直线与平面平行三种情况．
知识点四．平面与平面的位置关系：有平行、相交两种情况．
知识点五．等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．
题型一：证明“点共面”、“线共面”或“点共线”及“线共点”
例1．（2023·山西大同·高一校考期中）如图所示，在空间四边形中，，分别为，的中点，，分别在，上，且，求证：

(1)，，，四点共面；
(2)与的交点在直线上．
【解析】（1）：：：，，
，分别为，的中点，，，
，，，四点共面．
（2）、不是、的中点，
，且，
与必相交，设交点为，
平面，平面，
平面，且平面，
平面平面，，
与的交点在直线上．
例2．（2023·陕西西安·高一校考期中）（1）已知直线，直线与，都相交，求证：过，，有且只有一个平面；
（2）如图，在空间四边形中，，分别是，的中点，，分别是边，上的点，且.求证：直线，，相交于一点.

【解析】（1）证明：设直线与，分别交于点，
如图1，

因为，所以确定一个平面，记为平面，
因为点直线，点直线，所以，，
所以直线，即平面，所以过，，有且只有一个平面；
（2）在空间四边形中，连接，
因为分别为的中点，则，且，
又由，则，且，
故，且，故四边形为梯形，与交于一点，
设与交于点，如图2，

由于平面，点在平面内，同理点在平面内，
又因为平面平面，
所以点在直线上，
故直线相交于一点.
例3．（2023·河南信阳·高一校联考期中）如图，在正方体中，E，F分别是上的点，且.

(1)证明：四点共面；
(2)设，证明：A，O，D三点共线.
【解析】（1）证明：如图，连接.

在正方体中，，所以，
又，且，
所以四边形是平行四边形，所以，
，所以四点共面；
（2）证明：由，，又平面，平面，
同理平面ABCD，又平面平面，
，即A，O，D三点共线.
变式1．（2023·全国·高一专题练习）如图所示，在空间四边形ABCD中，E，F分别为AB，AD的中点，G，H分别在BC，CD上，且.求证：
(1)E､F､G､H四点共面；
(2)EG与HF的交点在直线AC上.
【解析】（1）∵，∴.
∵E，F分别为AB，AD的中点，∴，且，
∴，∴E，F，G，H四点共面.
（2）∵G，H不是BC，CD的中点，∴，∴，
由（1）知，故EFHG为梯形.
∴EG与FH必相交，设交点为M，
∴平面ABC，平面ACD，
∴平面ABC，且平面ACD，
∴，即GE与HF的交点在直线AC上.
变式2．（2023·云南楚雄·高一统考期中）如图，在正四棱台中，E，F，G，H分别为棱，，AB，BC的中点．

(1)证明E，F，G，H四点共面；
(2)证明GE，FH，相交于一点．
【解析】（1）证明：连接AC，，如图所示，

因为为正四棱台，所以，
又E，F，G，H分别为棱，，AB，BC的中点，所以，，
则，所以E，F，G，H四点共面．
（2）因为，所以，所以EFHG为梯形，则EG与FH必相交．
设，因为平面，所以平面，
因为平面，所以平面，
又平面平面，所以，
则GE，FH，交于一点．
变式3．（2023·全国·高三专题练习）如图所示，在正方体中，E，F分别是的中点．
(1)求证：三线交于点P；
(2)在（1）的结论中，G是上一点，若FG交平面ABCD于点H，求证：P，E，H三点共线．
【解析】（1）证明：连接，，
正方体中，E，F分别是的中点，
∴且，
∵且，
∴且，
∴EC与相交，设交点为P，
∵PEC，EC平面ABCD，∴P平面ABCD；
又∵，平面，∴平面，
∴P为两平面的公共点，
∵平面平面，∴，
∴三线交于点P；
（2）
在（1）的结论中，G是上一点，FG交平面ABCD于点H，
则FH平面，∴平面，又平面ABCD，
∴平面平面ABCD，
同理，平面平面ABCD，
平面平面ABCD，
∴P，E，H都在平面与平面ABCD的交线上，
∴P，E，H三点共线．
【解题方法总结】
共面、共线、共点问题的证明
（1）证明共面的方法：先确定一个平面，然后再证其余的线（或点）在这个平面内．
（2）证明共线的方法：先由两点确定一条直线，再证其他各点都在这条直线上．
（3）证明共点的方法：先证其中两条直线交于一点，再证其他直线经过该点．
题型二：截面问题
例4．（2023·全国·高三对口高考）如图，正方体的棱长为，动点P在对角线上，过点P作垂直于的平面，记这样得到的截面多边形（含三角形）的周长为y，设，则当时，函数的值域为（ ）

A．B．C．D．
【答案】A
【解析】

如图，连接， ，平面，平面，则，
又，，平面，平面，
所以平面，又平面，所以，
同理，，平面，平面，所以平面，
因此平面与平面重合或平行，
取的中点，连接，则，，
同理可证平面，由于，，所以三棱锥是正三棱锥，
与平面的交点是的中心，
正方体棱长为，则，，
所以，所以，
由棱锥的平行于底面的截面的性质知，当平面从平面平移到平面时，，即，
，，显然，


平面过平面再平移至平面时，如图，把正方形沿旋转到与正方形在同一平面内，
如图，则共线，由正方形性质得，同理，，
因此此种情形下，截面的周长与截面的周长相等，平移平面，一直到平面位置处，
由正方体的对称性，接着平移时，截面周长逐渐减少到，
综上，的值域是．
故选：A.
例5．（2023·北京东城·高三北京市第十一中学校考阶段练习）如图，正方体的棱长为1，E，F，G分别为线段上的动点（不含端点），

①异面直线与AF所成角可以为
②当G为中点时，存在点E，F使直线与平面AEF平行
③当E，F为中点时，平面AEF截正方体所得的截面面积为
④存在点G，使点C与点G到平面AEF的距离相等
则上述结论正确的是（ ）
A．①③B．②④C．②③D．①④
【答案】C
【解析】对①：因为//，故与的夹角即为与的夹角，
又当与重合时，取得最大值，为；
当与点重合时，取得最小值，设其为，则，故；
又点不能与重合，故，故①错误；
对②：当为中点时，存在分别为的中点，满足//面，证明如下：
取的中点为，连接，如下所示：

显然//，又面面，故//面；
又易得//，面面，故//面；
又面，故面//面，
又面，故//面，故②正确；
对③：连接，如下所示：

因为////，故面即为平面截正方体所得截面；
又，故该截面为等腰梯形，又，，
故截面面积，故③正确；
对④：连接，取其中点为，如下所示：

要使得点到平面的距离等于点到平面的距离，只需经过的中点，
显然当点分别为所在棱的中点时，不存在这样的点满足要求，故④错误.
故选：C.
例6．（2023·河南·模拟预测）在正方体中，M，N分别为AD，的中点，过M，N，三点的平面截正方体所得的截面形状为（ ）
A．六边形B．五边形C．四边形D．三角形
【答案】B
【解析】
在上取点，且，取中点为，连接.
在上取点，且，连结.
因为，，
所以，所以.
又，所以，所以，
所以，.
因为分别为的中点，所以，且.
根据正方体的性质，可知，且，
所以，，且，
所以，四边形是平行四边形，
所以，，所以.
同理可得，.
所以，五边形即为所求正方体的截面.
故选：B.
变式4．（2023·河南·模拟预测）在正方体中，分别为，的中点，则下列结论正确的个数为（ ）
①平面 ；②；③直线与所成角的余弦值为
④过三点的平面截正方体所得的截面为梯形
A．1B．2C．3D．4
【答案】B
【解析】连接，交于点，则是的中点，连接，由于是中点，可得，
所以四边形是平行四边形，所以,
又平面，平面，所以平面，即①正确；
连接，则，在正方体中，平面，又平面，所以,
又，平面，平面，所以平面，若，则平面或平面，而与平面相交，所以与不垂直，即②错误；
由于，所以为直线与所成角（或补角），
设正方体棱长为2，
则,所以由余弦定理得，即③正确；
因为平面与平面平行，则过三点的截面与这两个平面的交线平行，由于其中一条交线是,另一交线过点，所以在平面内作与平行（是靠近的四等分点），连接，同理作出与平行（是靠近的三等分点），从而得到截面，可知截面是五边形，即④错误；
综上，正确的个数是2个.
故选：B.
变式5．（2023·上海闵行·高三上海市七宝中学校考阶段练习）在棱长为2的正方体中，E，F分别为AB，BC的中点，对于如下命题：①异面直线与所成角的余弦值为；②点P为正方形内一点，当平面时，DP的最小值为；③过点，E，F的平面截正方体所得的截面周长为；④当三棱锥的所有顶点都在球O的表面上时，球O的体积为．则正确的命题个数为（ ）
A．1B．2C．3D．4
【答案】C
【解析】对于①，，
在中即为异面直线与所成的角，
，
异面直线与所成的角的余弦值为．故①错误；
对于②，取的中点的中点，取的中点，连接，，，
，
同理可得，
又面，面，面，面，
面，面，
又，面，
面面，
又面，面，
轨迹为线段，
在中，过作，此时取得最小值，
在中，，，，
在中，，，，
在中，，，，
如图，在中，．故②正确；
对于③，过点的平面截正方体，
平面平面，则过点的平面必与、各交于一点，
设过点的平面必与与分别交于、，
过点的平面与平面和平面分别交于与，，同理可得，
如图过点的平面截正方体所得的截面图形为五边形，
如图以为原点，分别以方向为轴､轴､轴正方向建立空间直角坐标系，
设，，
则，，，，，
，，，，
，，
，解得，
，，
，，
在中，，，，同理：，
在中，，，，同理：
在中，，，
，
即过点的平面截正方体所得的截面周长为．故③正确；
对于④，如图所示，取的中点，则，过作，
且使得，则为三棱锥的外接球的球心，
所以为外接球的半径，
在中，，
，则，
．故④正确，
故选：C．
变式6．（2023·河南新乡·统考三模）如图，在棱长为2的正方体中，是棱的中点，过三点的截面把正方体分成两部分，则这两部分中大的体积与小的体积的比值为（ ）
A．B．C．D．
【答案】A
【解析】连接，设平面与平面交于，
因为平面平面，平面与平面交于，
则，又，
则，又是棱的中点，则F是BC的中点.
，,
，
，故.
故选：A.
变式7．（2023·新疆·校联考二模）已知在直三棱柱中，E，F分别为，的中点，，，，，如图所示，若过A、E、F三点的平面作该直三棱柱的截面，则所得截面的面积为（ ）
A．B．C．D．
【答案】B
【解析】解析：延长，且与相交于，连接EG，并与相交于，连接FD，则四边形AEDF为所求的截面.
在中，由，，得.
在中，由，，得.
因为为的中点，所以由平面几何知识可知，.
所以，，即为AG的中点，所以.
又由，可得，
又，，所以.
在中，由，，得，所以.
所以在中，有，，，
即，所以.又注意到，
，
则四边形AEDF的面积为.
故选：B．
变式8．（2023·新疆阿克苏·校考一模）已知，，是正方体的棱，，的中点，则平面截正方体所得的截面是（ ）
A．三角形B．四边形C．五边形D．六边形
【答案】D
【解析】如图所示，分别取，，的中点，，，连接 ，，，，，，则，.
，.
同理可得，.
由基本事实及其三个推论得，，，，，六点共面，
所以平面截正方体所得的截面是六边形.
故选：D.
变式9．（2023·重庆沙坪坝·高三重庆一中校考期中）在棱长为3的正方体中，点Р是侧面上的点，且点Р到棱与到棱AD的距离均为1，用过点Р且与垂直的平面去截该正方体，则截面在正方体底面ABCD的投影多边形的面积是（ ）
A．B．5C．D．8
【答案】C
【解析】
由题意可以作出与垂直的平面，
利用面面平行可作出过点P且平行于平面的平面GJKLNM，
则平面GJKLNM与垂直，
作出点M，N的投影O，Q，
平面AOQCKJ的面积S即为所求，
已知正方体棱长为3，点Р到棱与到棱AD的距离均为1，
所以点G，J，K，L，N，M均为各棱的三等分点
，
故选：C.
【解题方法总结】
（1）作截面应遵循的三个原则：①在同一平面上的两点可引直线；②凡是相交的直线都要画出它们的交点；③凡是相交的平面都要画出它们的交线．
（2）作交线的方法有如下两种：①利用基本事实3作交线；
②利用线面平行及面面平行的性质定理去寻找线面平行及面面平行，然后根据性质作出交线．
题型三：异面直线的判定
例7．（2023·全国·高三对口高考）两条直线分别和异面直线都相交，则直线的位置关系是（ ）
A．一定是异面直线B．一定是相交直线
C．可能是平行直线D．可能是异面直线，也可能是相交直线
【答案】D
【解析】已知直线与是异面直线，直线与直线分别与两条直线与直线相交于点，

根据题意可得当点与点重合时，两条直线相交，当点与点不重合时，两条直线异面，
所以直线的位置关系是异面或相交.
故选:D．
例8．（2023·全国·高三专题练习）如图，已知正方体，点在直线上，为线段的中点，则下列命题中假命题为（ ）
A．存在点，使得
B．存在点，使得
C．直线始终与直线异面
D．直线始终与直线异面
【答案】C
【解析】正方体中，易得平面，因为点在直线上，为线段的中点，
当点和点重合时，平面，，故A正确；
连接、，当点为线段的中点时，为三角形的中位线，即，故B正确；
平面，当点和点重合时，平面，所以直线和在同一平面内，故C错误；
平面，平面，，所以直线始终与直线不相交，且不平行，
所以直线与直线是异面直线，故D正确；
故选：C
例9．（2023·四川绵阳·高三绵阳南山中学实验学校校考阶段练习）在底面半径为1的圆柱中，过旋转轴作圆柱的轴截面ABCD，其中母线AB=2，E是弧BC的中点，F是AB的中点，则（ ）
A．AE=CF，AC与EF是共面直线
B．，AC与EF是共面直线
C．AE=CF，AC与EF是异面直线
D．，AC与EF是异面直线
【答案】D
【解析】如图，在底面半径为1的圆柱中，母线，，是的中点，则，
因为是的中点，又，则，
，，
，
在中，是的中点，是的中点，，
与是共面直线，
若AC与EF是共面直线，则在同一平面，显然矛盾，故AC与EF是异面直线
故选：D．
变式10．（2023·上海浦东新·高三华师大二附中校考阶段练习）已知正方体中，，，分别是棱，，的中点，是线段上的动点，则下列直线中，始终与直线异面的是（ ）
A．B．C．D．
【答案】A
【解析】对于选项A，面，面，面，所以直线与异面；
对于选项B，当与重合时，因为，又，，分别是棱，，的中点，所以，所以，选项B错误；
对于选项C，连接，在正方体中，易得且，所以与相交，即当与重合时，与相交，选项C错误；
对于选项D，取中点，连交于，连，因为且，所以且，故当与重合时，与相交，选项D错误.
故选：A.
变式11．（2023·上海·高三校联考阶段练习）如图所示，正三棱柱的所有棱长均为1，点P、M、N分别为棱、AB、的中点，点Q为线段MN上的动点．当点Q由点N出发向点M运动的过程中，以下结论中正确的是（ ）
A．直线与直线CP可能相交B．直线与直线CP始终异面
C．直线与直线CP可能垂直D．直线与直线BP不可能垂直
【答案】B
【解析】在正三棱柱中，
因为点M、N分别为棱AB、的中点，所以，
又平面，平面，
所以平面，
因为平面，，，
所以四点不共面，
所以直线与直线CP始终异面，故A错误，B正确；
对于C，设，
则，
，
若直线与直线CP垂直，则，
即，
所以，
即，解得，
因为，所以不存在点使得直线与直线CP垂直，故C错误；
对于D，连接，
因为为的中点，所以，
又因平面，平面，
所以，
因为平面，
所以平面，
又平面，所以，
所以当点在的位置时，直线与直线BP垂直，故D错误.
故选：B.
变式12．（2023·吉林长春·高三长春市第六中学校考期末）如图，在底面为正方形的棱台中，、、、分别为棱，，，的中点，对空间任意两点、，若线段与线段、都不相交，则称点与点可视，下列选项中与点可视的为（ ）
A．B．C．D．
【答案】D
【解析】根据棱台的性质可知，连接、、、、，
因为、分别为棱，的中点，
所以，又底面为正方形，所以，所以，所以四边形为梯形，
所以与相交，与相交，故B、C错误；
因为，所以四边形是梯形，所以与相交，故A错误；
因为为梯形，为的中点，即，则、、、四点不共面，所以与不相交，
若与相交，则、、、四点共面，
显然、、、四点共面，平面，所以、、、四点不共面，即假设不成立，
所以与不相交，即点与点可视，故D正确．
故选：D．
【解题方法总结】
判定空间两条直线是异面直线的方法如下：
（1）直接法：平面外一点A与平面内一点B的连线和平面内不经过B点的直线是异面直线．
（2）间接法：平面两条不可能共面（平行，相交）从而得到两线异面．
题型四：异面直线所成的角
例10．（2023·全国·高三专题练习）如图,在正方体中,点E,F分别是棱AD,的中点,则异面直线与BF所成角的大小为 ．
【答案】
【解析】取中点为,连接,记与交点为,如图所示:
因为G,F分别是棱,的中点,
所以,且,故四边形为平行四边形,
所以,所以与BF所成角即为与所成角,
因为正方体,E,G是棱AD,的中点,
所以,
所以,即,
因为,所以,
所以,
故与所成角为,即与BF所成角为.
故答案为:
例11．（2023·高三课时练习）已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的大小为 ．
【答案】
【解析】解:由题知,取中点为，连接如图所示:
不妨设正四面体棱为6,
根据分别为中点得：，
因为与为等边三角形,
所以，故，同理，
在中,由余弦定理可得:
，
故,
因为,
所以异面直线CE与BD所成角，即直线CE与所成角，即,
故异面直线CE与BD所成角为.
故答案为:
例12．（2023·新疆喀什·高三统考期中）如图是一个正方体的平面展开图，在这个正方体中，下列说法中，正确的序号是 .
（1）直线与直线相交；
（2）直线与直线平行；
（3）直线与直线是异面直线；
（4）直线与直线成角.
【答案】（3）（4）/(4)(3)【解析】由正方体的平面展开图可得正方体，
可得与为异面直线，故（1）错误；
与为异面直线，故（2）错误；
直线与直线是异面直线，故（3）正确；
连接，，由正方体的性质可得，所以为异面直线与直线所成的角，因为为等边三角形，所以，即直线与直线所成角为，故（4）正确；
故答案为：（3）（4）．
变式13．（2023·全国·高三专题练习）如图，将正方体沿交于一顶点的三条棱的中点截去一小块，八个顶点共截去八小块，得到八个面为正三角形、六个面为正方形的“阿基米德多面体”，则异面直线与所成角的大小是
【答案】
【解析】如图所示，由题可知，四边形和均为正方形，为正三角形，
，，
或其补角为异面直线与所成角，
而为正三角形，
，
即异面直线与所成角的大小是.
故答案为：.
变式14．（2023·全国·高三对口高考）线段的两端分别在直二面角的两个面内，且与这两个面都成角，则直线与所成的角等于 ．
【答案】/
【解析】如图：

过分别作棱的垂线，垂足设为连结，
由直线垂直于平面的性质定理知，.
所以.
作且，则为直线与所成的角.
连结，可得，，所以，
所以三角形为直角三角形.
设，，所以，
所以.
直线与所成的角等于.
故答案为：.
变式15．（2023·全国·高三专题练习）如图，等腰梯形沿对角线翻折，得到空间四边形，若，则直线与所成角的大小可能为 .（写出一个值即可）
【答案】（答案在内即可）
【解析】由题意，补全等腰梯形为正三角形，则直线与所成角的大小为直线与所成角，易得当等腰梯形沿对角线翻折时，的轨迹为以为顶点，为高的圆锥侧面，设，在上取使得，则直线与所成角即，故，因为，，故，故，故只需写出内的角度即可，如

故答案为：（答案在内即可）
【解题方法总结】
（1）点、直线、平面位置关系的判定，注意构造几何体（长方体、正方体）模型来判断，常借助正方体为模型．
（2）求异面直线所成的角的三个步骤
一作：根据定义作平行线，作出异面直线所成的角．
二证：证明作出的角是异面直线所成的角．
三求：解三角形，求出所作的角．
题型五：平面的基本性质
例13．（多选题）（2023·湖北荆门·荆门市龙泉中学校考模拟预测）已知，是两个不同的平面，则下列命题正确的是（ ）
A．若，且，则
B．若A，B，C是平面内不共线三点，，，则
C．若且，则直线
D．若直线，直线，则a与b为异面直线
【答案】ABC
【解析】对于A，由根据且，则是平面和平面的公共点，
又，由基本事实3（公理2）可得，故A正确；
对于B，由基本事实1（公理3）：过不在一条直线上的三个点，有且只有一个平面，
又，且，则，故B正确；
对于C，由基本事实2（公理1）：如果一条直线上的两个点在一个平面内，那么这条直线在这个平面内，故C正确；
对于D，由于平面和平面位置不确定，则直线与直线位置亦不确定，可能异面、相交、平行、重合，故D错误.
故选：ABC.
例14．（多选题）（2023·全国·高三专题练习）有下列命题：
①经过三点确定一个平面；
②梯形可以确定一个平面；
③两两相交的三条直线最多可以确定三个平面；
④如果两个平面有三个公共点，则这两个平面重合．
其中正确命题是（ ）
A．①B．②C．③D．④
【答案】BC
【解析】对于①，经过不共线的三点确定一个平面，故①不正确；
对于②，因为梯形的两底边平行，经过两条平行直线确定一个平面，故②正确；
对于③，当三条直线交于不同的三点时，三条直线只确定一个平面；当三条直线交于一点时，三条直线最多确定三个平面，故③正确；
对于④，当两个平面的三个公共点在一条直线上时，这两个平面相交于这条直线，不一定重合，故④不正确.
故选：BC
例15．（多选题）（2023·全国·高三专题练习）我们知道，平面几何中有些正确的结论在空间中不一定成立．下面给出的平面几何中的四个真命题， 在空间中仍然成立的有（ ）
A．平行于同一条直线的两条直线必平行
B．垂直于同一条直线的两条直线必平行
C．一个角的两边分别平行于另一个角的两边，那么这两个角相等或互补
D．一个角的两边分别垂直于另一个角的两边，那么这两个角相等或互补
【答案】AC
【解析】根据线线平行具有传递性可知A正确；
空间中垂直于同一条直线的两条直线，位置关系可能是异面、相交、平行，故B错误；
根据定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补可知C正确；
如图，且，
则但和的关系不确定，
故D错误.
故选：AC
变式16．（多选题）（2023·重庆沙坪坝·高三重庆市第七中学校校考阶段练习）下列命题中错误的是（ ）
A．空间三点可以确定一个平面
B．三角形一定是平面图形
C．若A，，，既在平面内，又在平面内，则平面和平面重合
D．四条边都相等的四边形是平面图形
【答案】ACD
【解析】对于A：若空间中三点共线，则无法确定平面，故A错误；
对于B：三角形一定是平面图形，故B正确；
对于C：若A，，，既在平面内，又在平面内，则此四点可能在平面与平面的交线上，无法确定平面和平面是否重合，故C错误；
对于D：四条边都相等的四边形可能是空间四边形，故D错误；
故选：ACD
变式17．（多选题）（2023·全国·模拟预测）如图，点，，，分别是正方体中棱，，，的中点，则（ ）
A．B．
C．直线，是异面直线D．直线，是相交直线
【答案】BD
【解析】如图，取棱的中点，的中点，连接，，，，，，，
在正方体中，∵，
∴，，，四点共面，同理可得，，，四点共面，，，，四点共面，
∴，，，，，六点共面，均在平面内，
∵，，
，，平面，
∴与是相交直线．由正方体的结构特征及中位线定理可得，
∴，即．
故选：BD．
变式18．（多选题）（2023·全国·高三专题练习）如图，正方体的棱长为1，线段上有两个动点E、F，且，则下列结论中正确的是（ ）
A．线段上存在点E、F使得B．平面ABCD
C．的面积与的面积相等D．三棱锥A-BEF的体积为定值
【答案】BD
【解析】如图所示，AB与为异面直线，故AE与BF也为异面直线，A错误；
，故平面ABCD，故B正确；
由图可知，点A和点B到EF的距离是不相等的，C错误；
连结BD交AC于O，则AO为三棱锥A-BEF的高，
，
三棱锥A-BEF的体积为为定值，D正确；
故选：BD.
题型六：等角定理
例16．（2023·河南新乡·新乡市第一中学校考模拟预测）在棱长均相等的四面体中，为棱不含端点上的动点，过点A的平面与平面平行若平面与平面，平面的交线分别为，，则，所成角的正弦值的最大值为 ．
【答案】/
【解析】连接,
由题意知过点A的平面与平面平行，平面与平面，平面的交线分别为，，
由于平面平面，平面平面，平面平面，
所以，，
所以或其补角即为，所成的平面角，
设正四棱锥的棱长为，，，则，
在中，
由余弦定理得，
同理求得，
故在中，，
，
由于，则，进而，
当时取等号，
故的最小值为，进而，
故的最大值为，
故答案为：．
例17．（2023·全国·高三专题练习）过正方体的顶点在空间作直线，使与平面和直线所成的角都等于，则这样的直线共有 条．
【答案】2
【解析】在正方体中，与平面垂直，再根据等角定理，问题可以转化为过点A与、都成的直线有几条．
考虑到，夹角为，所以同一平面的角平分线与，的夹角大小为，
因为，从而存在两条直线满足条件．而，的外角为120度，所以不存在外角平分线满足条件．
综上，满足条件的直线共2条．
故答案为：2.
例18．（2023·高三课时练习）若空间两个角与的两边对应平行，当时，则 ．
【答案】60°或120°
【解析】当空间两个角与的两边对应平行，且两边的方向完全一致时，；
当空间两个角与的两边对应平行，且两边方向不完全一致时，.
故答案为：60°或120°
变式19．（2023·全国·高三专题练习）设和的两边分别平行，若，则的大小为 .
【答案】45°或135°/135°或45°
【解析】根据等角定理：一个角的两边平行于另外一个角的两边，则这两个角相等或互补.
故答案为：45°或135°.
变式20．（2023·全国·高三专题练习）空间四边形的对角线互相垂直且相等，顺次连接这个四边形各边中点，所组成的四边形是 .
【答案】正方形
【解析】连接、，
、、、分别为各边的中点，
，，，，
，，
四边形是平行四边形，
，且，
，且，
四边形是正方形；
故答案为：正方形．
变式21．（2023·江西吉安·高一校联考期末）已知空间中两个角，且，若，则 .
【答案】或
【解析】因为两个角，且，
则的两边分别平行，
所以相等或互补，
又，所以或
故答案为：或
变式22．（2023·黑龙江齐齐哈尔·高一校联考期末）已知空间中两个角，，且角与角的两边分别平行，若，则 ．
【答案】或
【解析】根据等角定理知：或，
若，则或.
故答案为：或
【解题方法总结】
空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．
1．（2022•上海）如图正方体中，、、、分别为棱、、、的中点，联结，．空间任意两点、，若线段上不存在点在线段、上，则称两点可视，则下列选项中与点可视的为
A．点B．点C．点D．点
【答案】
【解析】线段上不存在点在线段、上，即直线与线段、不相交，
因此所求与可视的点，即求哪条线段不与线段、相交，
对选项，如图，连接、、，因为、分别为、的中点，
易证，故、、、四点共面，与相交，错误；
对、选项，如图，连接、，易证、、、四点共面，
故、都与相交，、错误；
对选项，连接，由选项分析知、、、四点共面记为平面，
平面，平面，且平面，点，
与为异面直线，
同理由，选项的分析知、、、四点共面记为平面，
平面，平面，且平面，点，
与为异面直线，
故与，都没有公共点，选项正确．
故选：．
2．（2023•上海）如图所示，在正方体中，点为边上的动点，则下列直线中，始终与直线异面的是
A．B．C．D．
【答案】
【解析】对于，当是的中点时，与是相交直线；
对于，根据异面直线的定义知，与是异面直线；
对于，当点与重合时，与是平行直线；
对于，当点与重合时，与是相交直线．
故选：．
3．（2021•乙卷）在正方体中，为的中点，则直线与所成的角为
A．B．C．D．
【答案】
【解析】解法一：，是直线与所成的角（或所成角的补角），
设正方体的棱长为2，
则，，，
，
，
直线与所成的角为．
解法二：，直线与所成角为，
在正△中，是的平分线，
．
直线与所成的角为．
故选：．
考点要求
考题统计
考情分析
（1）借助长方体，在直观认识空间点、直线、平面的位置关系的基础上，抽象出空间点、直线、平面的位置关系的定义．
（2）了解四个基本事实和一个定理，并能应用定理解决问题．
2023年上海卷第15题，5分
2022年上海卷第15题，5分
2022年I卷第9题，5分
2021年乙卷（文）第10题，5分
本节内容是高考命题的热点，重点关注异面直线的判定和成角问题、空间点线面的位置关系问题．对于空间几何体的点、线、面的位置关系，除了题目难度逐步提升，还增加了截面问题，对考生的空间想象能力要求有所提升，需要考生有更强大的逻辑推理能力．
位置关系
相交（共面）
平行（共面）
异面
图形
符号
a∥b
公共点个数
1
0
0
特征
两条相交直线确定一个平面
两条平行直线确定一个平面
两条异面直线不同在如何一个平面内
位置关系
包含（面内线）
相交（面外线）
平行（面外线）
图形
符号
∥
公共点个数
无数个
1
0
位置关系
平行
相交（但不垂直）
垂直
图形
符号
∥
，
公共点个数
0
无数个公共点且都在唯一的一条直线上
无数个公共点且都在唯一的一条直线上