（广东专用）中考数学三轮考前冲刺押题练习第17题 统计与概率（2份，原卷版+解析版）

这是一份（广东专用）中考数学三轮考前冲刺押题练习第17题 统计与概率（2份，原卷版+解析版），文件包含广东专用中考数学三轮考前冲刺押题练习第17题统计与概率原卷版doc、广东专用中考数学三轮考前冲刺押题练习第17题统计与概率解析版doc等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。

广东中考数学对统计与概率知识的考查要求还是以基础为主，近几年一般是以第17-~18题进行考查，一般难度不大，要求考生熟练掌握与统计与概率的基础知识．纵观近几年的中考考试题，题目比较贴近生活题材，知识点主要考查以下两个方面：一是考查具体求数量或圆心角度与补全统计图；二是考查用树状图或列表法计算概率．
在备考此类题型时，考生需要掌握中位数、用样本估计总体、扇形统计图、条形统计图，等相关知识，同时也能用树状图或列表法求相应的概率。解题的关键是明确题意，利用数形结合的思想解答问题．
1．（2020·广东·统考中考真题）某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生选且只能选其中一个等级．随机抽取了120名学生的有效问卷，数据整理如下：
（1）求的值；
（2）若该校有学生1800人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？
2．（2022·广东广州·统考中考真题）某校在九年级学生中随机抽取了若干名学生参加“平均每天体育运动时间”的调查，根据调查结果绘制了如下不完整的频数分布表和频数分布直方图．
频数分布表
请根据图表中的信息解答下列问题：
(1)频数分布表中的=________，=________，=________；
(2)请补全频数分布直方图；
(3)若该校九年级共有480名学生，试估计该校九年级学生平均每天体育运动时间不低于120 min的学生人数．
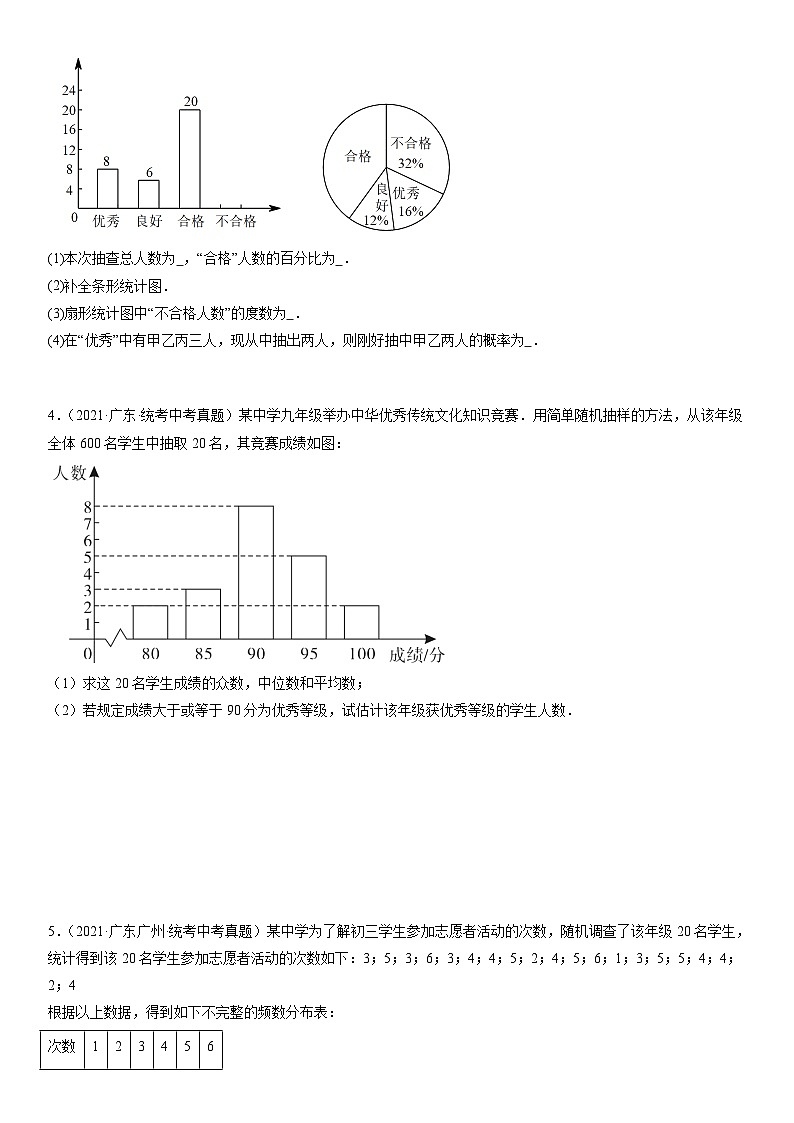
3．（2022·广东深圳·统考中考真题）某工厂进行厂长选拔，从中抽出一部分人进行筛选，其中有“优秀”，“良好”，“合格”，“不合格”．
(1)本次抽查总人数为 ，“合格”人数的百分比为 ．
(2)补全条形统计图．
(3)扇形统计图中“不合格人数”的度数为 ．
(4)在“优秀”中有甲乙丙三人，现从中抽出两人，则刚好抽中甲乙两人的概率为 ．
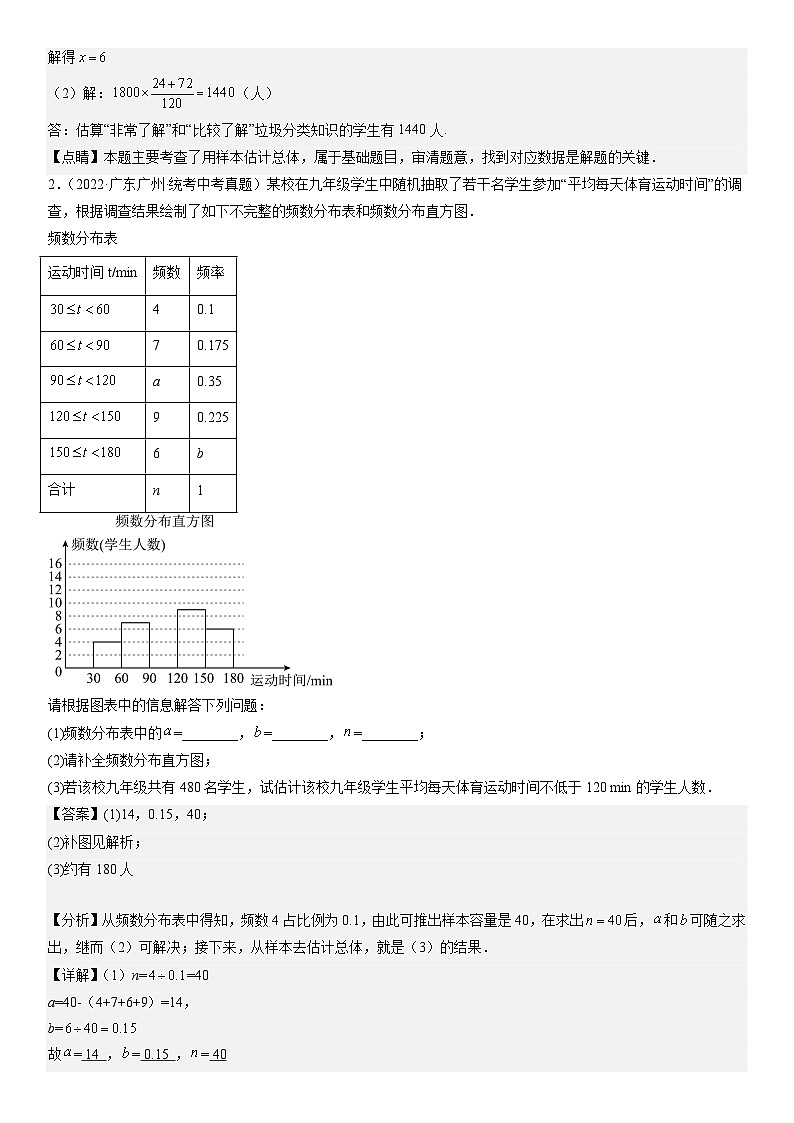
4．（2021·广东·统考中考真题）某中学九年级举办中华优秀传统文化知识竞赛．用简单随机抽样的方法，从该年级全体600名学生中抽取20名，其竞赛成绩如图：
（1）求这20名学生成绩的众数，中位数和平均数；
（2）若规定成绩大于或等于90分为优秀等级，试估计该年级获优秀等级的学生人数．
5．（2021·广东广州·统考中考真题）某中学为了解初三学生参加志愿者活动的次数，随机调查了该年级20名学生，统计得到该20名学生参加志愿者活动的次数如下：3；5；3；6；3；4；4；5；2；4；5；6；1；3；5；5；4；4；2；4
根据以上数据，得到如下不完整的频数分布表：
（1）表格中的________，________；
（2）在这次调查中，参加志愿者活动的次数的众数为________，中位数为________；
（3）若该校初三年级共有300名学生，根据调查统计结果，估计该校初三年级学生参加志愿者活动的次数为4次的人数．
6．（2020·广东广州·统考中考真题）为了更好地解决养老问题，某服务中心引入优质社会资源为甲，乙两个社区共30名老人提供居家养老服务，收集得到这30名老人的年龄（单位：岁）如下：
根据以上信息解答下列问题：
（1）求甲社区老人年龄的中位数和众数；
（2）现从两个社区年龄在70岁以下的4名老人中随机抽取2名了解居家养老服务情况，求这2名老人恰好来自同一个社区的概率．
7．（2023·广东珠海·校考一模）本月初我市市区某校九年级学生进行一次体育模拟测试，将目标效果测试中第二类选考项目（足球运球、篮球运球、排球垫球任选一项）的情况进行统计，并将统计结果绘制成统计图，请你结合图中所给信息解答下列问题：
(1)学校参加本次测试的人数有 人，参加“排球垫球”测试的人数有 人，“篮球运球”的中位数落在 等级；
(2)今年参加体育中考的人数约为万人，你能否估计今年全市选择“篮球运球”的考生会有多少人？若能，求出其人数；若不能，请说明理由；
(3)学校准备从“排球垫球”和“篮球运球”较好的两男两女四名学生中，随机抽取两名学生为全校学生演示动作，请用列表法或画树状图法求恰好抽取到一名男生和一名女生的概率．
8．（2023·广东深圳·校联考模拟预测）2022年4月15日是第七个全民国家安全教育日，某校七、八年级举行了一次国家安全知识竞赛，经过评比后，七年级的两名学生（用，表示）和八年级的两名学生（用，表示）获得优秀奖．
(1)从获得优秀奖的学生中随机抽取一名分享经验，恰好抽到七年级学生的概率是_________．
(2)从获得优秀奖的学生中随机抽取两名分享经验，请用列表法或画树状图法，求抽取的两名学生恰好一名来自七年级、一名来自八年级的概率．
9．（2022·广东江门·统考模拟预测）某校在宣传“中华民族大团结”活动中，采用四种宣传形式：A．器乐，B．舞蹈，C．朗通，D．唱歌．学校就宣传形式对学生进行了抽样调查，每名学生从中选择并且只能选择一种最喜欢的，并将调查结果绘制成了如下两幅不完整的统计图．
请结合题图中所给信息，解答下列问题：
(1)本次调查的学生共有__________人；
(2)补全条形统计图；
(3)该校共有3600名学生，请估计喜欢唱歌的学生有多少人？
(4)某班在最喜欢“器乐”的学生中，有甲、乙、丙、丁四位学生表现优秀，现从这四位学生中随机选出两名学生参加学校的器乐队，请用列表或画树状图法求被选取的两人恰好是甲和乙的概率．
10．（2023·广东深圳·校联考二模）月日是“世界血友病日”，某高校开展义务献血活动，经过检测，献血者血型有“”四种类型，随机抽取部分献血结果统计，根据结果制作如图两幅不完整统计图表：
血型统计表
(1)本次随机抽取献血者人数为_________人，图中_________；
(2)补全表中的数据；
(3)若该高校总共有万名学生，估计其中型血的学生有____________人．
(4)现有个自愿献血者，人为型，人为型，人为型，若在人中随机挑选人，利用树状图或列表法求两人血型均为型的概率．
11．（2023·广东深圳·统考模拟预测）某中学为了丰富学生的校园体育锻炼生活，决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用，因此学校随机抽取了部分同学就兴趣爱好进行调查，将收集的数据整理并绘制成下列两幅统计图，请根据图中的信息，完成下列问题：
(1)学校这次调查共抽取了 名学生；
(2)请补全条形统计图；
(3)在扇形统计图中，羽毛球部分所占的圆心角是 ；
(4)设该校共有学生1200名，请你估计该校有多少名学生喜欢跳绳？
12．（2023·广东珠海·统考一模）我校九年级数学兴趣小组的同学调查了若干名家长对“周末学生回家玩手机”现象的看法，通过统计整理并制作了如图的统计图．
(1)接受这次调查的家长人数为 ___________人；
(2)在扇形统计图中，“不赞同”的家长部分所对应的扇形圆心角大小为 ___________；
(3)表示“无所谓”的家长人数为 ___________人；
(4)在四名（三男一女）持赞同意见的家长当中随机抽查了两名，利用树形图或列表方式求恰好抽到一男一女家长的概率．
13．（2021·广东东莞·东莞市茶山中学校考二模）为了了解全校1500名学生对学校设置的篮球、羽毛球、乒乓球、踢毽子、跳绳共5项体育活动的喜爱情况，在全校范围内随机抽查部分学生，对他们喜爱的体育项目（每人只选一项）进行了问卷调查，将统计数据绘制成如图两幅不完整统计图，请根据图中提供的信息解答下列各题．
(1) ，这次共抽取了 名学生进行调查；并补全条形图；
(2)请你估计该校约有 名学生喜爱打篮球；
(3)现学校准备从喜欢跳绳活动的4人（三男一女）中随机选取2人进行体能测试，请利用列表或画树状图的方法，求抽到一男一女学生的概率是多少？
14．（2023·广东深圳·深圳市南山外国语学校校联考二模）随着时代发展，人们乘坐公交车支付车票的方式更加多样、便捷．某校数学实践小组设计了一份公交车票支付方式调查问卷，要求每位被调查人选且只选一种最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图．
根据所给的信息解答下列问题；
(1)这次活动共调查了______人；在扇形统计图中表示“微信”支付的扇形圆心角的度数为______；
(2)将条形统计图补充完整；
(3)小明和小亮都没有公交卡，在乘车中，想从“微信”“支付宝”“现金”“云闪付”四种支付方式中选一种方式进行支付，请用画树状图或列表格的方法，求出两人恰好选择同一种支付方式的概率．
15．（2023·广东深圳·深圳大学附属中学校考一模）“双减”政策的实施，不仅减轻了学生的负担，也减轻了家长的负担，回归了教育的初衷．某校计划在某个班向家长展示“双减”背景下的课堂教学活动，用于展开活动的备选班级共5个，其中有2个为八年级班级（分别用A、B表示），3个为九年级班级（分别用C、D、E表示），由于报名参加观摩课堂教学活动的家长较多，学校计划分两周进行，第一周先从这5个备选班级中任意选择一个开展活动，第二周再从剩下的四个备选班级中任意选择一个开展活动．
(1)第一周选择的是八年级班级的概率为______；
(2)请用列表法或画树状图的方法求两次选中的既有八年级班级又有九年级班级的概率．
16．（2023·广东东莞·东莞中学南城学校校联考一模）目前我市“校园手机”现象越来越受到社会的关注，针对这种现象，某校初三班数学兴趣小组的同学随机调查了若干名家长对“中学生带手机的”的态度态度分为：无所谓；基本赞成；赞成；反对并将调查结果绘制成频数折线统计图和扇形统计图不完整请根据图中提供的信息，解答下列问题：
(1)求出图中扇形所对的圆心角的度数为______ 度，并将图补充完整；
(2)根据抽样调查结果，请你估计该校名中学生家长中持反对态度的人数．
17．（2023·广东揭阳·统考一模）为庆祝神舟十五号载人飞船发射取得圆满成功，某校举办了航天航空科技体验活动，内容有四项：A．聆听航天科普讲座；B．参加航天梦想营；C．参观航天科技展；D．制作航天火箭模型．每位同学从中随机选择一项参加．
(1)该校小红同学选择“参观航天科技展”的概率是______；
(2)用列表或画树状图的方法，求该校小明同学和小亮同学同时选择“参加航天梦想营”的概率．
18．（2023·广东东莞·虎门五中校联考一模）中华文化渊源流长，在文学方面，《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表，被称为“四大古典名著”，现东莞某中学为了了解学生对四大古典名著的阅读情况，就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查，根据调查结果绘制成如下尚不完整的统计图．
请根据以上信息，解决下列问题：
(1)本次调查所得数据的众数是______部，中位数是______部；将条形统计图补充完整
(2)这项被调查的总人数是多少人？
(3)扇形统计图中“4部”所在扇形的圆心角的度数是多少？
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读，请用列表或画树出图的方法求他们恰好选中同一名著概率．
19．（2023·广东深圳·二模）2022年冬奥会和冬残奥会在我国举行．如图，冬奥会的会徽和吉祥物为“冬梦”、“冰墩墩”，冬残奥会的会徽和吉祥物为“飞跃”、“雪容融”，将4张正面分别印有以上图案的卡片随机分成甲、乙两组，每组2张．
(1)“冰墩墩”在甲组的概率是______；
(2)求每组的2张卡片恰是会徽和对应吉祥物的概率，
20．（2023·广东深圳·校考一模）北京2022年冬奥会的成功举办，激起了同学们对冰雪运动的广泛兴趣．某校对部分学生进行了“我最喜欢的冰雪运动项目”的问卷调查，要求参加问卷调查的学生在冰球、冰壶、短道速滑、高山滑雪四项冰雪运动项目中选且只选一项．根据调查结果，绘制了如下两幅不完整的统计图．根据图中信息，解答下列问题：
(1)求参加这次调查的学生总人数和选择“冰壶”的学生人数；
(2)求扇形统计图中“高山滑雪”对应扇形的圆心角度数；
(3)该校共有1200名学生，请你估算其中最喜欢“短道速滑”的学生人数．
21．（2023·广东东莞·校考三模）“校园安全”受到全社会的广泛关注，卧龙中学对部分学生就校园安全知识的了解程度，采用随机抽样调查的方式，并根据收集到的信息进行统计，绘制了两幅尚不完整的统计图，如图所示，请根据统计图中所提供的信息解答下列问题：
（1）接受问卷调查的学生共有______人，扇形统计图中“基本了解”部分所对应扇形的圆心角为_____度；
（2）请补全条形统计图；
（3）若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛，请用树状图或列表法求出恰好抽到1个男生和1个女生的概率．
22．（2023·广东珠海·校考一模）2020年，新冠肺炎疫情突如其来，各大中小幼学校延期开学，实行“停课不停教不停学”，网络直播教学成为其中最常见的教学方式，某区为了解九年级老师使用线上授课软件情况，在4月份某天随机抽查了若干名老师进行调查，其中A表示“一起中学”，B表示“腾讯会议”，C表示“腾讯课堂”，D表示“QQ群课堂”，E表示“钉钉”，现将调查结果绘制成两种不完整的统计图表：
请根据图表中的信息解答下列问题：
（1）b＝ ，并将频数分布直方图补充完整；
（2）已知该区共有九年级老师500人，请你估计该区使用“QQ群课堂”有多少人？
（3）该区计划在A组随机抽取两人了解使用情况，已知A组有理科老师2人，文科老师1人，请用列举法求出抽取两名老师都是理科老师的概率．
23．（2023·广东惠州·统考一模）为帮助学生养成热爱美、发现美的艺术素养，某校开展了“一人一艺”的艺术选修课活动．学生根据自己的喜好选择一门艺术项目（：书法，：绘画，：摄影，：泥塑，：剪纸），张老师随机对该校部分学生的选课情况进行调查后，制成了两幅不完整的统计图（如图所示）．根据统计图信息完成下列问题：
(1)张老师调查的学生人数是______，其中选择“泥塑”选修课的人数是______，“剪纸”项目在扇形统计图中圆心角的度数为______；若该校共有学生1000名，请估计全校选修“绘画”的学生人数约是______．
(2)现有4名学生，其中2人选修书法，1人选修绘画，1人选修摄影，张老师要从这4人中任选2人了解他们对艺术选修课的看法，请用画树状图或列表的方法（用表示），求所选2人都是选修“书法”的概率．
24．（2023·广东东莞·校考一模）为提高学生的综合素养，某校开设了四个兴趣小组，A“健美操”、B“跳绳”、C“剪纸”、D“书法”为了了解学生对每个兴趣小组的喜爱情况，随机抽取了部分同学进行调查，并将调查结果绘制出上面不完整的统计图，请结合图中的信息解答下列问题：
(1)本次共调查了______名学生；并将条形统计图补充完整；
(2)C组所对应的扇形圆心角为_______度；
(3)若该校共有学生1400人，则估计该校喜欢跳绳的学生人数约是__________；
(4)现选出了4名跳绳成绩最好的学生，其中有1名男生和3名女生．要从这4名学生中任意抽取2名学生去参加比赛，请用列表法或画树状图法，求刚好抽到1名男生与1名女生的概率．
25．（2023·广东深圳·统考二模）“走进数学世界，感受完美生活．”为增进全体学生对数学文化的了解，临海学校组织了趣味数学知识竞赛，随机抽取若干名学生的成绩，对数据进行整理和分析，现将抽取的学生成绩用（分）表示，并将调查数据分成四组：A．，B．，C．，D．，其中组分数段内，所有学生得分各不相同，组学生的成绩分别为：86、86、88、86、83、86．
根据调查数据绘制了以下不完整的统计图：
根据图中信息回答下列问题：
(1)本次共抽查了__________名学生，请补全条形统计图；
(2)扇形统计图中，组所对应的圆心角的度数为__________；
(3)本次抽查的学生成绩的众数为__________，中位数为__________；
(4)竞赛成绩超过80分视作优秀，若该校有2400名学生，根据抽样调查结果，估计该校有__________名学生获得优秀．
26．（2023·广东江门·统考一模）为了解市民对江门市创建全国文明城市工作的满意程度，某学校数学兴趣小组在骏景湾小区内进行了调查统计．将调查结果分为不满意，一般，满意，非常满意四类，回收、整理好全部问卷后，有意隐去了一些数据，得到不完整的统计图表，设计了一道数学题．
请结合图中的信息，解决下列问题：
(1)请求出接受问卷调查的人数，并补全条形统计图；
(2)请求出扇形统计图中“满意”部分的圆心角度数；
(3)该兴趣小组准备从调查结果为“不满意”的位市民中随机选择位进行回访，已知这位市民中有位男性，位女性．请用画树状图或列表的方法求出选择回访的市民为“一男一女”的概率．
等级
非常了解
比较了解
基本了解
不太了解
人数（人）
24
72
18
运动时间t/min
频数
频率
4
0.1
7
0.175
a
0.35
9
0.225
6
b
合计
n
1
次数
1
2
3
4
5
6
人数
1
2
a
6
b
2
甲社区
67
68
73
75
76
78
80
82
83
84
85
85
90
92
95
乙社区
66
69
72
74
75
78
80
81
85
85
88
89
91
96
98
血型
人数
组别
使用人数（人）
占调查人数的百分率
A
3
5%
B
12
20%
C
a
35%
D
15
c
E
b
15%