（浙江专用）中考数学二轮培优压轴题练习专题05 以三角形为载体的几何综合问题（2份，原卷版+解析版）

这是一份（浙江专用）中考数学二轮培优压轴题练习专题05 以三角形为载体的几何综合问题（2份，原卷版+解析版），文件包含浙江专用中考数学二轮培优压轴题练习专题05以三角形为载体的几何综合问题原卷版doc、浙江专用中考数学二轮培优压轴题练习专题05以三角形为载体的几何综合问题解析版doc等2份试卷配套教学资源，其中试卷共59页， 欢迎下载使用。
【考点1】关于三角形角度计算与证明的综合问题
【例1】（2019•衢州）“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动、C点固定，OC＝CD＝DE，点D、E可在槽中滑动．若∠BDE＝75°，则∠CDE的度数是（ ）
A．60°B．65°C．75°D．80°
【例2】（2019•杭州）如图，在△ABC中，AC＜AB＜BC．
（1）已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：∠APC＝2∠B．
（2）以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ．若∠AQC＝3∠B，求∠B的度数．
【考点2】关于三角形的线段计算综合问题
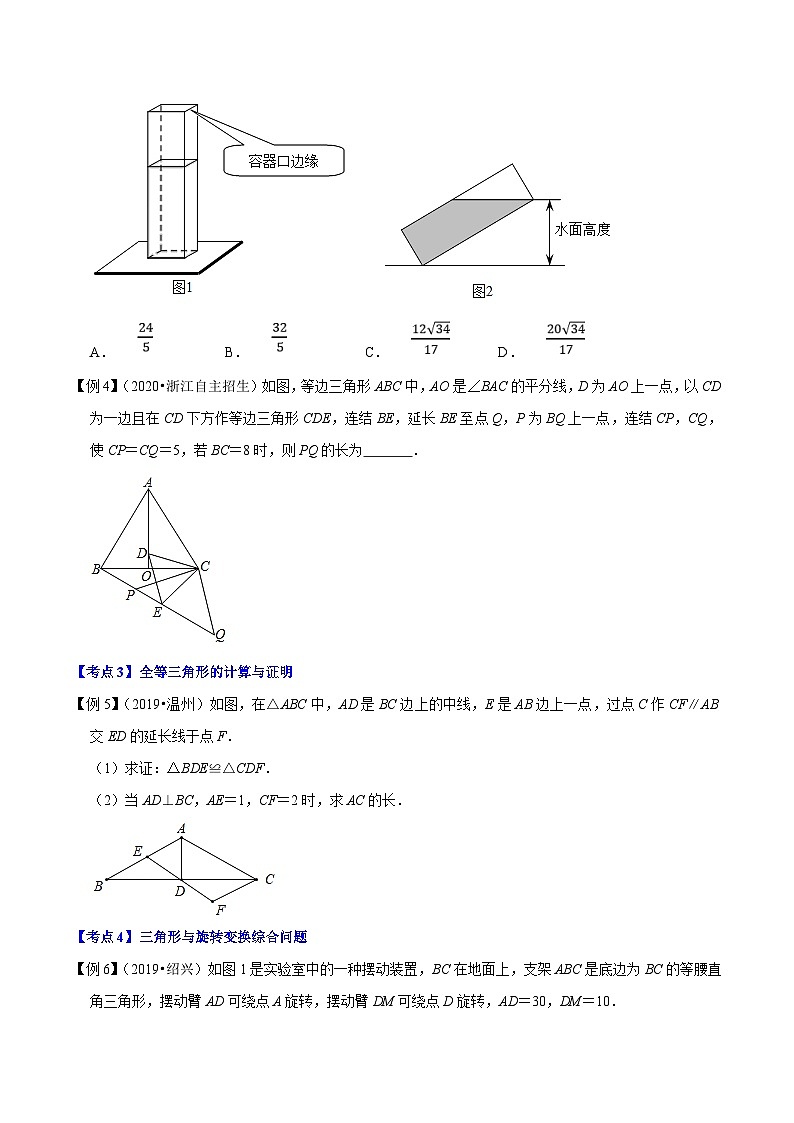
【例3】（2019•绍兴）如图1，长、宽均为3，高为8的长方体容器，放置在水平桌面上，里面盛有水，水面高为6，绕底面一棱进行旋转倾斜后，水面恰好触到容器口边缘，图2是此时的示意图，则图2中水面高度为（ ）
A．B．C．D．
【例4】（2020•浙江自主招生）如图，等边三角形ABC中，AO是∠BAC的平分线，D为AO上一点，以CD为一边且在CD下方作等边三角形CDE，连结BE，延长BE至点Q，P为BQ上一点，连结CP，CQ，使CP＝CQ＝5，若BC＝8时，则PQ的长为 ．
【考点3】全等三角形的计算与证明
【例5】（2019•温州）如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F．
（1）求证：△BDE≌△CDF．
（2）当AD⊥BC，AE＝1，CF＝2时，求AC的长．
【考点4】三角形与旋转变换综合问题
【例6】（2019•绍兴）如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD＝30，DM＝10．
（1）在旋转过程中，
①当A，D，M三点在同一直线上时，求AM的长．
②当A，D，M三点为同一直角三角形的顶点时，求AM的长．
（2）若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D1转到其内的点D2处，连结D1D2，如图2，此时∠AD2C＝135°，CD2＝60，求BD2的长．
【考点5】以三角形为载体的几何综合探究问题
【例7】（2018•舟山）已知，△ABC中，∠B＝∠C，P是BC边上一点，作∠CPE＝∠BPF，分别交边AC，AB于点E，F．
（1）若∠CPE＝∠C（如图1），求证：PE+PF＝AB．
（2）若∠CPE≠∠C，过点B作∠CBD＝∠CPE，交CA（或CA的延长线）于点D．试猜想：线段PE，PF和BD之间的数量关系，并就∠CPE＞∠C情形（如图2）说明理由．
（3）若点F与A重合（如图3），∠C＝27°，且PA＝AE．
①求∠CPE的度数；
②设PB＝a，PA＝b，AB＝c，试证明：b．
【例8】（2018•台州）如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点D，E分别在AC，BC上，且CD＝CE．
（1）如图1，求证：∠CAE＝∠CBD；
（2）如图2，F是BD的中点，求证：AE⊥CF；
（3）如图3，F，G分别是BD，AE的中点，若AC＝2，CE＝1，求△CGF的面积．
【考点6】以三角形为载体的几何阅读创新题
【例9】（2018•绍兴）数学课上，张老师举了下面的例题：
例1 等腰三角形ABC中，∠A＝110°，求∠B的度数．（答案：35°）
例2 等腰三角形ABC中，∠A＝40°，求∠B的度数，（答案：40°或70°或100°）
张老师启发同学们进行变式，小敏编了如下一题：
变式 等腰三角形ABC中，∠A＝80°，求∠B的度数．
（1）请你解答以上的变式题．
（2）解（1）后，小敏发现，∠A的度数不同，得到∠B的度数的个数也可能不同，如果在等腰三角形ABC中，设∠A＝x°，当∠B有三个不同的度数时，请你探索x的取值范围．
一．选择题（共5小题）
1．（2020•衢州模拟）在我国古代数学著作《九章算术》“勾股”章中有一题：“今有开门去阃（kǔn）一尺，不合二寸，问门广几何？”大意是说：如图，推开双门（AD和BC），门边缘D，C两点到门槛AB的距离为1尺（1尺＝10寸），双门间的缝隙CD为2寸，那么门的宽度（两扇门的和）AB为（ ）
A．103寸B．102寸C．101寸D．100寸
2．（2020•拱墅区校级一模）如图，在△ABC中，∠C＝90°，D是BC边上一点，∠ADC＝3∠BAD，BD＝4，DC＝3．则AB的值为（ ）
A．5+3B．2+2C．7D．
3．（2020•温州模拟）如图，已知∠ACB＝∠DBC，添加以下条件，不能判定△ABC≌△DCB的是（ ）
A．∠ABC＝∠DCBB．∠ABD＝∠DCAC．AC＝DBD．AB＝DC
4．（2019•周村区一模）如图，在△ABC中，∠B＝50°，∠C＝30°，分别以点A和点C为圆心，大于AC的长为半径画弧，两弧相交于点M，N，作直线MN交BC于点D，连接AD，则∠BAD的度数为（ ）
A．50°B．60°C．70°D．80°
5．（2020•黄岩区模拟）如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P，BE＝BC，PB与CE交于点H，PG∥AD交BC于F，交AB于G，连接CP．下列结论：①∠ACB＝2∠APB；②S△PAC：S△PAB＝AC：AB；③BP垂直平分CE；④∠PCF＝∠CPF．其中，正确的有（ ）
A．1个B．2个C．3个D．4个
二．填空题（共4小题）
6．（2020•温州模拟）如图，已知OP平分∠AOB，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．CP，PD＝6．如果点M是OP的中点，则DM的长是 ．
7．（2020•温岭市校级一模）在半径为2的⊙O中，弦AB＝2，连接OA，OB．在直线OB上取一点K，使tan∠BAK，则△OAK的面积为 ．
8．（2020•萧山区一模）如图，CE、BF分别是△ABC的高线，连接EF，EF＝6，BC＝10，D、G分别是EF、BC的中点，则DG的长为 ．
9．（2019•海宁市二模）如图，四边形ABCD中，∠ABC＝∠BCD＝90°，AB＝1，AE⊥AD，交BC于点E，EA平分∠BED．
（1）CD的长是 ；
（2）当点F是AC中点时，四边形ABCD的周长是 ．
三．解答题（共11小题）
10．（2020•拱墅区校级一模）在△ABC和△DBE中，CA＝CB，EB＝ED，点D在AC上．
（1）如图1，若∠ABC＝∠DBE＝60°，求证：∠ECB＝∠A；
（2）如图2，设BC与DE交于点F．当∠ABC＝∠DBE＝45°时，求证：CE∥AB；
（3）在（2）的条件下，若tan∠DEC时，求的值．
11．（2020•天台县模拟）某校组织数学兴趣探究活动，爱思考的小实同学在探究两条直线的位置关系查阅资料时发现，两条中线互相垂直的三角形称为“中垂三角形”．如图1、图2、图3中，AF、BE是△ABC的中线，AF⊥BE于点P，像△ABC这样的三角形均称为“中垂三角形”．
【特例探究】
（1）如图1，当∠PAB＝45°，AB＝6时，AC＝ ，BC＝ ；
如图2，当sin∠PAB，AB＝4时，AC＝ ，BC＝ ；
【归纳证明】
（2）请你观察（1）中的计算结果，猜想AB2、BC2、AC2三者之间的关系，用等式表示出来，并利用图3证明你的结论．
【拓展证明】
（3）如图4，在△ABC中，AB＝4，BC＝2，D、E、F分别是边AB、AC、BC的中点，连结DE并延长至G，使得GE＝DE，连结BG，当BG⊥AC于点M时，求GF的长．
12．（2020•拱墅区校级模拟）如图，在Rt△ABC中，∠CAB＝90°，AF为BC边上的中线，DE经过△ABC的重心G，且∠ADE＝∠C．
（1）问：线段AG是△ADE的高线还是中线？请说明理由．
（2）若AB＝6，AC＝8，求AD的长．
13．（2020•温州模拟）如图，△ABC中，∠ABC＝∠ACB，点D在BC所在的直线上，点E在射线AC上，且AD＝AE，连接DE．
（1）如图①，若∠B＝∠C＝35°，∠BAD＝80°，求∠CDE的度数；
（2）如图②，若∠ABC＝∠ACB＝75°，∠CDE＝18°，求∠BAD的度数；
（3）当点D在直线BC上（不与点B、C重合）运动时，试探究∠BAD与∠CDE的数量关系，并说明理由．
14．（2020•上城区模拟）如图，△ABC中，∠ACB＝90°，AB＝5cm，BC＝3cm，若点P从点A出发，以每秒2cm的速度沿折线A﹣C﹣B﹣A运动，设运动时间为t秒（t＞0）．
（1）若点P在AC上，且满足PA＝PB时，求出此时t的值；
（2）若点P恰好在∠BAC的角平分线上，求t的值；
（3）在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．
15．（2019•杭州模拟）定义：若一个三角形一条边上的高等于这条边长的一半，则称该三角形为“半高”三角形，这条高称为“半高”．
（1）如图1，△ABC中，∠ACB＝90°，BC＝2AC，点P在AB上，PD⊥AC于点D，PE⊥BC于点E，连接BD，DE求证：△BDE是“半高”三角形；
（2）如图2，△ABC是“半高”三角形，且BC边上的高是“半高”，点P在AB上，PQ∥BC交AC于点Q，PM⊥BC于点M，QN⊥BC于点N．
①请探究BM，PM，CN之间的等量关系，并说明理由；
②若△ABC的面积等于16，求MQ的最小值．
16．（2019•南浔区二模）（1）尝试探究
如图1，等腰Rt△ABC的两个顶点B，C在直线MN上，点D是直线MN上一个动点（点D在点C的右边），BC＝3，BD＝m，在△ABC同侧作等腰Rt△ADE，∠ABC＝∠ADE＝90°，EF⊥MN于点F，连接CE．
①求DF的长；
②在判断AC⊥CE是否成立时，小明同学发现可以由以下两种思路解决此问题：
思路一：先证CF＝EF，求出∠ECF＝45°，从而证得结论成立．
思路二：先求DF，EF的长，再求CF的长，然后证AC2+CE2＝AE2，从而证得结论成立．
请你任选一种思路，完整地书写本小题的证明过程．（如用两种方法作答，则以第一种方法评分）
（2）拓展探究
将（1）中的两个等腰直角三角形都改为有一个角为30°的直角三角形，如图2，∠ABC＝∠ADE＝90°，∠BAC＝∠DAE＝30°，BC＝3，BD＝m，当4≤m≤6时，求CE长的范围．
17．（2019•瑞安市三模）如图，在等腰△ABC中，AB＝BC，点D是AC边的中点，延长BD至点E，使得DE＝BD，连结CE．
（1）求证：△ABD≌△CED．
（2）当BC＝5，CD＝3时，求△BCE的周长．
18．（2019•黄岩区二模）如图，△ABC和△ADE是两个不全等的等腰直角三角形，其中点B与点D是直角顶点，现固定△ABC，而将△ADE绕点A在平面内旋转．
（1）如图1，当点D在CA延长线上时，点M为EC的中点，求证：△DMB是等腰三角形．
（2）如图2，当点E在CA延长线上时，M是EC上一点，若△DMB是等腰直角三角形，∠DMB为直角，求证：点M是EC的中点．
（3）如图3，当△ADE绕点A旋转任意角度时，线段EC上是否都存在点M，使△BMD为等腰直角三角形，若不存在，请举出反例；若存在，请予以证明．
19．（2019•余杭区二模）如图，在正方形ABCD中，点E，F分别在BC，AB上，且DE＝DF，连结AC，分别交DE，DF于点M，N．
（1）求证：△ADF≌△CDE；
（2）设△DMN和△AFN的面积分别为S1和S2；
①若∠ADF＝∠EDF，求S2：S1的值．
②若S2＝2S1，求tan∠ADF．
20．（2019•慈溪市模拟）定义：在一个三角形中，若存在两条边x和y，使得y＝x2，则称此三角形为“平方三角形”，x称为平方边．
（1）“若等边三角形为平方三角形，则面积为是 命题；“有一个角为30°且有一条直角边为2的直角三角形是平方三角形”是 命题；（填“真”或“假”）
（2）若a，b，c是平方三角形的三条边，平方边a＝2，若三角形中存在一个角为60°，求c的值；
（3）如图，在△ABC中，D是BC上一点．
①若∠CAD＝∠B，CD＝1，求证，△ABC是平方三角形；
②若∠C＝90°，BD＝1，AC＝m，CD＝n，求tan∠DAB．（用含m，n的代数式表示）