中考数学二轮复习二次函数重难点练习专题12 二次函数与直角三角形存在性问题（2份，原卷版+解析版）

这是一份中考数学二轮复习二次函数重难点练习专题12 二次函数与直角三角形存在性问题（2份，原卷版+解析版），文件包含中考数学二轮复习二次函数重难点练习专题12二次函数与直角三角形存在性问题原卷版doc、中考数学二轮复习二次函数重难点练习专题12二次函数与直角三角形存在性问题解析版doc等2份试卷配套教学资源，其中试卷共71页， 欢迎下载使用。
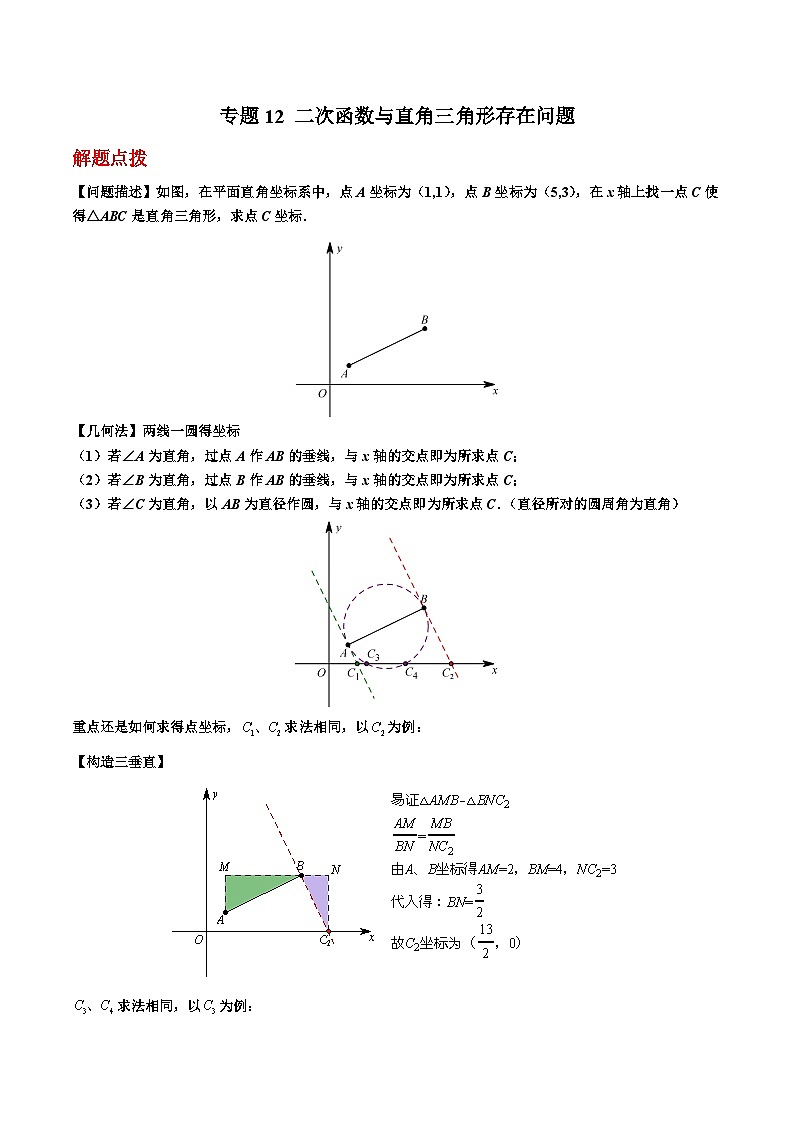
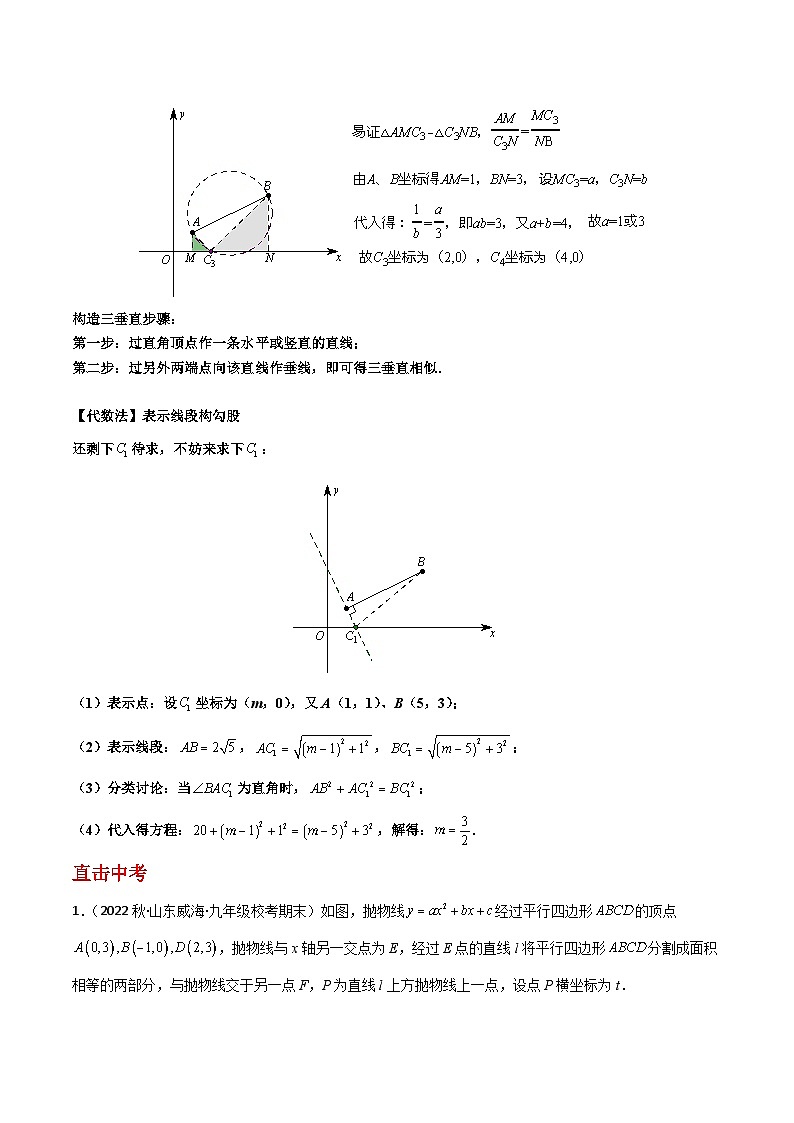
【问题描述】如图，在平面直角坐标系中，点A坐标为（1,1），点B坐标为（5,3），在x轴上找一点C使得△ABC是直角三角形，求点C坐标．
【几何法】两线一圆得坐标
（1）若∠A为直角，过点A作AB的垂线，与x轴的交点即为所求点C；
（2）若∠B为直角，过点B作AB的垂线，与x轴的交点即为所求点C；
（3）若∠C为直角，以AB为直径作圆，与x轴的交点即为所求点C．（直径所对的圆周角为直角）
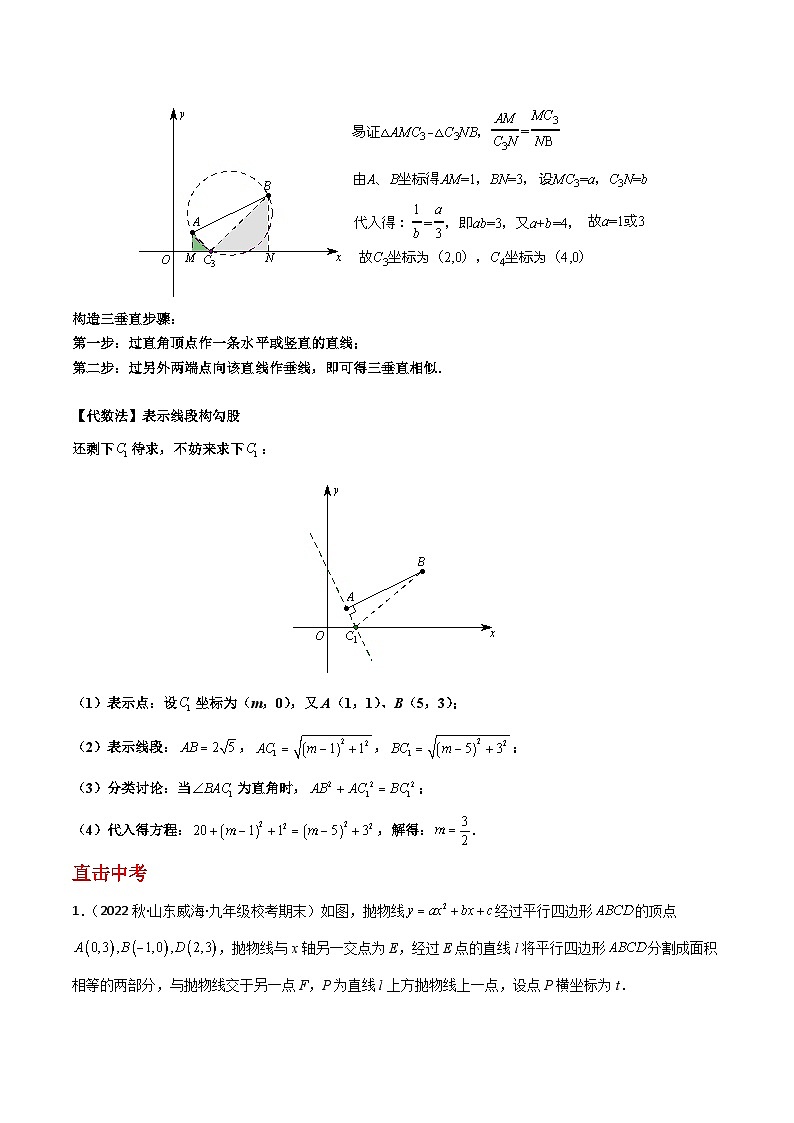
重点还是如何求得点坐标，求法相同，以为例：
【构造三垂直】
求法相同，以为例：
构造三垂直步骤：
第一步：过直角顶点作一条水平或竖直的直线；
第二步：过另外两端点向该直线作垂线，即可得三垂直相似．
【代数法】表示线段构勾股
还剩下待求，不妨来求下：
（1）表示点：设坐标为（m，0），又A（1，1）、B（5，3）；
（2）表示线段：，，；
（3）分类讨论：当为直角时，；
（4）代入得方程：，解得：．
直击中考
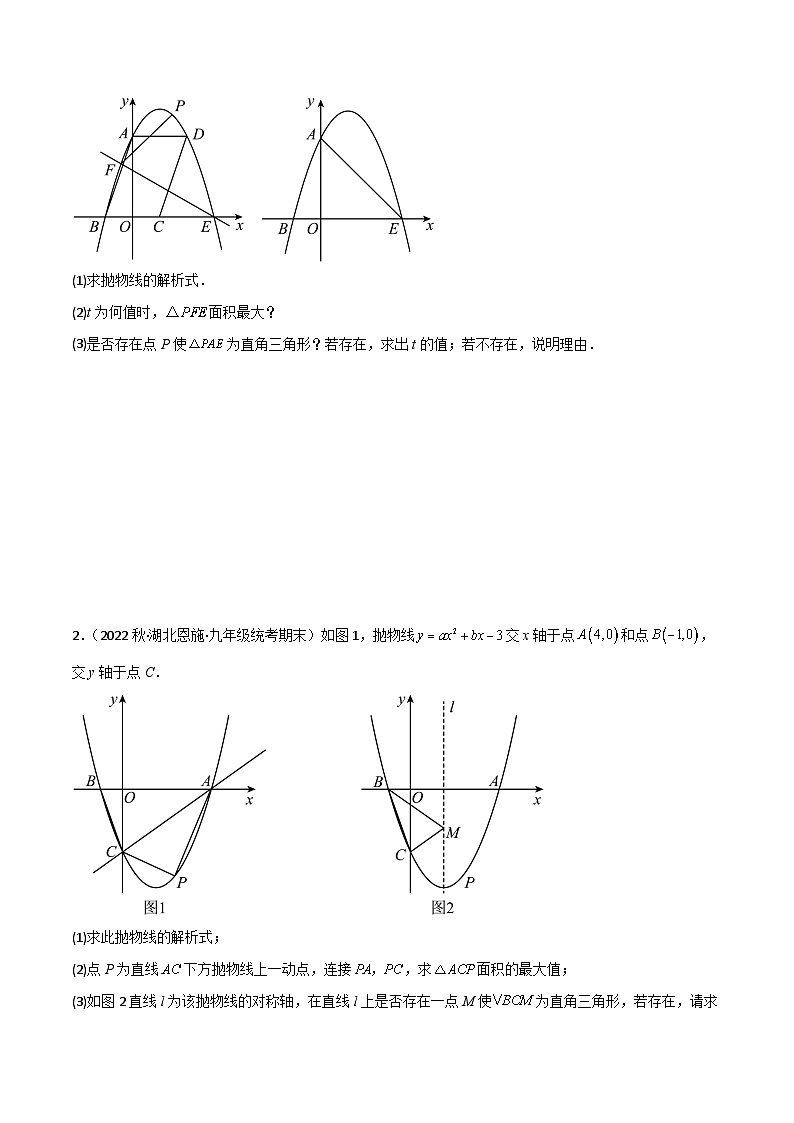
1．（2022秋·山东威海·九年级校考期末）如图，抛物线经过平行四边形的顶点，抛物线与x轴另一交点为E，经过E点的直线l将平行四边形分割成面积相等的两部分，与抛物线交于另一点F，P为直线l上方抛物线上一点，设点P横坐标为t．
(1)求抛物线的解析式．
(2)t为何值时，面积最大？
(3)是否存在点P使为直角三角形？若存在，求出t的值；若不存在，说明理由．
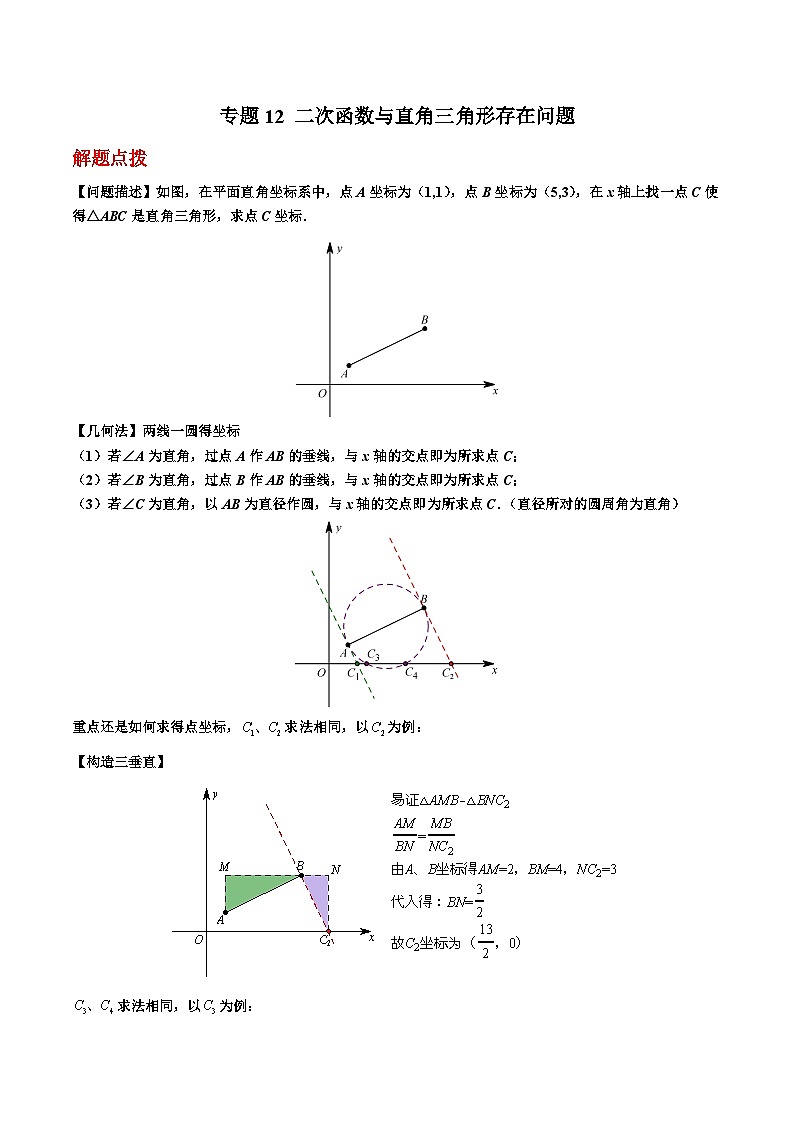
2．（2022秋·湖北恩施·九年级统考期末）如图1，抛物线交x轴于点和点，交y轴于点C．
(1)求此抛物线的解析式；
(2)点P为直线下方抛物线上一动点，连接，求面积的最大值；
(3)如图2直线l为该抛物线的对称轴，在直线l上是否存在一点M使为直角三角形，若存在，请求出点M的坐标，若不存在，请说明理由．
3．（2021秋·广东江门·九年级校考期中）如图，抛物线与x轴交于A、B两点，与y轴交于C点．
(1)直接写出：抛物线顶点M的坐标__________（用含m的代数式表示），A，B的坐标分别是A（__________），B（__________）；
(2)求的面积（用含m的代数式表示）；
(3)是否存在使为直角三角形的抛物线？若存在，请求出，若不存在，请说明理由．
4．（2021秋·陕西榆林·九年级统考期末）如图，抛物线交y轴于点，交x轴于点和点B（点A在点B的左侧）．
(1)求该抛物线的函数表达式；
(2)在抛物线的对称轴上是否存在点P，使点A、B、P构成的三角形是以为斜边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
5．（2022秋·安徽安庆·九年级统考期中）如图，抛物线与轴交于、两点，与轴交于点．
(1)求抛物线的解析式和点和点的坐标；
(2)在轴下方的抛物线上是否存在一点，使四边形的面积最大？若存在，请求出点的坐标；若不存在，请说明理由；
(3)在抛物线上求点，使是以为直角边的直角三角形．
6．（2021秋·广西贵港·九年级统考期末）如图，抛物线经过点．
(1)求抛物线的解析式；
(2)若点P为第三象限内抛物线上的一点，设的面积为3，求点P的坐标；
(3)设抛物线的顶点为D，轴于点E，在轴上是否存在点M，使是以为直角边的直角三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．
7．（2022·广西柳州·统考中考真题）已知抛物线y＝﹣x2+bx+c与x轴交于A（﹣1，0），B（m，0）两点，与y轴交于点C（0，5）．
(1)求b，c，m的值；
(2)如图1，点D是抛物线上位于对称轴右侧的一个动点，且点D在第一象限内，过点D作x轴的平行线交抛物线于点E，作y轴的平行线交x轴于点G，过点E作EF⊥x轴，垂足为点F，当四边形DEFG的周长最大时，求点D的坐标；
(3)如图2，点M是抛物线的顶点，将△MBC沿BC翻折得到△NBC，NB与y轴交于点Q，在对称轴上找一点P，使得△PQB是以QB为直角边的直角三角形，求出所有符合条件的点P的坐标．
8．（2022·四川广安·统考中考真题）如图，在平面直角坐标系中，抛物线（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，－4），点C坐标为（2，0）．
(1)求此抛物线的函数解析式．
(2)点D是直线AB下方抛物线上一个动点，连接AD、BD，探究是否存在点D，使得△ABD的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．
(3)点P为该抛物线对称轴上的动点，使得△PAB为直角三角形，请求出点P的坐标．
9．（2022·辽宁抚顺·统考中考真题）如图，抛物线与x轴交于，B两点，与y轴交于点，点D为x轴上方抛物线上的动点，射线交直线于点E，将射线绕点O逆时针旋转得到射线，交直线于点F，连接．
(1)求抛物线的解析式；
(2)当点D在第二象限且时，求点D的坐标；
(3)当为直角三角形时，请直接写出点D的坐标．
10．（2022·吉林·统考中考真题）如图，在平面直角坐标系中，抛物线（，是常数）经过点，点．点在此抛物线上，其横坐标为．
(1)求此抛物线的解析式；
(2)当点在轴上方时，结合图象，直接写出的取值范围；
(3)若此抛物线在点左侧部分（包括点）的最低点的纵坐标为．
①求的值；
②以为边作等腰直角三角形，当点在此抛物线的对称轴上时，直接写出点的坐标．
11．（2022·山东滨州·统考中考真题）如图，在平面直角坐标系中，抛物线与x轴相交于点A、B（点A在点B的左侧），与y轴相交于点C，连接．
(1)求线段AC的长；
(2)若点Р为该抛物线对称轴上的一个动点，当时，求点P的坐标；
(3)若点M为该抛物线上的一个动点，当为直角三角形时，求点M的坐标．
12．（2019·西藏·统考中考真题）已知：如图，抛物线y＝ax2+bx+3与坐标轴分别交于点A，B（﹣3，0），C（1，0），点P是线段AB上方抛物线上的一个动点，过点P作x轴的垂线，交线段AB于点D，再过点P作PEx轴交抛物线于点E．
(1)求抛物线解析式；
(2)当点P运动到什么位置时，DP的长最大？
(3)是否存在点P使△PDE为等腰直角三角形？若存在，求点P的坐标；若不存在，说明理由．
13．（2021·四川巴中·统考中考真题）已知抛物线y＝ax2+bx+c与x轴交于A(﹣2，0)、B(6，0)两点，与y轴交于点C(0，﹣3)．
（1）求抛物线的表达式；
（2）点P在直线BC下方的抛物线上，连接AP交BC于点M，当最大时，求点P的坐标及的最大值；
（3）在（2）的条件下，过点P作x轴的垂线l，在l上是否存在点D，使BCD是直角三角形，若存在，请直接写出点D的坐标；若不存在，请说明理由．
14．（2021·贵州毕节·统考中考真题）如图，抛物线与轴相交于A，B两点，与y轴相交于点C，对称轴为直线，项点为D，点B的坐标为．
（1）填空：点A的坐标为_________，点D的坐标为_________，抛物线的解析式为_________；
（2）当二次函数的自变量：满足时，函数y的最小值为，求m的值；
（3）P是抛物线对称轴上一动点，是否存在点P，使是以AC为斜边的直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．
15．（2022·江苏无锡·统考一模）如图，在平面直角坐标系中，点O为坐标原点，二次函数的图象与x轴交于A、B（点A在点B左侧）两点，与y轴交于点C，已知点，P点为抛物线的顶点，连接PC，作直线．
(1)点A的坐标为 ；
(2)若射线平分，求二次函数的表达式；
(3)在（2）的条件下，如果点是线段（含A、B）上一个动点，过点D作x轴的垂线，分别交直线和抛物线于E、F两点，当m为何值时，为直角三角形？
16．（2022·广东深圳·校考模拟预测）如图，二次函数的图像与直线y＝x+5的图像交于A，B两点，且两个交点分别在x轴和y轴上，
(1)求二次函数的解析式；
(2)P（a，b）是抛物线上一点，
①当a＞2时，是否存在点P使得△PAB是直角三角形，若存在，求出P点坐标，若不存在，请说明理由；
②当﹣5＜a＜0时，是否存在点P到直线AB有最大距离，若存在，直接写出P点的横坐标，若不存在，请说明理由．
17．（2022·浙江丽水·统考二模）如图，已知抛物线（a≠0）的对称轴为直线x＝﹣1，且抛物线经过A（1，0），C（0，3）两点，与x轴交于点B．
(1)若直线y＝mx+n经过B，C两点，求直线BC和抛物线的解析式；
(2)在抛物线的对称轴x＝﹣1上找一点M，使MA+MC的值最小，求点M的坐标；
(3)设P为抛物线的对称轴x＝﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．