中考数学二轮复习二次函数重难点练习专题25 二次函数与最大角问题（2份，原卷版+解析版）

这是一份中考数学二轮复习二次函数重难点练习专题25 二次函数与最大角问题（2份，原卷版+解析版），文件包含中考数学二轮复习二次函数重难点练习专题25二次函数与最大角问题原卷版doc、中考数学二轮复习二次函数重难点练习专题25二次函数与最大角问题解析版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
【问题描述】
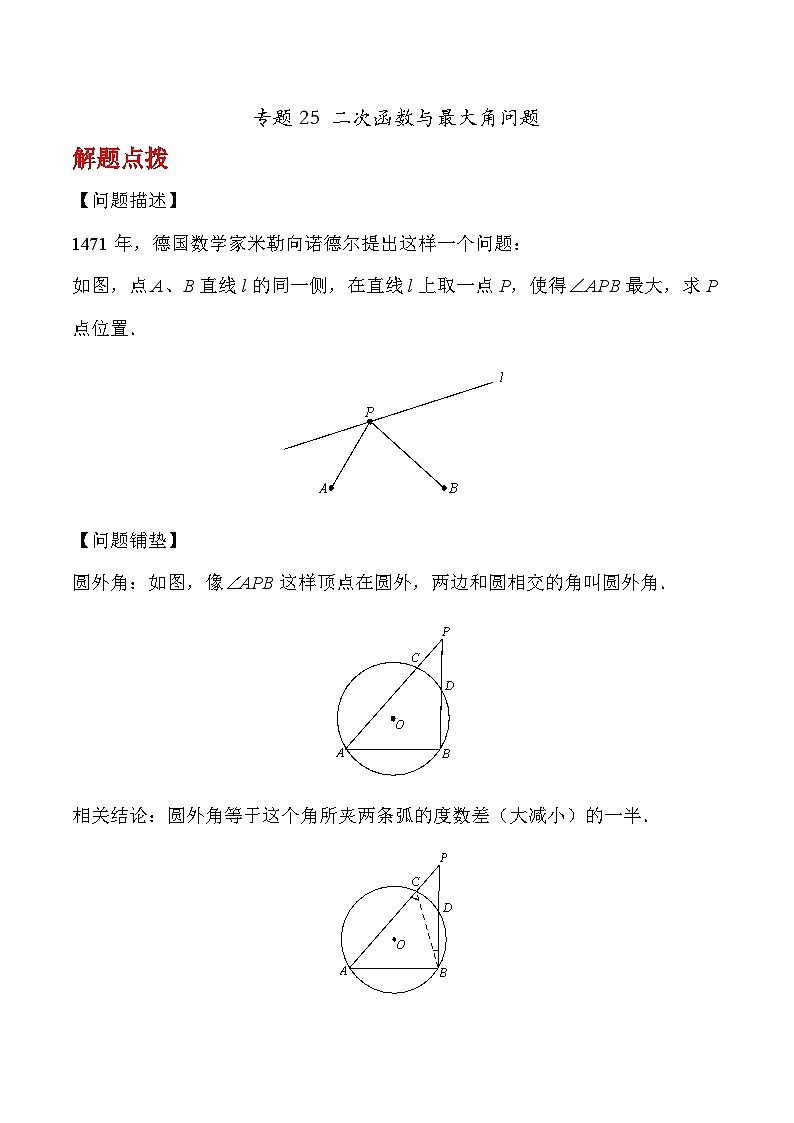
1471年，德国数学家米勒向诺德尔提出这样一个问题：
如图，点A、B直线l的同一侧，在直线l上取一点P，使得∠APB最大，求P点位置．
【问题铺垫】
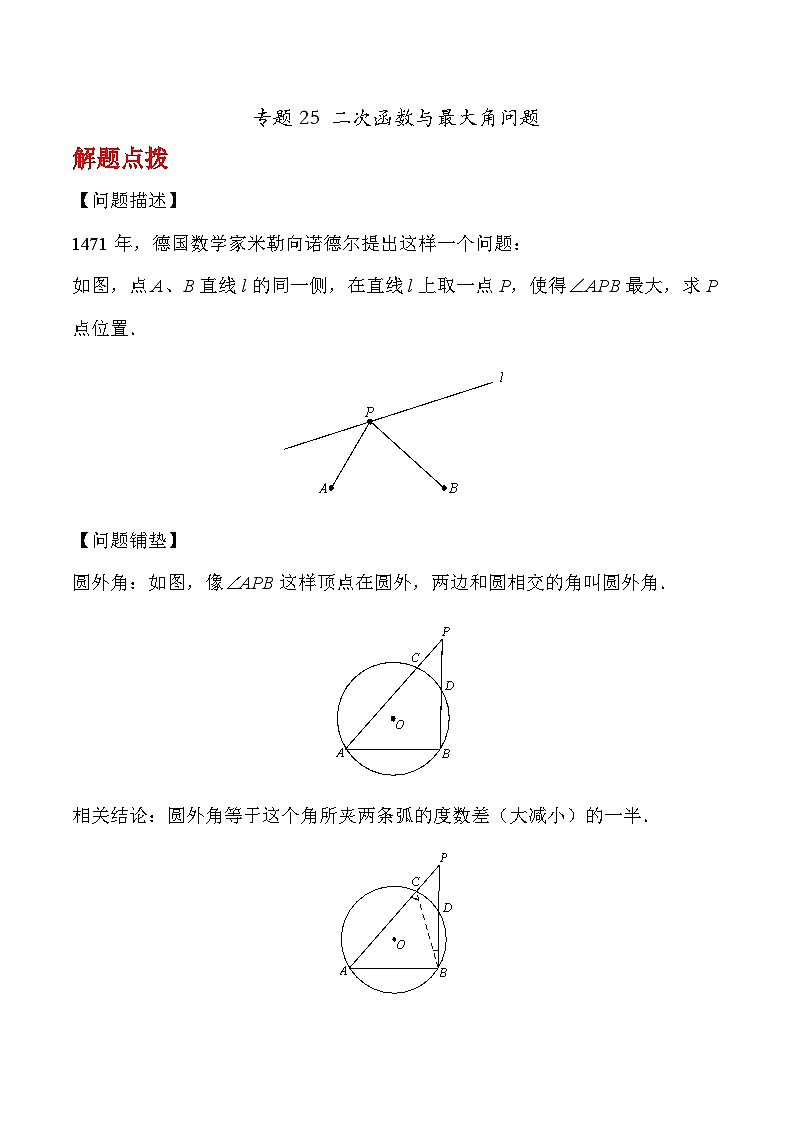
圆外角：如图，像∠APB这样顶点在圆外，两边和圆相交的角叫圆外角．
相关结论：圆外角等于这个角所夹两条弧的度数差（大减小）的一半．
如图，．
换句话说，对同一个圆而言，圆周角>圆外角．
【问题解决】
结论：当点P不与A、B共线时，作△PAB的外接圆，当圆与直线l相切时，∠APB最大．
证明：在直线l上任取一点M（不与点P重合），连接AM、BM，
∠AMB即为圆O的圆外角，
∴∠APB>∠AMB，∠APB最大．
∴当圆与直线l相切时，∠APB最大．
特别地，若点A、B与P分别在一个角的两边，如下图，则有．（切割线定理）
证明：∵∠POA=∠BOP，∠OPA=∠OBP（弦切角定理）
∴△AOP∽△POB，
∴，
∴．
即可通过OA、OB线段长确定OP长，便知P点位置．
直击中考
1．（山东·统考中考真题）如图，顶点为的抛物线与轴交于，两点，与轴交于点，过点作轴交抛物线于另一点，作轴，垂足为点.双曲线经过点，连接，.
(1)求抛物线的表达式；
(2)点，分别是轴，轴上的两点，当以，，，为顶点的四边形周长最小时，求出点，的坐标；
（3）动点P从点O出发,以每秒1个单位长度的速度沿0C方向运动,运动时间为t秒，当t为何值时，∠BPD的度数最大? (请直接写出结果)
【答案】(1)；(2)；；(3)
【分析】（1）先求D的坐标，再代入二次函数解析式解析式求解；
（2）分别作点，关于轴，轴的对称点，，连接交轴，轴于点，.即，F,N，在同同一直线上时，四边形的周长最小，用待定系数法求直线的表达式，再求N,F的坐标；
（3）设P（0，t），作△PBD的外接圆N，当⊙N与y轴相切时，∠BPD的度数最大；
【详解】解：(1)由题意，得点的坐标，.
∵，
∴.
∴点的坐标.
将点，分别代人抛物线，得
解得
∴抛物线的表达式为.
(2)分别作点，关于轴，轴的对称点，，
连接交轴，轴于点，.
由抛物线的表达式可知，顶点的坐标，
∴点的坐标.
设直线为，
∵点的坐标，
∴
解得
∴直线的表达式为.
令，则，解得，
∴点的坐标.
令，则，
∴点的坐标.
（3）设P（0，t），
作△PBD的外接圆N，当⊙N与y轴相切时此时圆心N到BD的距离最小，圆心角∠DNB最大，则，∠BPD的度数最大；
则N（r，t），
∴PN=ND，
∴
∴t2-6t-4r+13=0，
易求BD的中点为
直线BD的解析式为y=-3x+9，
∴BD的中垂线解析式y=
N在中垂线上，
∴t2-18t+21=0，
∴
∴t的值为
【点睛】考核知识点：二次函数的综合运用.数形结合分析问题是关键.
2．如图，已知抛物线y＝ax2﹣2ax﹣3a与x轴交于A，B两点，与y轴交于点C，且顶点的纵坐标为，点D是线段BC的中点，点E、F分别是线段OB，OC上的动点．
（1）求抛物线的解析式；
（2）是否存在点E，F，使得DEF为等边三角形？若存在，请求出点E，F的坐标；若不存在，请说明理由；
（3）当∠BFD的度数最大时，求tan∠OBF的值．
【答案】（1）y＝x²+x+4；（2）存在，DEF为等边三角形时，E（，0），F（0，﹣2）；（3）tan∠OBF＝
【分析】（1）将一般式配方成为顶点式，根据顶点的纵坐标为，列出方程，求出的值，即可求解；
（2）延长至，使，连接，过点作轴交于点，过点作轴交于点，证明，得到，再由中点求出，，则，求出，又由，则，可求，；
（3）过的外接圆，当与轴相切时，切点为，此时最大，设的中点，则，，可证明，由，求出，则，，求出直线的解析式为，设，则，由，得到，再由，可求，则，即可求．
【详解】解：（1）将抛物线化为顶点式：
y＝ax²﹣2ax﹣3a，
＝a（x﹣1）²﹣4a，
∴﹣4a＝，
∴a＝，
∴抛物线的解析式：；
（2）存在，理由如下：
设E（a，0），F（0，b），
令x＝0，则y＝4，
∴C点坐标（0，4），
令y＝0，则，
∴x＝﹣1或3，
∴A（﹣1，0），B（3，0），
∵D为BC的中点，
∴D点坐标（，2），
如图1，延长DE至G，使DE＝EG，连接FG，过点D作DM⊥y轴交于点M，过G点作GN⊥y轴交于点N，
∵DEF是等边三角形，
∴EF＝EG＝DF＝DE，∠DEF＝∠DFE＝60°，
∴∠FEG＝120°，
∴∠EFG＝30°，
∴∠DFG＝90°，
∵∠MFD+∠MDF＝90°，∠MFD+∠NFG＝90°，
∴∠MDF＝∠NFG，
∴FMD∽GNF，
，
，
，
∴，，
，，
，
∵E点是DG的中点，
∴G（2a﹣，﹣2），
∴ON＝2，
，
，
，
，
，
，
，
，，
为等边三角形时，，，；
（3）如图2，过BDF的外接圆M，
当⊙M与y轴相切时，切点为F，此时∠BFD最大，
设的中点，则，，
，
∵OC＝4，BO＝3，
∴CB＝5，
∵∠COB＝∠BHG＝90°，∠CBO＝∠HBG，
∴BOC∽BHG，
，即，
，
，，
设直线GH的解析式为y＝kx+b，
则，
，
，
设M（r，t），则F（0，t），
∵FM＝MB＝r，
∴r2＝t2+（3﹣r）2，
∴t2＝6r﹣9，
，
，
，
，
，
，
，
．
【点睛】本题考查二次函数的综合应用，熟练掌握二次函数的图象及性质，相似三角形的判定及性质，解直角三角形等相关知识以及（2）中倍长线段、构造字型相似，（3）中构造的外接圆与轴相切时最大是解题的关键．
3．（2022·山东日照·日照市新营中学校考一模）如图，已知抛物线经过点和点，与y轴交于点C．
(1)求抛物线的表达式；
(2)若P是直线BC下方的抛物线上一个动点，（不点B，C重合），过点P作y轴的平行线交直线BC于点D，
①求线段PD长度的最大值．
②若为直角三角形，求出P点坐标
(3)点E为y轴上一动点，连接AE，BE，形成，当的度数最大时，求点E的坐标．
【答案】(1)y=x2-4x+3
(2)①；②（1，0）；
(3)或
【分析】（1）用待定系数法求解析式即可；
（2）①根据抛物线解析式设出P点坐标，用待定系数法求出直线BC的解析式，确定D点的坐标，根据二次函数的性质得出PD的最大值即可；
②分情况讨论求出P点的坐标即可；
（3）作△ABE的外接圆，根据圆心在抛物线的对称轴上，且当半径最小时∠AEB有最大值，即外接圆与y轴相切时，求出此时的E点坐标即可．
(1)
解：（1）∵抛物线y=ax2+bx+3经过点A（1，0）和点B（3，0），
∴
解得
∴抛物线的解析式为：y=x2-4x+3；
(2)
①设P（m，m2-4m+3），
由抛物线解析式知，C（0，3），
设直线BC的解析式为y=sx+t，
将点B、C坐标代入得
解得
∴直线BC的解析式为y=-x+3，
∴D（m，-m+3），
∴PD=（-m+3）-（m2-4m+3）
=-m2+3m
=
∴当时，PD有最大值为
(3)
②若△PBD为直角三角形，则存在以下两种情况：
（Ⅰ）如下图，当P点与A点重合时△PBD为直角三角形，
即P（1，0），
（Ⅱ）如下图，当∠DBP=90°时，
∵OB=OC=3，
∴∠DBO=45°，
∴此时△BPD为等腰直角三角形，
由（Ⅰ）知PD=-m2+3m，且BD=BP，
∴-m2+3m=2（3-m），且|-m2-4m+3|=-m+3
此时无解，
∴P点坐标为（1，0）；
（3）如下图，作△ABE的外接圆M，则圆心M在AB的垂直平分线上，即抛物线的对称轴上，
AB长度不变，要使∠AEB最大则当⊙M半径最小时，
即⊙M与y轴相切时，
设E（0，e），则M（2，e），且AM=EM=2，
∴E点的坐标为或
【点睛】本题主要考查二次函数的综合知识，熟练掌握二次函数的性质及分类讨论思想是解题的关键．
4．（2022·山东济宁·统考一模）如图，顶点为M的抛物线y=ax2+bx+3与x轴交于A(﹣1，0)，B两点，与y轴交于点C，过点C作CD⊥y轴交抛物线于另一点D，作DE⊥x轴，垂足为点E，双曲线y=(x＞0)经过点D，连接MD，BD．
（1）求抛物线的表达式；
（2）点N，F分别是x轴，y轴上的两点，当以M，D，N，F为顶点的四边形周长最小时，求出点N，F的坐标；
（3）动点P从点O出发，以每秒1个单位长度的速度沿OC方向运动，运动时间为t秒，当t为何值时，∠BPD的度数最大？
【答案】（1）y=﹣x2+2x+3；（2）N(，0)，F(0，)；（3）t=9﹣2．
【分析】（1）由已知求出D点坐标，将点A（-1，0）和D（2，3）代入y=ax2+bx+3即可；
（2）作M关于y轴的对称点M'，作D关于x轴的对称点D'，连接M'D'与x轴、y轴分别交于点N、F，则以M，D，N，F为顶点的四边形周长最小即为M'D'+MD的长；
（3）设P（0，t），作△PBD的外接圆N，当⊙N与y轴相切时，∠BPD的度数最大；
【详解】解；（1）C(0，3)
∵CD⊥y，
∴D点纵坐标是3．
∵D在y=上，
∴D(2，3)，
将点A(﹣1，0)和D(2，3)代入y=ax2+bx+3，
∴a=﹣1，b=2，
∴y=﹣x2+2x+3；
（2）M(1，4)，B(3，0)，
作M关于y轴的对称点M'，作D关于x轴的对称点D'，连接M'D'与x轴、y轴分别交于点N、F，
则以M，D，N，F为顶点的四边形周长最小即为M'D'+MD的长；
∴M'(﹣1，4)，D'(2，﹣3)，
∴M'D'直线的解析式为y=﹣x+，
∴N(，0)，F(0，)；
（3）设P(0，t)．
∵△PBO和△CDP都是直角三角形，
tan∠CDP=，tan∠PBO=，
令y=tan∠BPD=，
∴yt2+t﹣3yt+6y﹣9=0，
△=﹣15y2+30y+1=0时，
y=(舍)或y=，
∴t=﹣×，
∴t=9﹣2，
∴P(0，9﹣2)．
【点睛】本题考查二次函数的图象及性质；熟练掌握二次函数的图象及性质，利用轴对称求最短距离，学会利用辅助圆解决问题，属于中考压轴题．
5．（2020·浙江宁波·统考模拟预测）已知，如图1，O是坐标原点，抛物线（a≠0）经过A、B、C三点，AB⊥y轴于点A，AB=2，AO=4，OC=5，点D是线段AO上一动点，连接CD、BD．
（1）求出抛物线的解析式；
（2）如图2，抛物线的对称轴分别交BD、CD于点E、F，当△DEF为等腰三角形时，求出点D的坐标；
（3）当∠ BDC的度数最大时，请直接写出OD的长．
【答案】（1）；（2）当△ DEF为等腰三角形时，点D的坐标为（0，）或（0，）或（0，12﹣2）；（3）
【分析】（1）先确定出点A，B，C的坐标，进而用待定系数法即可得出结论．
（2）先判断出要△DEF是等腰三角形，即：△BDH是等腰三角形，设出点D坐标，进而表示出BD，DH，BH，分三种情况建立方程求解即可得出结论．
（3）先判断出当△BDC的外接圆与AO相切时， ∠BDC最大，后利用三角形，勾股定理计算即可．
【详解】（1）∵AB⊥y轴于点A，AB=2，AO=4，OC=5，
∴A（0，4），B（2，4），C（5，0），
∵抛物线a≠0）经过A、B、C三点，
∴
解得,
∴抛物线解析式为．
（2）如图，
过点B作BG⊥OC于G，交CD于H，
∴点H，G的横坐标为2，
∵EF⊥OC，
∴EF∥BH，
∵△DEF是等腰三角形，
∴△BDH是等腰三角形，
设D（0，5m）（0≤m≤），
∵C（5，0），
∴直线CD的解析式为y=﹣mx+5m，
∴H（2，3m），
∴BH=4﹣3m，
∴，，，
当BD=DH时，=，
∴m=（舍）或m=，
∴5m=，
∴D（0，），
当BD=BH时，=，
∴m=，
∴D（0，），
当BH=DH时，=，
∴m=或m=（舍去），
∴D（0，12﹣2），
即：当△DEF为等腰三角形时，点D的坐标为（0，）或（0，）或（0，12﹣2）；
（3）如图，
当△BDC的外接圆与AO相切时， ∠BDC最大，
设外接圆的圆心为E，Q是异于点D的一点，连接QB，QC，交圆于点M，
则∠BDC=∠BMC，根据三角形外角性质，得∠BMC＞∠BQC，故∠BDC＞∠BQC，
∴∠BDC最大，
设OC与圆交于点H，连接DH，DE，
根据切线性质，
∴∠EDO=∠DOC=90°，
作直径HN，连接DN，
∴∠HDN=90°，∠DNH=∠DCH，
∵ED=EH，
∴∠EDH=∠EHD，
∴90°-∠EDH=90°-∠EHD，
∴∠ODH=∠OCD，
∴△ODH∽△OCD，
∴OD：OC=OH：OD，
∴OD：OC=OH：OD，
∴，
设DO=y，OH=x，则HC=5-x，
∴，
∴，
过点E作EF⊥OC，垂足为F，过点B作BG⊥OC，垂足为G，交DE于点P，
根据垂径定理，得HF=FC=，四边形EDOF是矩形，
∴DE=OF=EB=+x=，
根据B（2，4），得AB=DP=OG=2，BG=4，
∴PE=ED-DP==，
∴，
∴，
∴，
∴，
解得，＞4（舍去），
∴，
∴，
故OD=，
∴当∠BDC最大时，OD=．
【点睛】此题是二次函数综合题，主要考查了待定系数法，等腰三角形的性质，垂径定理，勾股定理，矩形的判定和性质，三角形的外接圆，相似三角形的判定和性质，用方程的思想解决问题是解本题的关键．