中考数学二轮培优复习专题04 二次函数中角度问题压轴真题训练（2份，原卷版+解析版）

这是一份中考数学二轮培优复习专题04 二次函数中角度问题压轴真题训练（2份，原卷版+解析版），文件包含中考数学二轮培优复习专题04二次函数中角度问题压轴真题训练原卷版doc、中考数学二轮培优复习专题04二次函数中角度问题压轴真题训练解析版doc等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。
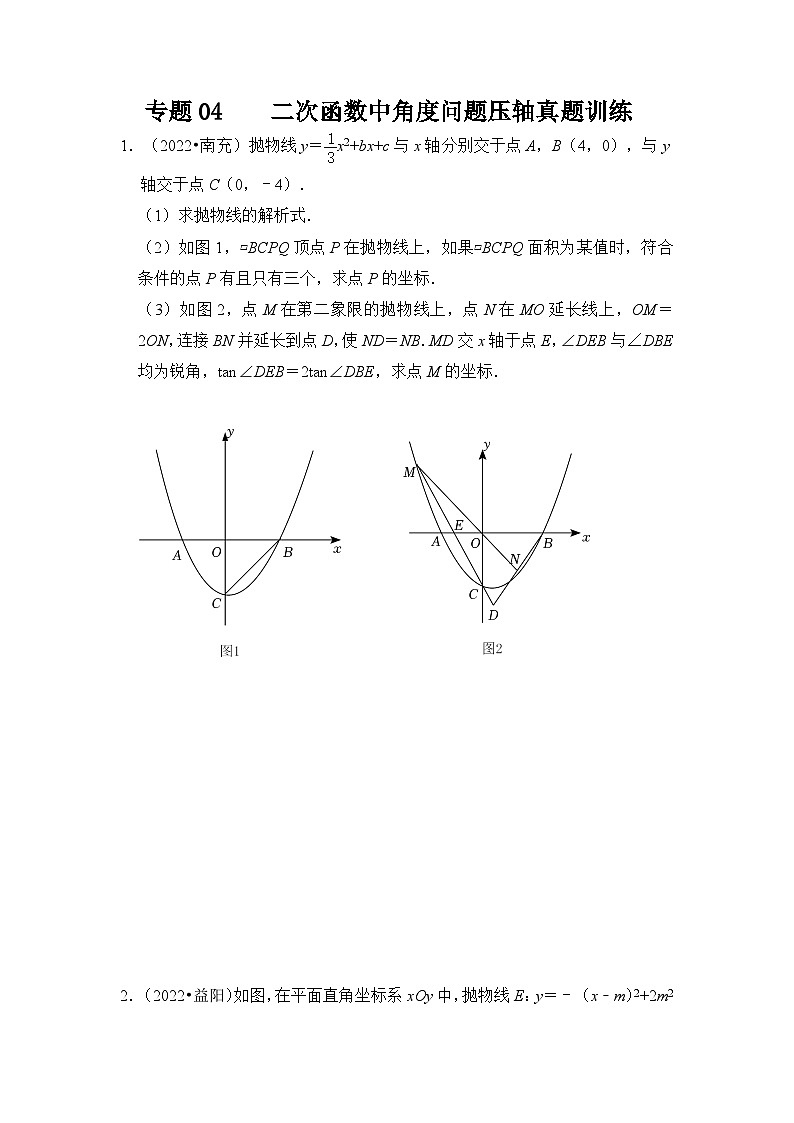
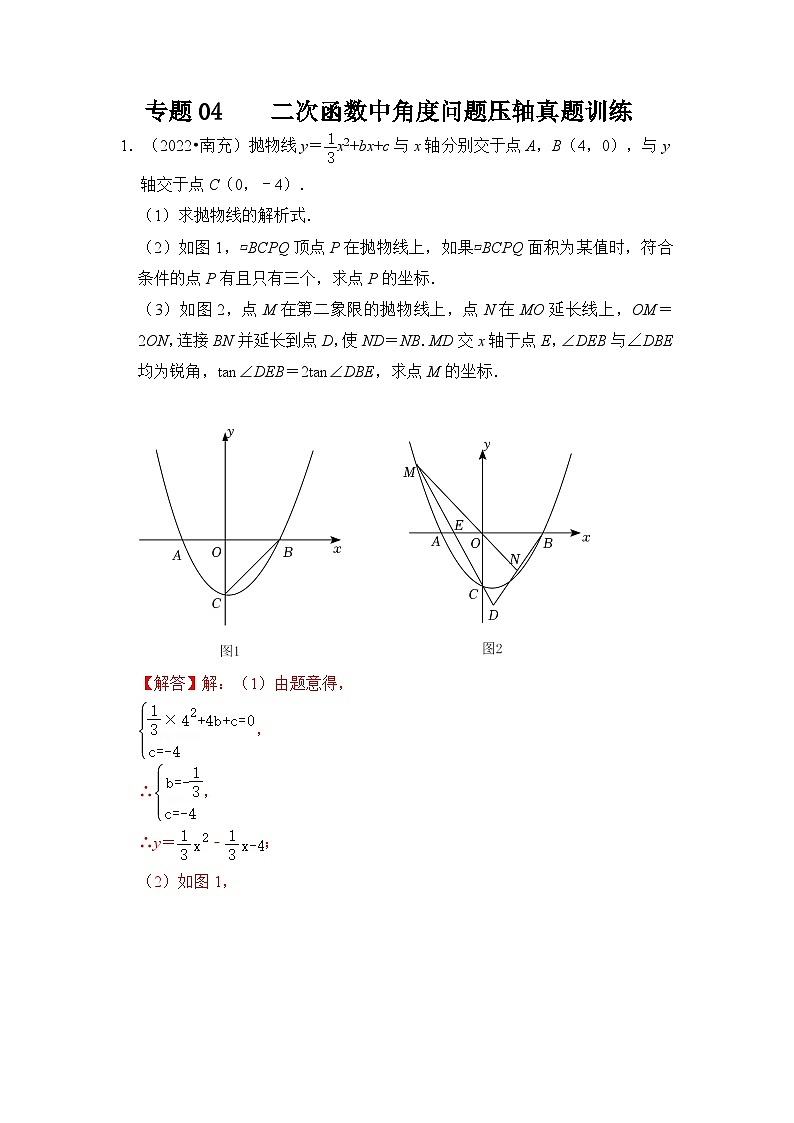
（1）求抛物线的解析式．
（2）如图1，▱BCPQ顶点P在抛物线上，如果▱BCPQ面积为某值时，符合条件的点P有且只有三个，求点P的坐标．
（3）如图2，点M在第二象限的抛物线上，点N在MO延长线上，OM＝2ON，连接BN并延长到点D，使ND＝NB．MD交x轴于点E，∠DEB与∠DBE均为锐角，tan∠DEB＝2tan∠DBE，求点M的坐标．
2．（2022•益阳）如图，在平面直角坐标系xOy中，抛物线E：y＝﹣（x﹣m）2+2m2（m＜0）的顶点P在抛物线F：y＝ax2上，直线x＝t与抛物线E，F分别交于点A，B．
（1）求a的值；
（2）将A，B的纵坐标分别记为yA，yB，设s＝yA﹣yB，若s的最大值为4，则m的值是多少？
（3）Q是x轴的正半轴上一点，且PQ的中点M恰好在抛物线F上．试探究：此时无论m为何负值，在y轴的负半轴上是否存在定点G，使∠PQG总为直角？若存在，请求出点G的坐标；若不存在，请说明理由．
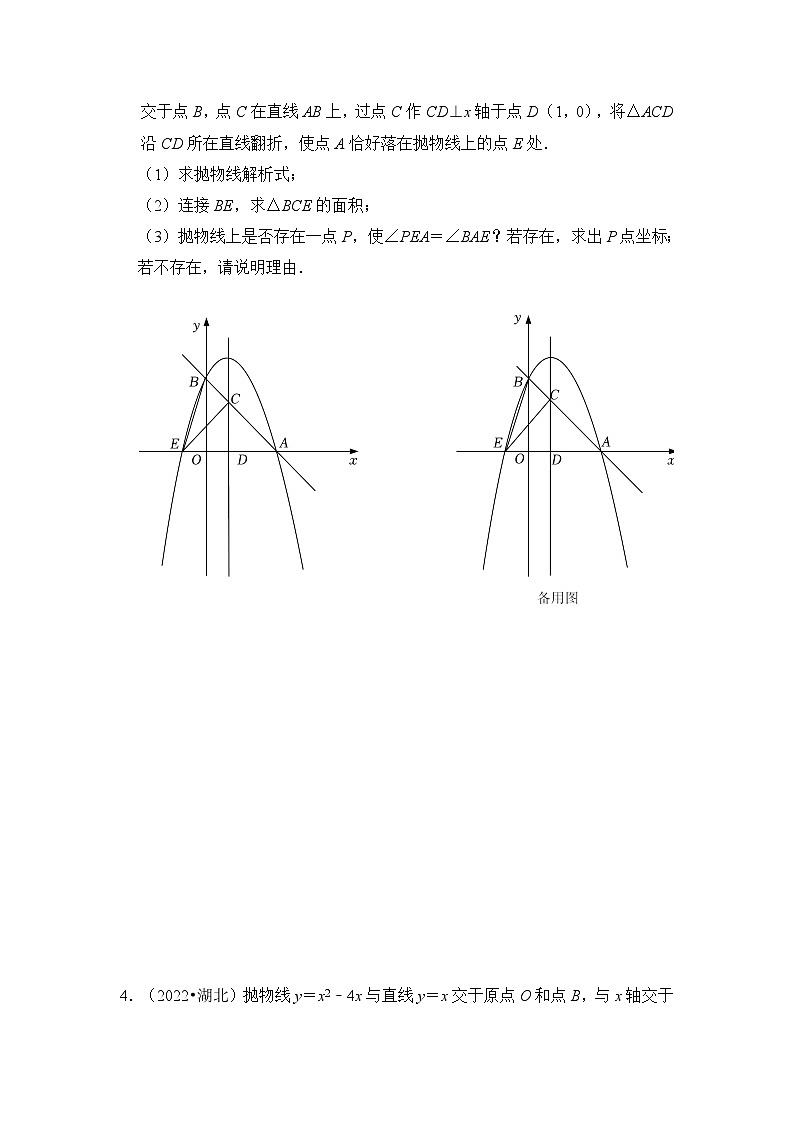
3．（2022•西宁）如图，抛物线y＝ax2+bx+3与x轴交于点A（3，0），与y轴交于点B，点C在直线AB上，过点C作CD⊥x轴于点D（1，0），将△ACD沿CD所在直线翻折，使点A恰好落在抛物线上的点E处．
（1）求抛物线解析式；
（2）连接BE，求△BCE的面积；
（3）抛物线上是否存在一点P，使∠PEA＝∠BAE？若存在，求出P点坐标；若不存在，请说明理由．
4．（2022•湖北）抛物线y＝x2﹣4x与直线y＝x交于原点O和点B，与x轴交于另一点A，顶点为D．
（1）直接写出点B和点D的坐标；
（2）如图1，连接OD，P为x轴上的动点，当tan∠PDO＝时，求点P的坐标；
（3）如图2，M是点B关于抛物线对称轴的对称点，Q是抛物线上的动点，它的横坐标为m（0＜m＜5），连接MQ，BQ，MQ与直线OB交于点E．设△BEQ和△BEM的面积分别为S1和S2，求的最大值．
5．（2022•苏州）如图，二次函数y＝﹣x2+2mx+2m+1（m是常数，且m＞0）的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，顶点为D．其对称轴与线段BC交于点E，与x轴交于点F．连接AC，BD．
（1）求A，B，C三点的坐标（用数字或含m的式子表示），并求∠OBC的度数；
（2）若∠ACO＝∠CBD，求m的值；
（3）若在第四象限内二次函数y＝﹣x2+2mx+2m+1（m是常数，且m＞0）的图象上，始终存在一点P，使得∠ACP＝75°，请结合函数的图象，直接写出m的取值范围．
6．（2022•黄石）如图，抛物线y＝﹣x2+x+4与坐标轴分别交于A，B，C三点，P是第一象限内抛物线上的一点且横坐标为m．
（1）A，B，C三点的坐标为 ， ， ．
（2）连接AP，交线段BC于点D，
①当CP与x轴平行时，求的值；
②当CP与x轴不平行时，求的最大值；
（3）连接CP，是否存在点P，使得∠BCO+2∠PCB＝90°，若存在，求m的值，若不存在，请说明理由．
7．（2022•锦州）如图，抛物线y＝ax2+bx+3交x轴于点A（3，0）和点B（﹣1，0），交y轴于点C．
（1）求抛物线的表达式；
（2）D是直线AC上方抛物线上一动点，连接OD交AC于点N，当的值最大时，求点D的坐标；
（3）P为抛物线上一点，连接CP，过点P作PQ⊥CP交抛物线对称轴于点Q，当tan∠PCQ＝时，请直接写出点P的横坐标．
8．（2022•西宁）如图，抛物线y＝ax2+bx+3与x轴交于点A（3，0），与y轴交于点B，点C在直线AB上，过点C作CD⊥x轴于点D（1，0），将△ACD沿CD所在直线翻折，使点A恰好落在抛物线上的点E处．
（1）求抛物线解析式；
（2）连接BE，求△BCE的面积；
（3）抛物线上是否存在一点P，使∠PEA＝∠BAE？若存在，求出P点坐标；若不存在，请说明理由．
9．（2022•盘锦）如图，抛物线y＝x2+bx+c与x轴交于A，B（4，0）两点（A在B的左侧），与y轴交于点C（0，﹣4）．点P在抛物线上，连接BC，BP．
（1）求抛物线的解析式；
（2）如图1，若点P在第四象限，点D在线段BC上，连接PD并延长交x轴于点E，连接CE，记△DCE的面积为S1，△DBP的面积为S2，当S1＝S2时，求点P的坐标；
（3）如图2，若点P在第二象限，点F为抛物线的顶点，抛物线的对称轴l与线段BC交于点G，当∠PBC+∠CFG＝90°时，求点P的横坐标．
10．（2022•新市区校级三模）综合与探究
如图，抛物线与x轴交于点A（﹣1，0）和点B（4，0），与y轴交于点C，连接BC．
（1）求抛物线的表达式及点C的坐标；
（2）点P是抛物线对称轴上一点，点Q为平面内一点，当以点B、C、P、Q为顶点的四边形是以BC为边的矩形时，请直接写出点P的坐标；
（3）点D是第四象限内抛物线上一动点，当∠BCD＝2∠ABC时，求点D的坐标．