中考数学二轮培优复习专题30 中考命题核心元素全等三角形的基本模型的应用（2份，原卷版+解析版）

这是一份中考数学二轮培优复习专题30 中考命题核心元素全等三角形的基本模型的应用（2份，原卷版+解析版），文件包含中考数学二轮培优复习专题30中考命题核心元素全等三角形的基本模型的应用原卷版doc、中考数学二轮培优复习专题30中考命题核心元素全等三角形的基本模型的应用解析版doc等2份试卷配套教学资源，其中试卷共46页， 欢迎下载使用。
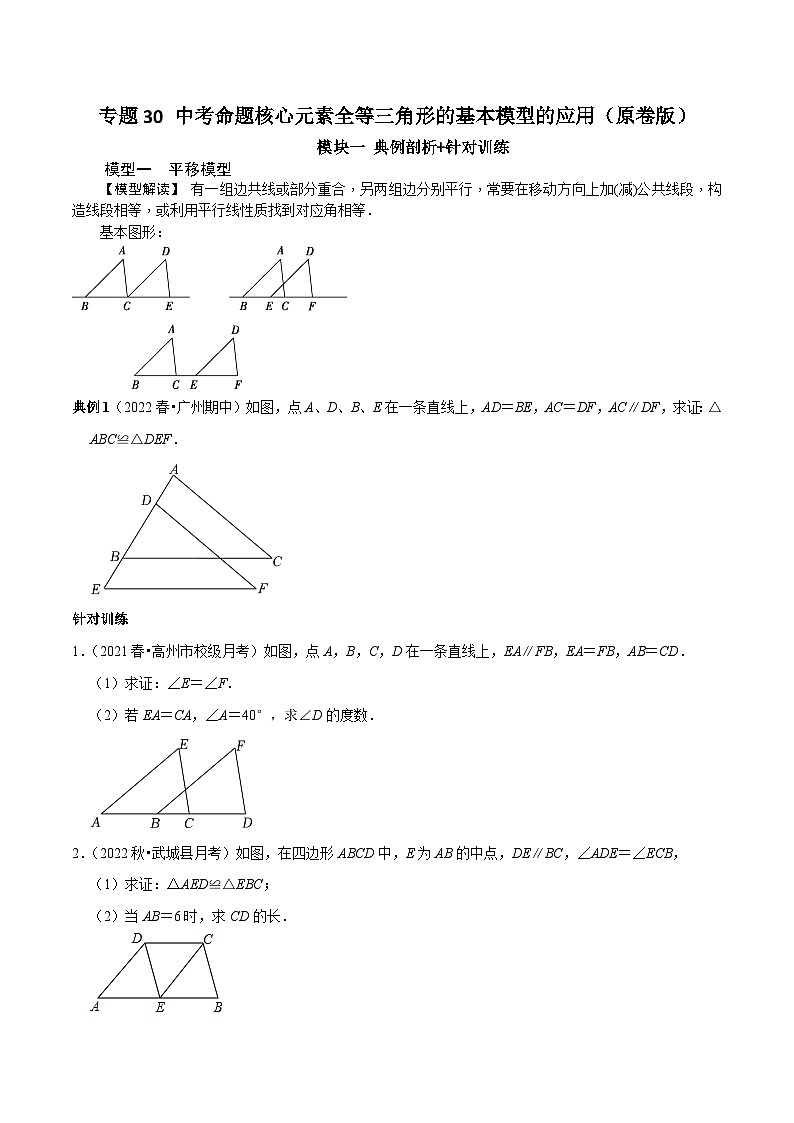
模型一 平移模型
【模型解读】 有一组边共线或部分重合，另两组边分别平行，常要在移动方向上加(减)公共线段，构造线段相等，或利用平行线性质找到对应角相等．
基本图形：
典例1（2022春•广州期中）如图，点A、D、B、E在一条直线上，AD＝BE，AC＝DF，AC∥DF，求证：△ABC≌△DEF．
针对训练
1．（2021春•高州市校级月考）如图，点A，B，C，D在一条直线上，EA∥FB，EA＝FB，AB＝CD．
（1）求证：∠E＝∠F．
（2）若EA＝CA，∠A＝40°，求∠D的度数．
2．（2022秋•武城县月考）如图，在四边形ABCD中，E为AB的中点，DE∥BC，∠ADE＝∠ECB，
（1）求证：△AED≌△EBC；
（2）当AB＝6时，求CD的长．
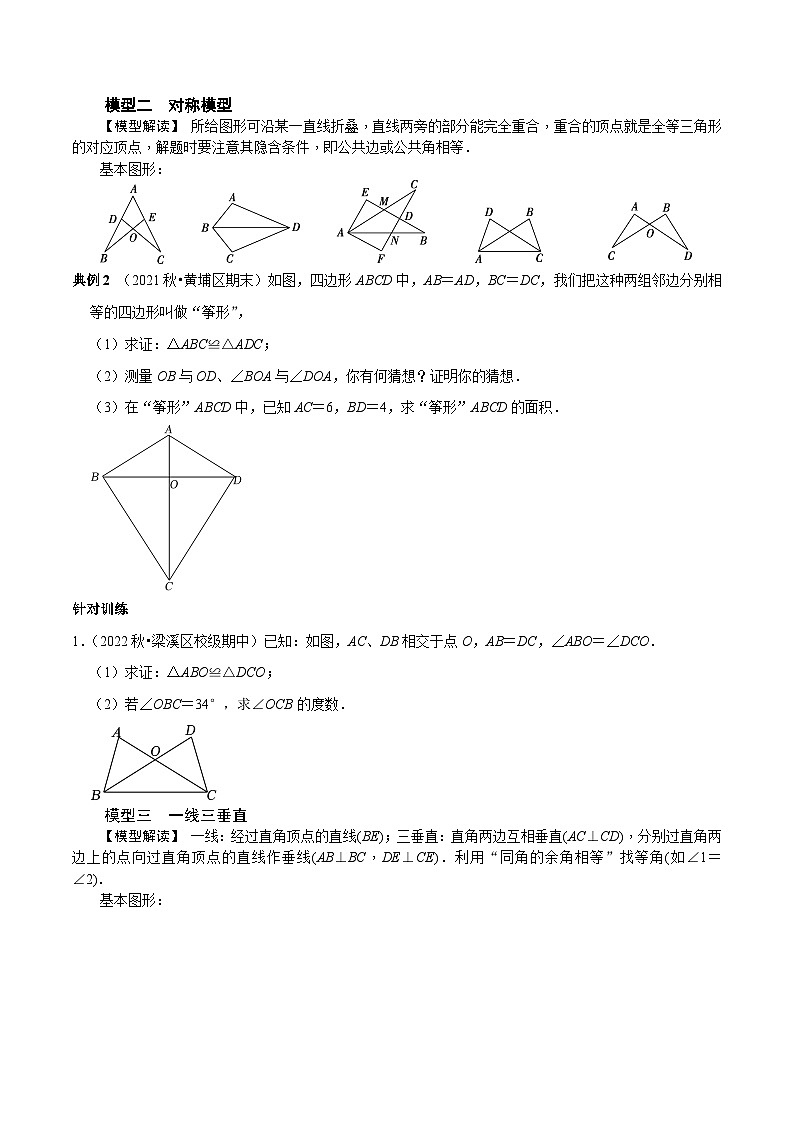
模型二 对称模型
【模型解读】 所给图形可沿某一直线折叠，直线两旁的部分能完全重合，重合的顶点就是全等三角形的对应顶点，解题时要注意其隐含条件，即公共边或公共角相等．
基本图形：

典例2 （2021秋•黄埔区期末）如图，四边形ABCD中，AB＝AD，BC＝DC，我们把这种两组邻边分别相等的四边形叫做“筝形”，
（1）求证：△ABC≌△ADC；
（2）测量OB与OD、∠BOA与∠DOA，你有何猜想？证明你的猜想．
（3）在“筝形”ABCD中，已知AC＝6，BD＝4，求“筝形”ABCD的面积．
针对训练
1．（2022秋•梁溪区校级期中）已知：如图，AC、DB相交于点O，AB＝DC，∠ABO＝∠DCO．
（1）求证：△ABO≌△DCO；
（2）若∠OBC＝34°，求∠OCB的度数．
模型三 一线三垂直
【模型解读】 一线：经过直角顶点的直线(BE)；三垂直：直角两边互相垂直(AC⊥CD)，分别过直角两边上的点向过直角顶点的直线作垂线(AB⊥BC，DE⊥CE)．利用“同角的余角相等”找等角(如∠1＝∠2)．
基本图形：
典例3（2022秋•汝城县期末）如图，在正方形ABCD中，点E、F分别在BC、CD边上运动，且始终保持BE＝CF．连接AE、BF．
（1）求证：△ABE≌△BCF；
（2）求证：AE⊥BF；
（3）若AB＝10cm，红蚂蚁P以2.6厘米/秒的爬行速度从点B出发，黑蚂蚁Q以3厘米/秒的爬行速度从点C同时出发，都逆时针沿正方形ABCD的边爬行，求经过多长时间，两只蚂蚁第一次在正方形ABCD的哪条边上相遇？
针对训练
1．（2020•苏州）问题1：如图①，在四边形ABCD中，∠B＝∠C＝90°，P是BC上一点，PA＝PD，∠APD＝90°．求证：AB+CD＝BC．
问题2：如图②，在四边形ABCD中，∠B＝∠C＝45°，P是BC上一点，PA＝PD，∠APD＝90°．求的值．
2．（2022•定远县模拟）如图，已知：Rt△ABC中，∠BAC＝90°，AB＝AC，点D是BC的中点，点P是BC边上的一个动点．
（1）如图1，若点P与点D重合，连接AP，则AP与BC的位置关系是 ；
（2）如图2，若点P在线段BD上，过点B作BE⊥AP于点E，过点C作CF⊥AP于点F，则CF，BE和EF这三条线段之间的数量关系是 ；
（3）如图3，在（2）的条件下，若BE的延长线交直线AD于点M，求证：CP＝AM；
（4）如图4，已知BC＝4，若点P从点B出发沿着BC向点C运动，过点B作BE⊥AP于点E，过点C作CF⊥AP于点F，设线段BE的长度为d1，线段CF的长度为d2，试求出点P在运动的过程中d1+d2的最大值．
模型四 旋转模型
【模型解读】 可看成将三角形绕着公共顶点旋转一定角度，旋转后的图形与原图形之间存在两种情况：
(1)无重叠：两个三角形有公共顶点，无重叠部分一般有一对相等的角隐含在平行线、对顶角中．

(2)有重叠：两个三角形含有一部分公共角，运用角的和差得到等角．
典例4（2021秋•长丰县月考）如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连接BD，CE，BD与CE交于点O，BD与AC交于点F．
（1）求证：BD＝CE．
（2）若∠BAC＝48°，求∠COD的度数．
（3）若G为CE上一点，GE＝OD，AG＝OC，且AG∥BD，求证：BD⊥AC．
针对训练
1．（2022春•驻马店期末）如图，在△ADC中，DB是高，点E是DB上一点，AB＝DB，EB＝CB，M，
N分别是AE，CD上的点，且AM＝DN．
（1）试说明：△ABE≌△DBC；
（2）探索BM和BN的位置关系和数量关系，并说明理由．
2．（2021•南通一模）如图，四边形ABCD是正方形，点E是平面内异于点A的任意一点，以线段AE为边作正方形AEFG，连接EB，
GD．
（1）如图1，求证EB＝GD；
（2）如图2，若点E在线段DG上，AB＝5，AG＝3，求BE的长．
模块二 2023中考押题预测
1．（2021秋•西山区期末）如图，AB＝DE，AC＝DF，BE＝CF，求证：△ABC≌△DEF．
2．（2020秋•开福区月考）如图，在△ABC中，点D是BC上一点，且AD＝AB，AE∥BC，∠BAD＝∠CAE，连接DE交AC于点F．
（1）若∠C＝40°，求∠B的度数；
（2）若AD平分∠BDE，求证：AE＝AC．
3．（2022秋•南昌期末）如图，在△ABC和△DBC中，∠ACB＝∠DBC＝90°，点E是BC的中点，DE⊥AB于点F，且AB＝DE．
（1）求证：△ACB≌△EBD；
（2）若DB＝12，求AC的长．
4．如图（1）矩形ABCD中，AB＝2，BC＝5，BP＝1，∠MPN＝90°将∠MPN绕点P从PB处开始按顺时针方向旋转，PM交AB（或AD）于点E，PN交边AD（或CD）于点F，当PN旋转至PC处时，∠MPN的旋转随即停止
（1）特殊情形：如图（2），发现当PM过点A时，PN也恰好过点D，此时，△ABP △PCD（填：“≌”或“～”）；
（2）类比探究：如图（3）在旋转过程中，的值是否为定值？若是，请求出该定值；若不是，请说明理由；
（3）拓展延伸：设AE＝t，当△EPF面积为4.2时，直接写出所对应的t的值．
5．如图，在△ABC中，∠ACB＝90°，AC＝BC，过C点任作一条直线PQ，过A作AM⊥PQ于M，过B作BN⊥PQ于N．
（1）如图1，当直线MN在△ABC的外部时，MN，AM，BN有什么关系呢？为什么？
（2）如图2，当直线MN经过△ABC内部时，（1）中的结论是否仍然成立？若成立，请说明理由；若不成立，请指出MN与AM，BN之间的数量关系并说明理由
.
6．（2021•泗洪县三模）如图，E、F是正方形ABCD的对角线AC上的两点，BE∥DF．求证：AE＝CF．
7．（2021秋•迁安市期末）小明将两个大小不同的含45°角的直角三角板如图1所示放置在同一平面内．从图1中抽象出一个几何图形（如图2），B、C、E三点在同一条直线上，连结DC．猜想线段CD与BE的数量关系和位置关系，并证明．
8．（2020•渝中区二模）如图，在△ABC中，∠ACB＝90°，AC＝BC，CD⊥AB于点D，E为线段CD上一点（不含端点），连接AE，设F为AE的中点，作CG⊥CF交直线AB于点G．
（1）猜想：线段AG、BC、EC之间有何等量关系？并加以证明；
（2）如果将题设中的条件“E为线段CD上一点（不含端点）”改变为“E为直线CD上任意一点”，试探究发现线段AG、BC、EC之间有怎样的等量关系，请直接写出你的结论，不用证明．
9．（2020秋•盐都区期末）已知：如图，AC与BD相交于点O，AC⊥BC，AD⊥BD，垂足分别为点C、D，且AC＝BD．求证：OA＝OB．
10．（2021•南通一模）如图，四边形ABCD是正方形，点E是平面内异于点A的任意一点，以线段AE为边作正方形AEFG，连接EB，GD．
（1）如图1，求证EB＝GD；
（2）如图2，若点E在线段DG上，AB＝5，AG＝3，求BE的长．
11．（2021春•沙坪坝区校级月考）△ABC是直角三角形，∠ACB＝90°，点D在直线BC上，过B作BA的垂线交AD的延长线于点E．
（1）如图1，若∠ABC＝30°，tan∠EAB，BC，求AE的长；
（2）如图2，点F是CA延长线上的一点，连接FE交BC于点M，若CF＝CB，且∠CAE＝∠FBA，求证AF＝2CM；
（3）如图3，AC＝1，BC＝2，点M为AE的中点，连接BM，CM，当|BM﹣CM|最大时，直接写出的值．