中考数学二轮培优题型训练压轴题18以圆为背景的几何类比探究压轴问题（2份，原卷版+解析版）

这是一份中考数学二轮培优题型训练压轴题18以圆为背景的几何类比探究压轴问题（2份，原卷版+解析版），文件包含中考数学二轮培优题型训练压轴题18以圆为背景的几何类比探究压轴问题原卷版doc、中考数学二轮培优题型训练压轴题18以圆为背景的几何类比探究压轴问题解析版doc等2份试卷配套教学资源，其中试卷共85页， 欢迎下载使用。
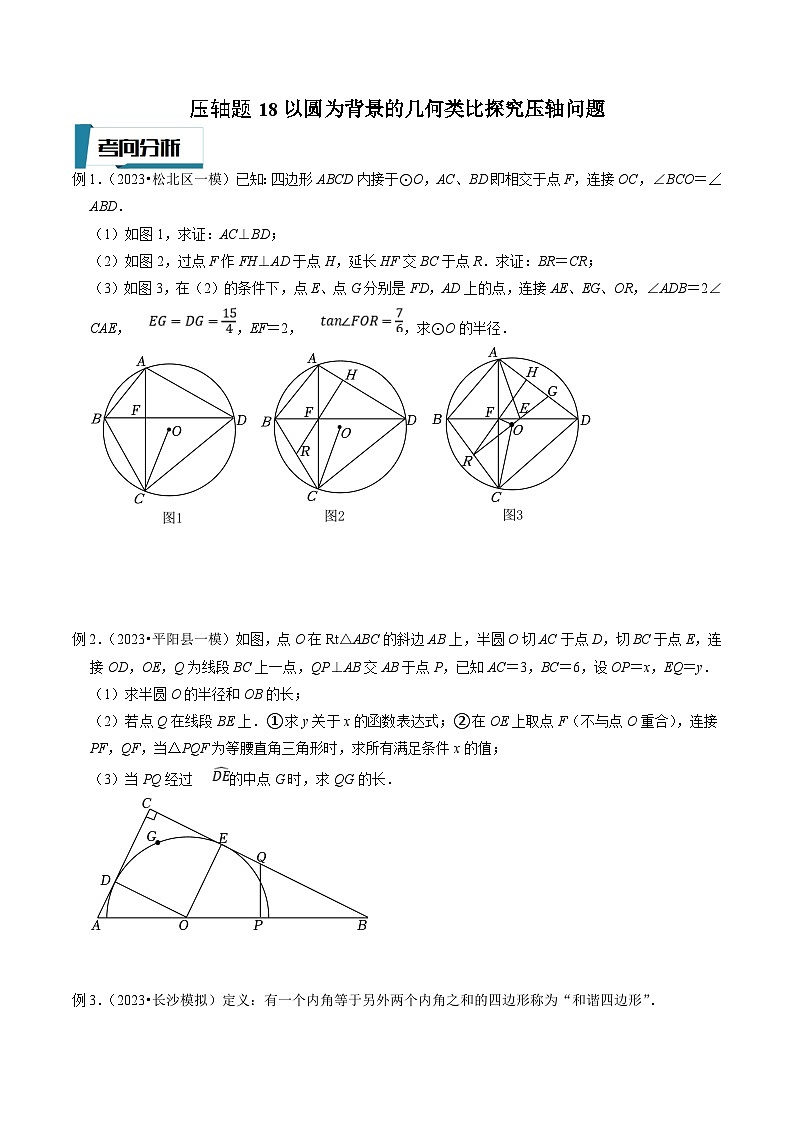
例1．（2023•松北区一模）已知：四边形ABCD内接于⊙O，AC、BD即相交于点F，连接OC，∠BCO＝∠ABD．
（1）如图1，求证：AC⊥BD；
（2）如图2，过点F作FH⊥AD于点H，延长HF交BC于点R．求证：BR＝CR；
（3）如图3，在（2）的条件下，点E、点G分别是FD，AD上的点，连接AE、EG、OR，∠ADB＝2∠CAE，，EF＝2，，求⊙O的半径．
【分析】（1）延长CO交圆于点S，连接BS，根据圆周角性质及题中等量条件得出结论即可；
（2）根据互余关系得出∠AFH＝∠ADB＝α，根据等腰三角形的性质推出RF＝RC，RB＝RF，等量代换得出RB＝RC即可；
（3）在FB上截取FM＝FE，连接AM，证DA＝DM，设DE＝a，利用勾股定理求出a的值，作AN⊥GE于N，作FT⊥BC于T，设TF＝4b，BT＝3b，设TR＝x，利用勾股定理求出x的值，过点F，作FW⊥OR于W，设FW＝7m，则RW＝24m，利用勾股定理求出m的值，最后利用勾股定理求出半径即可．
【解答】（1）证明：延长CO交圆于点S，连接BS，
∴∠A＝∠S，
∵CM为直径，
∴∠CBD＝90°，
在Rt△BSC中，∠BCO+∠S＝90°，
又∵∠ABD＝∠BCO，
∴∠ABD+∠A＝90°，
∴∠BFA＝90°，
∴AC⊥BD；
（2）证明：由（1）得，∠ADB＝∠ACB＝α，
∵FH⊥AD，
∴∠AFH+∠FAD＝90°，∠ADB+∠FAD＝90°，
即∠AFH＝∠ADB＝α，
∴∠RFC＝∠AFH＝α，
∴∠RFC＝∠RCF，
∴RF＝RC，
∵FB⊥CF，
∴∠BFR＝90°﹣α，∠CBF＝90°﹣α，
∴∠BFR＝∠CBF，
∴RB＝RF，
∴RB＝RC，
即BR＝CR；
（3）解：∵∠ADB＝2∠CAE，
∴设∠EAF＝β，则∠ADB＝2β，
又∵AC⊥BD，
∴∠AFD＝90°，
∴在Rt△AFD中，∠FAD＝90°﹣∠ADF＝90°﹣2β，
又∵RH⊥AD，
∴∠AHF＝90°，
∴在Rt△AFH中，∠AFH＝90°﹣∠HAF＝2β，
同理在Rt△AFE中，∠AEF＝90°﹣∠EAF＝90°﹣β，
在FB上截取FM＝FE，连接AM，
∵AF⊥BD，
∴AM＝AE，
∴∠AMD＝∠AEF＝90°﹣β，
∴∠DAM＝180°﹣∠ADM﹣∠AMD＝90°﹣β，
∴∠AMD＝∠AMD，
∴DA＝DM，
设DE＝a，
∴DM＝DA＝a+4，，
又∵EG＝DG，
∴∠GED＝∠GDE＝2β，
∴∠AEG＝180°﹣∠AEB﹣∠GED＝90°﹣β，
∴EA平分∠FEG，
作AN⊥GE于N，
∴AF＝AN，EF＝EN＝2，，
由勾股定理知，AF2＝AD2﹣DF2，AN2＝AG2﹣GN2，
∴AG2﹣GN2＝AD2﹣DF2，
∴，
∴a＝6，
∴AD＝10，AF＝6，DF＝a+2＝8，
∴，
∴，
在Rt△BCF中，，
又由（2）得CB＝2CR，
∴即，
∵∠RCO＝∠ABD＝∠FCD，
∴tan∠RCO＝tan∠FCD，
即在Rt△ROC、Rt△CFD中，，
∴，
又∵DF＝8，
∴OR＝5，
作FT⊥BC于T，
∴∠FTR＝90°，
又∵，
设TF＝4b，BT＝3b，TR＝x，
∵FR＝BR，
∴FR＝x+3b，
∵FR2＝FT2+TR2，
∴（x+3b）2＝（4b）2+x2，
∴xb，
∴tan∠TFR，
∵∠FTR＝∠ORC＝90°，
∴FT∥OR，
∴∠TFR＝∠FRO，
∴tan∠FRO，
又∵tan∠FOR，
过点F，作FW⊥OR于W，
设FW＝7m，则RW＝24m，
∴RF25m，则OW＝6m，
∴OR＝RW+OW＝24m+6m＝30m＝5，
∴m，
∴FR＝25mRC，
∵OC2＝RC2+ER2，
∴r＝OC，
即⊙O的半径为．
【点评】本题主要考查圆的综合题型，熟练掌握勾股定理，圆周角的性质，三角函数等知识是解题的关键．
例2．（2023•平阳县一模）如图，点O在Rt△ABC的斜边AB上，半圆O切AC于点D，切BC于点E，连接OD，OE，Q为线段BC上一点，QP⊥AB交AB于点P，已知AC＝3，BC＝6，设OP＝x，EQ＝y．
（1）求半圆O的半径和OB的长；
（2）若点Q在线段BE上．①求y关于x的函数表达式；②在OE上取点F（不与点O重合），连接PF，QF，当△PQF为等腰直角三角形时，求所有满足条件x的值；
（3）当PQ经过的中点G时，求QG的长．
【分析】（1）利用圆的切线的性质，直角三角形的性质和正方形的判定与性质得到矩形OECD为正方形，再利用相似三角形的判定与性质和勾股定理解答即可得出结论；
（2）①利用直角三角形的边角关系定理列出关于x，y的等式，整理即可得出结论；
②利用分类讨论的思想方法，分两种情形同理解答：当∠FQP为90°时，利用直角三角形的边角关系定理分别表示出PQ和FQ，利用PQ＝FQ得到关于x的方程，解方程即可；当∠PFQ＝90°时，过F点作FM⊥OP交OP于M点，求得OM，FM，利用直角三角形的边角关系定理列出关于x的方程，解方程即可；
（3）过点G作GH⊥BC于点H，GN⊥OE于点N，连接OG，利用矩形的判定与性质和直角三角形的边角关系定理，设QH＝a，则GH＝2a，QGa，利用圆心角，弧，弦之间的关系定理和等腰直角三角形的判定与性质列出关于a的方程，解方程即可得出结论．
【解答】解：（1）∵半圆O切AC于点D，切BC于点E，
∴OD⊥AC，OE⊥BC，
∴∠ODC＝∠OEC＝∠DCE＝90°，
∴四边形OECD为矩形，
∵OD＝OE，
∴矩形OECD为正方形，
∴OD＝CD＝CE＝OE，
∴OD∥BC，OE∥AC，
∴∠AOD＝∠B，
∴△AOD∽△ABC，
∴，
∴OD＝2AD，
∴CD＝2AD，
∴CD+AD＝AC＝3，
∴2AD+AD＝3
∴AD＝1，
∴BD＝2，
∴OD＝2，
∴AO，
∵AB3，
∴BO＝AB﹣AO＝2．
（2）①∵OP＝x，
∴BP＝BO﹣OP＝2x，
∵EQ＝y，
∴BQ＝BC﹣CE﹣EQ＝6﹣2﹣y＝4﹣y，
∵cs∠B，
∵PQ⊥AB，
∴cs∠B，
∴，
∴yx﹣1；
②当∠FQP为90°时，如图，
PQ＝tan∠B•BP•BP•（2x）x，
∵FQ⊥PQ，AB⊥PQ，
∴FQ∥AB，
∴∠FQE＝∠B，
∵∠FEQ＝90°，
∴FQ，
∵FQ＝PQ，
∴x，
∴x，
如图，当∠PFQ＝90°时，
过F点作FM⊥OP交OP于M点，
∵FQ＝FP，∠PFQ＝90°，
∴FQ＝FPPQ，∠FPQ＝∠FQP＝45°，
∴∠FPM＝45°，
∴FM＝PMFPPQ（x）x，
∴OM＝OP﹣PM＝OPPQ＝x（x），
∵FM⊥OB，
∴∠FOM+∠OFM＝90°，
∵OE⊥BC，
∴∠FOM+∠B＝90°，
∴∠OFM＝∠B．
∴tan∠OFM＝tan∠B．
∵tan∠OFM，
∴，
解：x．
综上，满足条件x的值为或；
（3）过点G作GH⊥BC于点H，GN⊥OE于点N，连接OG，如图，
∵OE⊥BC，GH⊥BC，GN⊥OE，
∴四边形HGNE为矩形，
∴GH＝EN，HE＝GN．
∵GH⊥BC，
∴∠QGH+∠GQH＝90°，
∵QP⊥AB，
∴∠B+∠GQH＝90°，
∴∠QGH＝∠B，
∴tan∠QGH＝tan∠B．
∵tan∠QGH，
∴，
设QH＝a，则GH＝2a，QGa．
∴EN＝GH＝2a，
∴ON＝OE﹣EN＝2﹣2a．
∵G为的中点，
∴∠GOE＝∠GOD∠DOE＝45°，
∴△OGN为等腰直角三角形，
∴ONOG，
∴2﹣2a2，
∴a，
∴QGa．
【点评】本题主要考查了圆的有关性质，圆周角定理，正方形的判定与性质，相似三角形的判定与性质，直角三角形的性质，直角三角形的边角关系定理，等腰直角三角形的判定与性质，勾股定理，圆的切线的性质，恰当的条件辅助线构造等腰直角三角形是解题的关键．
例3．（2023•长沙模拟）定义：有一个内角等于另外两个内角之和的四边形称为“和谐四边形”．
（1）已知∠A＝100°，∠B＝60°，∠C＝α，请直接写出一个α的值 150°或40°或160°或130°（写一个即可） ，使四边形ABCD为“和谐四边形”．
（2）如图1，在△ABC中，D，E分别是边AB，AC上的点，AE＝DE．求证：四边形DBCE为“和谐四边形”．
（3）在（2）的条件下，如图2，过D，E，C三点作⊙O，与边AB交于点F，与边BC交于点G，连接FG，EG是⊙O的直径．
①求证：BF＝FC；
②若AE＝1，，∠BGF﹣∠B＝45°，求“和谐四边形”DBCE的面积．
【分析】（1）先根据四边形的内角和为360°表示∠D的度数，根据“和谐四边形”的定义分8种情况列方程可得结论；
（2）根据条件证明∠BDE＝∠B+∠C，由“和谐四边形”的定义可得结论；
（3）①根据圆周角定理及直角三角形的性质推出，∠ACF+∠BCF＝90°，∠A+∠B＝90°，根据圆内接四边形的性质和等腰三角形的性质推出∠ADE＝∠FGE，∠ADE＝∠A，进而得出∠A＝∠ACF，根据等式的性质求解即可；
②如图3，作辅助线，构建相似三角形，证明△AHE∽△ACB，根据勾股定理和相似三角形的性质求解即可．
【解答】（1）解：∵∠A＝100°，∠B＝60°，∠C＝α，
∴∠D＝360°﹣100°﹣60°﹣α＝200°﹣α，
若∠A＝∠B+∠D，则100°＝50°+（200°﹣α），解得：α＝150°，
若∠A＝∠C+∠B，则100°＝α+60°，解得：α＝40°，
若∠A＝∠C+∠D，则100°＝α+（200°﹣α），无解，
若∠B＝∠D+∠C，则60°＝200°﹣α+α，无解，
若∠C＝∠B+∠A，则α＝160°，
若∠C＝∠B+∠D，则α＝60°+（200°﹣α），α＝130°，
综上，α的值是150°或40°或160°或130°（写一个即可），
故答案为：150°或40°或160°或130°（写一个即可）；
（2）证明：设∠A＝x，∠C＝y，则∠B＝180°﹣x﹣y，
∵AE＝DE，
∴∠ADE＝∠A＝x，
∴∠BDE＝180°﹣x，
在四边形DBCE中，∠BDE＝∠B+∠C，
∴四边形DBCE为“和谐四边形”；
（3）①证明：∵EG是⊙O的直径，
∴∠GCE＝90°，
∴∠ACF+∠BCF＝90°，∠A+∠B＝90°，
∵AE＝DE，
∴∠ADE＝∠A，
∵D、F、G、E四点都在⊙O上，
∴∠ADE＝∠FGE，
∴∠FGE＝∠A，
∵∠FGE＝∠ACF，
∴∠A＝∠ACF，
∴∠B＝∠BCF，
∴BF＝CF；
②解：连接DE、DG、FG，过E作EH⊥AB于H，连接DG，
∵BF＝CF，
∴∠B＝∠BCF＝∠BDG，
∴BG＝DG，
∵EG是⊙O的直径，
∴∠GDE＝90°，
∵DE＝AE＝1，EG＝5，
∴DG7＝BG，
∵∠BGF﹣∠B＝45°，∠BGF﹣∠BCF＝∠CFG，
∴∠CFG＝∠CEG＝45°，
∴△ECG是等腰直角三角形，
∴CE＝CGEG＝5，
∴BC＝7+5＝12，AC＝5+1＝6，
∴AB6，
∵∠AHE＝∠ACB＝90°，∠A＝∠A，
∴△AHE∽△ACB，
∴，，
∵，
∴AH，，
∴EH，
∴S△AHEAH•EH，
∴S△ACB36，
∵DE＝AE，EH⊥AD，
∴S△ADE＝2S△AHE，
∴“和谐四边形”DBCE的面积＝S△ACB﹣S△ADE＝36．
【点评】本题是圆的综合题，考查圆周角定理，圆内接四边形的性质，相似三角形的性质和判定，新定义：“和谐四边形”的理解和运用，勾股定理等知识，解题的关键是学会理解新定义，正确作辅助线解决问题，属于中考压轴题．
例4．（2023•海淀区校级模拟）在平面直角坐标系xOy中，已知点M（a，b），N．
对于点P给出如下定义：将点P向右（a≥0）或向左（a＜0）平移|a|个单位长度，再向上（b≥0）或向下（b＜0）平移|b|个单位长度，得到点P'，点P'关于点N的对称点为P″，NP″中点记为Q，称点Q为点P的“对应点”．
（1）如图，点M（1，1），点N在线段OM的延长线上，若点P（﹣3，0），点Q为点P的“对应点”．
①在图1中画出点Q；
②连接PQ，交线段ON于点T．求证：；
（2）⊙O的半径为2，M是⊙O上一点，点N在线段OM上，且ON＝t（1＜t＜2），若P为⊙O外一点，点Q为点P的“对应点”，连接PQ．当点M在⊙O上运动时，直接写出PQ长的最大值与最小值的差（用含t的式子表示）．
【分析】（1）①根据定义，先求出P'，P″的坐标，从而得出Q的位置；
②连接PP'，利用相似三角形的判定和性质可得NTPP′，求出PP′＝OM，即可得结论；
（2）连接PO，并延长至S，使OP＝2OS，延长SQ到T，使ST＝OM，由题意知，PP′∥OM，PP′＝OM，P'N＝2NQ，利用相似三角形的判定和性质得TQ的长，从而求出SQ的长，在△PQS中，PS﹣QS＜PS+QS，则PQ的最小值为PS﹣QS，PQ的最大值为PS+QS，从而解决问题．
【解答】（1）①解：由题意知，P'（﹣3+1，0+1），
∴P'（﹣2，1），
∵点P'关于点N的对称点为P″，N（2，2），
∴P″（6，3），
如图，点Q即为所求；
②证明：连接PP'，
∵∠P'PO＝∠MOx＝45°，
∴PP'∥ON，
∴△QNT∽△QP′P，
∴，
∵P'N＝P″N，P″Q＝QNP″N，
∴QNQP′，
∴NTPP'，
∵PP'，
OM，
∴PP'＝OM，
∴NTOM；
（2）解：如图，连接PO，并延长至S，使OP＝2OS，延长SQ到T，使ST＝OM，
由题意知，PP'∥OM，PP'＝OM，P'N＝2NQ，
∴△P′MN∽△P′TQ，
∴，
∴TQMN，
∵MN＝OM﹣ON＝2﹣t，
∴TQ＝3t，
∴SQ＝ST﹣TQ＝2﹣（3t）t﹣1，
∵PS﹣QS≤PQ≤PS+QS，
∴PQ的最小值为PS﹣QS，PQ的最大值为PS+QS，
∴PQ长的最大值与最小值的差为（PS+QS）﹣（PS﹣QS）＝2QS＝3t﹣2．
【点评】本题是圆的综合题，主要考查了相似三角形的判定和性质，三角形三边关系，平移的性质等知识，解题的关键是理解定义，画出图形，利用相似三角形的判定和性质求出QT的长是解题的关键．
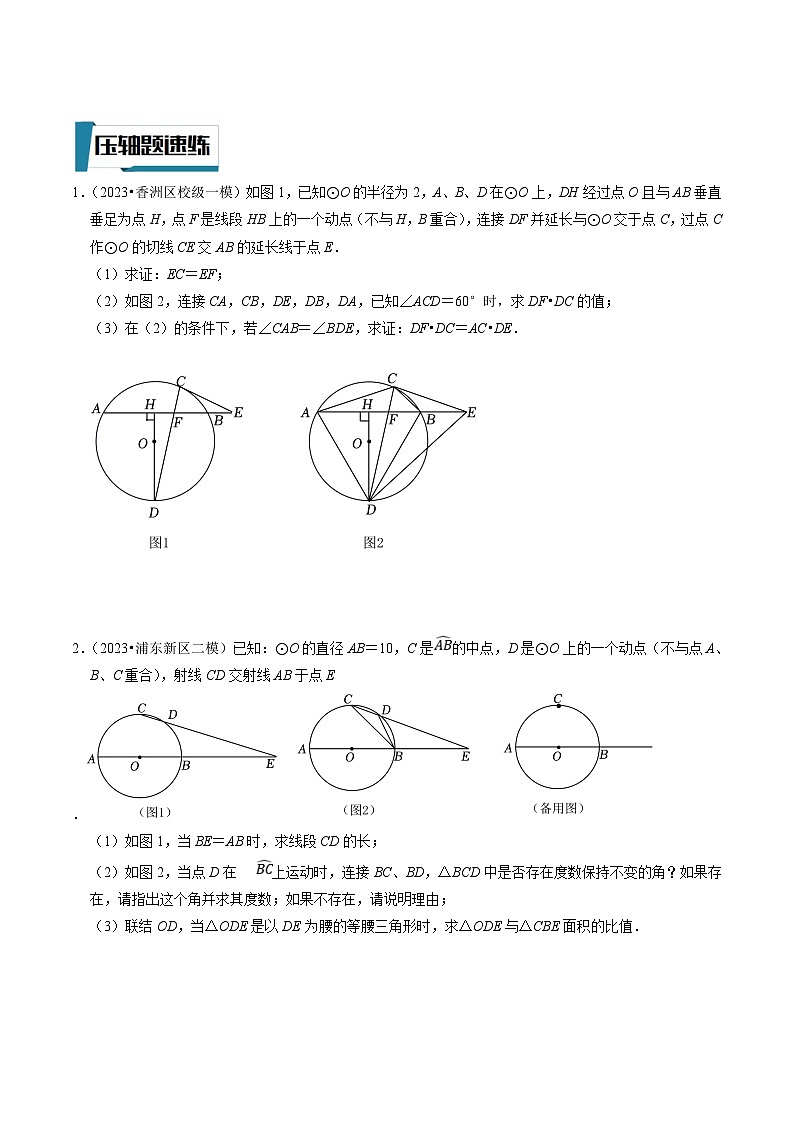
1．（2023•香洲区校级一模）如图1，已知⊙O的半径为2，A、B、D在⊙O上，DH经过点O且与AB垂直垂足为点H，点F是线段HB上的一个动点（不与H，B重合），连接DF并延长与⊙O交于点C，过点C作⊙O的切线CE交AB的延长线于点E．
（1）求证：EC＝EF；
（2）如图2，连接CA，CB，DE，DB，DA，已知∠ACD＝60°时，求DF•DC的值；
（3）在（2）的条件下，若∠CAB＝∠BDE，求证：DF•DC＝AC•DE．
【分析】（1）连接OC，根据切线的性质得到，∠OCD+∠ECD＝90°，根据垂直及同圆的半径相等得到∠CFE＝∠ECD，进而证明EC＝EF；
（2）连接OB，根据同弧所对的圆周角相等，先证明△ABD为等边三角形，然后证明△BDC∽△FDB，推比例线段，求DF•DC的值；
（3）证明△CAB～△BDE，推比例线段，等量代换后得出BD2＝AC•DE，再根据（2）DF•DC＝DB2，等量代换后得出DF•DC＝AC•DE．
【解答】（1）证明：连接OC，如图所示：
∵⊙O的切线是CE，
∴∠OCD+∠ECD＝90°，
∵DH⊥AB，
∴∠HDB+∠HFD＝90°，
∵OD＝OC，
∴∠HDC＝∠CFE，
∴∠CFE＝∠ECD，
∴EC＝EF；
（2）解：连接OB，如图所示：
∵∠ACD＝60°，，
∴∠ACD＝∠ABD＝60°，
∵DH⊥AB且DH过圆心，
∴AH＝BH，
∴DB＝DA，
∴△ABD为等边三角形，
在Rt△OBH中，∠BOH＝60°，OB＝2，
∴OHOB＝1，
∴BH，
∴∠BCD＝∠DBF＝60°，
AD＝AB＝BD＝2BH＝2，
∠BDC＝∠FDB，
∴△BDC∽△FDB，
∴，
∴DF•DC＝DB2＝12；
（3）证明：∵△ABD为等边三角形，
∴∠ACD＝∠DBF＝60°，AD＝AB＝DB，
∴∠ACB＝∠DBE＝120°，
∵∠CAB＝∠BDE，
∴△CAB～△BDE，
∴，
∴，
∴DB2＝AC•DE，
∵DF•DC＝DB2，
∴DF•DC＝AC•DE．
【点评】此题属于圆的综合题，考查了三角形相似的判定和性质、切线的性质、垂径定理、等边三角形的判定和性质，解题关键是找到三角形相似的条件．
2．（2023•浦东新区二模）已知：⊙O的直径AB＝10，C是的中点，D是⊙O上的一个动点（不与点A、B、C重合），射线CD交射线AB于点E．
（1）如图1，当BE＝AB时，求线段CD的长；
（2）如图2，当点D在上运动时，连接BC、BD，△BCD中是否存在度数保持不变的角？如果存在，请指出这个角并求其度数；如果不存在，请说明理由；
（3）联结OD，当△ODE是以DE为腰的等腰三角形时，求△ODE与△CBE面积的比值．
【分析】（1）连接OC、BC、AD，由勾股定理求出CE，由△AED∽△CEB求出DE，则CD＝CE﹣DE．
（2）∠BDC不变，连接AC，则∠CAB＝45°，由圆内接四边形的对角互补得∠BCD＝135°．
（3）①当 DE＝DO时，证明△OCD是等边三角形，求出CD＝OC＝DE＝5，由勾股定理求出OE，分别求出两个三角形的面积作比即可得到结果．②DE＝OE不成立．
【解答】（1）解：如图1，连接OC、BC、AD，
∵C是的中点，OC是半径，
∴OC⊥AB，
∵BE＝AB＝10，
∴AE＝AB+BE＝20，OE＝OB+BE＝5+10＝15，
∴CE，
∵∠DAE＝∠BCE，∠AED＝∠CEB，
∴△ADE∽△CBE，
∴，
∴，
∴DE，
∴CD＝CE﹣DE．
（2）∠BDC不变，∠BDC＝135°．
如图2，连接AC，
∵C是的中点，
∴AC＝BC，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∴∠CAB＝45°，
∵∠CAB+∠BDC＝180°，
∴∠BDC＝180°﹣∠CAB＝180°﹣45°＝135°．
（3）解：①如图3，当 DE＝DO时，
∵AB＝10，
∴OD＝OC＝DE＝5，
∵C是的中点，
∴OC⊥AB，
∴∠DOE+∠COD＝90°，
∠DEO+∠OCD＝90°，
∵DE＝DO，
∴∠DOE＝∠DEO，
∴∠COD＝∠OCD，
∴CD＝OD，
∴CD＝OD＝OC，
∴△OCD是等边三角形，
∴CE＝DE＝5，CE＝10，
∴OE，
∴BE＝OE﹣OB，
∴S△ODES△COEOC•OE5，
S△CBEOC•BE5×（5），
∴．
②DE＝OE不成立．
∵∠DOE＝90°﹣∠COD，
∠ODE＝180°﹣∠CDO＝180°（180°﹣∠COD）＝90°+∠COD，
∴∠ODE＞∠DOE，
∴DE≠OE．
综上得，△ODE与△CBE面积的比值为：．
【点评】本题考查了圆中垂径定理，圆内接四边形的性质，三角形相似，勾股定理等知识，综合性较强，解答本题需要我们熟练掌握各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．
3．（2023春•海陵区月考）古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”．小明决定研究一下圆，如图，AB是⊙O的直径，点C是⊙O上的一点，延长AB至点D，连接AC、BC、CD，且∠CAB＝∠BCD，过点C作CE⊥AD于点E．
（1）求证：CD是⊙O的切线；
（2）若OB＝BD，求证：点E是OB的中点；
（3）在（2）的条件下，若点F是⊙O上一点（不与A、B、C重合），求的值．
【分析】（1）要证明CD是⊙O的切线，只需证明∠OCD＝90°，即OC⊥CD即可；
（2）利用直角三角形斜边中线的性质证明△OCB是等边三角形，利用等边三角形的性质即可得到结论；
（3）连接OF，由，∠EOF＝∠FOD，证明△EOF∽△FOD，即可得到答案．
【解答】（1）证明：连接OC，
∵AB是⊙O的直径，
∴∠ACB＝90°，
∵OA＝OC，
∴∠CAB＝∠ACO，
∵∠CAB＝∠BCD，
∴∠BCD＝∠ACO，
∴∠BCD+∠OCB＝∠ACO+∠OCB＝∠ACB＝90°，即∠OCD＝90°，
∴OC⊥CD，
∵OC是⊙O的半径，
∴CD是⊙O的切线；
（2）证明：∵OB＝BD，∠OCD＝90°，
∴，
∵OB＝OC，
∴BC＝OB＝OC，
∴△OCB是等边三角形，
∵CE⊥AD，
∴，
∴点E是OB的中点；
（3）解：连接OF，
则OF＝OB，而，OB＝BD，
∴，，
∴，
∵∠EOF＝∠FOD，
∴△EOF∽△FOD，
∴，
即的值为．
【点评】本题考查了切线的判定，圆周角定理，等边三角形的判定和性质，相似三角形的判定和性质，解题的关键是灵活运用所学知识解决问题．
4．（2023春•长沙期中）如图1，四边形ABCD中，∠ADC＝120°，∠ABC＝150°，且，BD＝4．
（1）求∠DCB的度数；
（2）如图2，连接AC，求AC2；
（3）如图3，四边形ABCD内接于⊙O，∠A＝90°，上存在点E，满足，连结BE并延长交CD的延长线于点F，BE与AD交于点G，连结CCE，CE＝BG．若，用含字母a的式子表示△DEF的周长．
【分析】（1）过B作BK⊥CD于K，由∠ADC＝120°，AD⊥BD，得∠KDB＝120°﹣90°＝30°，即知BKBD＝2，CK2，故CK＝BK，从而∠DCB的度数为45°；（2）过C作CR⊥AB交AB延长线于R，由∠DCB＝45°，可得∠DAB＝360°﹣∠ADC﹣∠DCB﹣∠ABC＝45°，△ABD是等腰直角三角形，即得ABBD＝4，又∠CBR＝180°﹣∠ABC＝30°，得CRBC，BRCR，在Rt△ACR中，用勾股定理可得AC2＝40+16；
（3）连接DE，BD，由∠A＝90°，可得∠BED＝90°，∠DEF＝90°，而tan∠ADB，知ABa，又，可得AD＝BG＝CE＝a，故AGa，DG＝AD﹣AGa，即可得∠ABG＝∠ADE＝30°＝∠CED，从而GEDGa，DEGEa，证明△BGD≌△CEF（ASA），可得EF＝DGa，即得DFa，从而△DEF的周长＝DE+EF+DFaaa．
【解答】解：（1）过B作BK⊥CD于K，如图：
∵∠ADC＝120°，AD⊥BD，
∴∠KDB＝120°﹣90°＝30°，
∴BKBD4＝2，
在Rt△BCK中，
CK2，
∴CK＝BK，
∴∠KBC＝∠C＝45°，
∴∠DCB的度数为45°；
（2）过C作CR⊥AB交AB延长线于R，如图：
由（1）知∠DCB＝45°，
∴∠DAB＝360°﹣∠ADC﹣∠DCB﹣∠ABC＝45°，
∴△ABD是等腰直角三角形，
∴ABBD＝4，
∵∠CBR＝180°﹣∠ABC＝30°，
∴CRBC，BRCR，
∴AR＝AB+BR＝4，
在Rt△ACR中，
AC2＝AR2+CR2＝（4）2+（）2＝40+16；
∴AC2＝40+16；
（3）连接DE，BD，如图：
∵∠A＝90°，
∴BD为直径，
∴∠BED＝90°，∠DEF＝90°，
∵tan∠ADB，AD＝a，
∴ABa，
∵，
∴，∠ABE＝∠CED，
∴AD＝CE，
∵CE＝BG，
∴AD＝BG＝CE＝a，
∴AGa，
∴DG＝AD﹣AG＝aaa，
∵sin∠ABE，
∴∠ABG＝∠ADE＝30°＝∠CED，
∴GEDGa，DEGEa，
∵∠BGD＝∠A+∠ABE＝90°+30°＝120°，∠CEF＝∠CED+∠DEF＝120°，
∴∠BGD＝∠CEF，
在△BGD和△CEF中，
，
∴△BGD≌△CEF（ASA），
∴EF＝DGa，
∴DFa，
∴△DEF的周长＝DE+EF+DFaaa．
【点评】本题是圆的综合题，考查了圆的有关知识，全等三角形的判定和性质，锐角三角函数，直角三角形的性质等知识，解题的关键是作辅助线，构造直角三角形解决问题．
5．（2023•花都区一模）如图，⊙O是△ABC的外接圆，直径AB＝10，BC＝8，AE平分∠CAB交BC于点E．
（1）尺规作图：在AE的延长线上取一点F，使得BF＝BE，连接BF；（保留作图痕迹，不写作法）
（2）在（1）所作的图中：
①证明：BF是⊙O的切线；
②求的值．
【分析】（1）以B为圆心，以BE的长为半径画弧，交AE的延长线于点F即可．
（2）①先证∠ABF＝90°，再由OB是半径即可得结论．②先证△BEG∽△BAC，得出EG的长，再证△AEG∽△AFB即可．
【解答】（1）如图1，以B为圆心，以BE的长为半径画弧，交AE的延长线于点F，
则点F即为所求．
（2）①证明：∵AB是⊙O的直径，
∴∠C＝90°，
∴∠CAE+∠AEC＝90°，
∵BF＝BE，
∴∠BEF＝∠BFE，
∵∠AEC＝∠BEF，
∴∠AEC＝∠BFE，
∴∠CAE+∠BFE＝90°，
∵AE平分∠CAB，
∴∠CAE＝∠BAF，
∴∠BAF+∠BFE＝90°，
∴∠ABF＝90°，
又∵OB是半径，
∴BF是⊙O的切线．
②解：如图2，过点E作EG⊥AB，垂足为G，
∵∠C＝90°，AE平分∠CAB，
∴EG＝CE，
∴BE＝BC﹣CE＝BC﹣EG＝8﹣EG，
∵∠C＝90°，
∴AC6．
∵∠EGB＝∠C＝90°，∠EBG＝∠ABC，
∴△BEG∽△BAC，
∴，
∴，
解得EG＝3，
∴BE＝BC﹣EG＝8﹣3＝5，
∴BF＝BE＝5，
∵∠AEG＝∠ABF＝90°，
∴△AEG∽△AFB，
∴，
∴．
【点评】本题主要考查了圆的切线的性质与判定，相似三角形的性质与判定等知识，把所学知识融会贯通，灵活运用是解题的关键．
6．（2023•碑林区校级模拟）如图①，已知线段AB与直线l，过A、B两点，作⊙O使其与直线l相切，切点为P，易证∠APB＝∠AHB＞∠AQB，可知点P对线段AB的视角最大．
问题提出
（1）如图②，已知△ABP的外接圆为⊙O，PQ与⊙O相切于点P，交AB的延长线于点Q．
①请判断∠BPQ与∠A的大小关系，并说明理由．
②若QB＝2，AB＝6，求PQ的长．
问题解决
（2）如图③，一大型游乐场入口AB设在道路DN边上，在“雪亮工程”中，为了加强安全管理，结合现实情况，相关部门准备在与地面道路DN夹角为60°的射线DM方向上（位于垂直于地面的平面内）确定一个位置C，并架设斜杆AC，在斜杆AC的中点P处安装一摄像头，对入口AB实施监控（其中点A、B、D、P、C、M、N在同一平面内），已知DA＝40米，AB＝25米，调研发现，当∠APB最大时监控效果最好，请问在射线DM上是否存在一点C，使得∠APB达到最大？若存在，请确定点C在DM上的位置及斜杆AC的长度；若不存在，请说明理由．
【分析】（1）①作直径PN，连接BN，则∠PNB+∠NPB＝90°，PQ与⊙O相切，得∠NPB+∠BPQ＝90°，再根据圆周角定理即可得结果．②证明△BPQ∽△PAQ，得，代入数值可得结果．
（2）取AD的中点E，过点E作DM的平行线EF，经过A，B作⊙O与EF相切于点P，此时∠APB最大，由△PEA∽BEP求出PE，由勾股定理求出EH，AH，PE，再求出PA，最终得到CD，AC的长度．
【解答】（1）解：①∠BPQ＝∠A，理由如下：
如图②，连接PO并延长至圆上一点N，连接BN，
则∠PAB＝∠PNB，
∵PN为圆的直径，
∴∠PBN＝90°，
∴∠PNB+∠NPB＝90°，
∵PQ与⊙O相切于点P，
∴∠NPQ＝90°，
∴∠NPB+∠BPQ＝90°，
∴∠BPQ＝∠PNB，
∵∠PNB＝∠A，
∴∠BPQ＝∠A．
②∵∠BPQ＝∠A，∠BQP＝∠PQA，
∴△BPQ∽△PAQ，
∴，
∵AB＝6，QB＝2，
∴AQ＝AB+BQ＝6+2＝8，
∴，
∴PQ＝4．
（2）解：存在一点C，使得∠APB达到最大．
如图③，取AD的中点E，过点E作DM的平行线EF，
经过A，B作⊙O与EF相切于点P，
由题意知，此时∠APB最大．
∵DM∥EF，P是AC中点，
∴∠PEA＝60°，CD＝2PE，
作直径PG，连接AG，
则∠PBE＝∠G，∠PAC＝90°，
∴∠APG+∠PBE＝90°，
∵EF是⊙O的切线，P是切点，
∴PG⊥EF，
∴∠EPA+∠APG＝90°，
∴∠EPA＝∠PBE，
又∠AEP＝∠PEB，
∴△PEA∽BEP，
∴PE2＝EA•EB＝20×（20+25）＝900，
∴PE＝30，
∴CD＝2PE＝60．
过点A作AH⊥EF于H，
∵∠PEA＝60°，
∴∠EAH＝30°，
∴EHAE20＝10，
AH＝AE•sin60°＝2010，
∴PH＝PE﹣EH＝30﹣10＝20，
由勾股定理得，
PA，
∴AC＝2PA＝2．
故点C在DM上距离点D60m处，斜杆AC的长度为m．
【点评】本题考查了圆周角定理，切线的性质，三角形相似，圆的张角等知识，属于圆的综合题，恰当添加辅助线，灵活运用所学知识是解题关键．
7．（2023春•西城区校级月考）在平面直角坐标系xOy中，对于点C和圆P，给出如下定义：
若圆P上存在A、B两点，使得△ABC是等腰直角三角形，且∠ABC＝90°，则称点C是圆P的“等垂点”．
（1）当点P坐标为（3，0），且圆P的半径为2时．
①如图1，若圆P上存在两点A（1，0）和B（3，2），请直接写出此时圆P的“等垂点”C的坐标 （1，4），（5，0） ；
②如图2，若直线y＝x+b上存在圆P的“等垂点”，求b的取值范围；
（2）设圆P的圆心P在y轴上，半径为2．
若直线y＝﹣x上存在点R，使半径为1的圆R上有点S是圆P的“等垂点”，请直接写出圆心P的纵坐标的取值范围．
【分析】（1）①连接BP，AB，连接BC2，过A点作AC1⊥AC2交C2B的延长线于点C1，再根据“等垂点”定义即可作答；②当直线y＝x+b再圆P上方时，此时以直径AB为腰构造等腰Rt△ABC1，此时使得点C1刚好在直线y＝x+b上，此时为上临界位置，即可求出C1（1，4），将C1（1，4）代入直线y＝x+b，可得b＝3；当直线y＝x+b再圆P下方时，此时以直径AB为腰构造等腰Rt△ABC2，此时使得点C2刚好在直线y＝x+b上，此时为下临界位置，问题即可求解；
（2）随着圆R的移动，圆R的覆盖区域为直线y1＝﹣x+a与直线y2＝﹣x+b所夹的区域，再求出即直线y2＝﹣x+b解析式为：，直线y1＝﹣x+a解析式为：，当圆P位于x轴的上方时，此时以直径AB为腰构造等腰Rt△ABS，此时使得点S刚好在直线直线上，为上临界位置；当圆P位于x轴的下方时，此时以直径AB为腰构造等腰Rt△ABS，此时使得点S刚好在直线直线上，为下临界位置，画出图形即可求解．
【解答】解：（1）①∵点P坐标为（3，0），且圆P的半径为2，
∴圆P的与x轴的交点为：A（1，0），C2（5，0），
连接BP，AB，连接BC2，过A点作AC1⊥AC2交C2B的延长线于点C1，如图，
∵B（3，2），点P坐标为（3，0），
∴BP⊥AC2，
∵AC2为圆P的直径，BP＝AP＝PC2，
∴∠ABC2＝90°，∠BC2P＝45°，
∴△BC2A是等腰直角三角形，
∵AC1⊥AC2，
∴∠C1AC2＝90°，
∴∠AC1C2＝45°，即△C1AC2是等腰直角三角形，
∴AC1＝AC2＝4，
∵∠ABC2＝90°，
∴∠ABC1＝90°，
∴△BC1A是等腰直角三角形，
综上：即圆P的“等垂点”为点C1和C2，
∵AC1＝4，AC1⊥AC2，A（1，0），
∴C1（1，4），
故答案为：（1，4），（5，0）；
②当直线y＝x+b再圆P上方时，此时以直径AB为腰构造等腰Rt△ABC1，
此时使得点C1刚好在直线y＝x+b上，此时为上临界位置，如图，
即有：B（1，0），A（5，0），BC1＝AB＝4，BC1⊥AB，
∴C1（1，4），
∵C1（1，4）在直线y＝x+b上，
∴y＝1+b＝4，即b＝3；
当直线y＝x+b再圆P下方时，此时以直径AB为腰构造等腰Rt△ABC2，
此时使得点C2刚好在直线y＝x+b上，此时为下临界位置，如图，
即有：A（1，0），B（5，0），BC2＝AB＝4，BC2⊥AB，
∴C2（5，﹣4），
∵C2（5，﹣4）在直线y＝x+b上，
∴y＝5+b＝﹣4，即b＝﹣9；
综上：b的取值范围：﹣9≤b≤3；
（2）随着圆R的移动，圆R的覆盖区域为直线y1＝﹣x+a与直线y2＝﹣x+b所夹的区域，如图所示，
+
即有直线y1＝﹣x+a与直线y2＝﹣x+b均与圆R相切，
设直线y2＝﹣x+b与x轴交于点F，与y轴交于点N，过O点作直线y2＝﹣x+b的垂线OE，交于直线y2＝﹣x+b于点E（也为切点），
当y2＝0时，x＝b，当x＝0时，y2＝b，
∴ON＝OF＝|b|＝b，
∴△NOF是等腰直角三角形，
∵圆R的半径为1的，
∴OE＝1，
∴，
∴，
∴即直线y2＝﹣x+b解析式为：，
同理可得：直线y1＝﹣x+a解析式为：，
当圆P位于x轴的上方时，此时以直径AB为腰构造等腰Rt△ABS，
此时使得点S刚好在直线直线上，为临界位置，
如图，
+
∵圆P的圆心P在y轴上，半径为2，
∴AB＝4，
∴BS＝AB＝4，
∴点S的横坐标为：﹣4，
∴，即，
∴；
当圆P位于x轴的下方时，此时以直径AB为腰构造等腰Rt△ABS，
此时使得点S刚好在直线直线上，为临界位置，
如图，
同理可求得：；
即：圆心P的纵坐标的取值范围为：．
【点评】本题是一道与圆相关的综合题，考查了一次函数的性质，圆与直线的位置关系，等腰三角形的性质等知识，还运用到了解直角三角形的知识，正确理解“等垂点”的含义是解答本题的关键．
8．（2023•花都区一模）如图1，已知∠MAN＝60°，在射线AM、AN上分别截取点B、C，使AB＝AC＝8．
（1）求证：AB＝BC；
（2）如图2，以BC为直径在BC的上方作一个半圆，点D为半圆上的一个动点，连接AD交BC于点E．
①当DB⊥AB时，求AD的长．
②在线段AC上取一点F，连接BF交AD于点G，若BF＝AE，当点D在半圆BC上从点B运动到点C时，求点G经过的路径长．
【分析】（1）证明△ABC是等边三角形即可得到结果．
（2）连接CD，则∠BDC＝90°，∠CBD＝30°，先求出BD，再利用勾股定理即可求出AD．
（3）分类讨论：当∠BFA＝∠AEB时，证明△ABF≌△BAE得到BG＝AG，点G在AB边的中垂线上，求出△ABC的高即可．②当∠BFC＝∠AEB时，△BCF≌△ABE，此时点D经过的路径为图中以BA为弦的弧长，求出弧的圆心角，半径，再求出弧长即可．
【解答】（1）证明：∵∠MAN＝60°，AB＝AC，
∴△ABC是等边三角形，
∴AB＝BC．
（2）解：如图2，连接CD，
∵DB⊥AB，
∴∠ABD＝∠ABC+∠CBD＝90°，
∵△ABC是等边三角形，
∴∠ABC＝60°，BC＝AB＝6，
∴∠CBD＝30°，
∵点D为半圆上的一个动点，
∴∠BDC＝90°，
∴CDBC8＝4，
∴BD，
∴AD．
（3）解：∵△ABC是等边三角形，
∴∠BAC＝ABC＝60°，AB＝BC＝AC＝8，
①如图3，当∠BFA＝∠AEB时，
∵∠BAC＝∠ABC，BF＝AE，
∴△ABF≌△BAE（AAS），
∴∠FBA＝∠EAB，
∴BG＝AG，
∴点G在AB边的中垂线上，
此时点G经过的路径为AC•sin60°＝84．
②如图4，∠BFC＝∠AEB时，即∠BFA+∠AEB＝180°时，
∵∠ABC＝∠ACB＝60°，AB＝BC，
∴△BCF≌△ABE（AAS），
∴∠CBF＝∠BAE，
此时点D经过的路径为图中以BA为弦的弧长，
最高点G在AB边中垂线上，线段CP的处．
∴GPCPAC•sin60°8．
设弦AB所在圆的半径为r，由垂径定理得，
r2＝（r）2+4，
解得，r，
∴弦AB所对的圆心角为120°
∴弧AB的长ππ．
综上得，点G经过的路径长为或．
【点评】本题考查了圆周角定理，等边三角形的判定与性质，全等三角形的判定与性质，勾股定理，弧长计算公式等知识，合理进行分类讨论，准确找到点的运动轨迹是解题关键．
9．（2023•长沙模拟）如图，AB为⊙O的直径，弦CD⊥AB于点F，且C为的中点，AE交CD于点G，若AF＝2，AE＝8，动点M是⊙O上一点，过点D作⊙O的切线，交BA的延长线于点P．
（1）求CF的长；
（2）连接OG，求证：OG⊥AC；
（3）当动点M在⊙O的圆周上运动时，的比值是否发生变化？若不变，求出比值；若变化，说明变化规律．
【分析】（1）由垂径定理得出，证出AE＝DC＝8，则可得出答案；
（2）利用圆周角定理得出，∠DCF＝∠EFB，进而得出∠DCF＝∠AFC，再利用三角形中位线定理得出答案；
（3）分别利用当点M与点A重合时：，当点M与点B重合时：，当点M不与点A、B重合时，得出△OFM∽△OPM，分别得出答案．
【解答】（1）解：∵C为的中点，弦CD⊥AB于F，
∴，
∴，
∴AE＝DC＝8，
∴CF＝DF＝4，
（2）证明：连接AC，BC，OG，BC交AE于点N，
∵，
∴∠EBC＝∠EAC＝∠DCA＝∠CBA，
∵∠BFE+∠EBC＝90°，∠ABC+∠DCB＝90°，
∴AG＝GC，∠DCB＝∠EFB，
∴∠DCB＝∠ANC，
∴GN＝GC，
∵AO＝BO，
∴OG是△OAN的中位线，
∴GO∥BC，
∵AB为⊙O的直径，
∴BC⊥AC，
∴OG⊥AC；
（3）解：的值不变．
理由：如图2，连接DO，则DO⊥PD，DF⊥PO，
∵∠OFD＝∠ODP，∠FOD＝∠POD，
∴△OFD∽△ODP，
同理△OFD∽△DFP，
则DO2＝FO•OP，
DF2＝OF•FP，
由（1）知DF＝4，
设AO＝x，则FO＝x﹣2，
故x2＝（x﹣2）2+42，
解得：x＝5，故FO＝3，
即42＝3•FP，
∴FP．
当点M与点A重合时：，
当点M与点B重合时：，
当点M不与点A、B重合时：连接FM、PM、MO、DO，
∵DO2＝FO•OP，
∴OM2＝FO•OP，
∴，
∵∠AOM＝∠MOA，
∴△OFM∽△OPM，
∴．
综上所述，的比值不变，比值为．
【点评】本题是圆的综合题，考查了相似三角形的判定与性质，圆周角定理，垂径定理，三角形中位线定理，熟练掌握相似三角形的判定与性质是解题的关键．
10．（2023•襄都区校级一模）如图，在矩形ABCD中，AB＝12，BC＝8，过DC的中点M作射线AM，点E在射线AM上（点E不与点A重合），点F是AE的中点，以EF为直角边在射线AM的右侧作直角△EFG，其中∠FEG＝90°，tan∠EGF．⊙O是△EFG的外接圆，设⊙O的半径为r．
（1）用含r的代数式表示EF的长；
（2）当⊙O与矩形ABCD的边相切时，求r的值；
（3）当边EG与矩形ABCD的边有交点时，请直接写出符合条件的整数r的值．
【分析】（1）根据tan∠EGF，设EF＝3x，EG＝4x，运用勾股定理即可求得答案；
（2）分四种情况：当⊙O与矩形ABCD的边AB相切时，过点O作OH⊥AB于点H，过点F作FK⊥AB于点K，由切线性质可得OH＝FK＝r，再利用解直角三角形可得出AFr，与AF＝EFr矛盾，故⊙O不能与AB边相切；显然⊙O也不能与AD边相切；当⊙O与矩形ABCD的边CD相切时，由AFr，可得FK＝AF•sin∠FAKr•sin∠AMDr•r，利用切线性质可得FN＝OH＝r，根据FN+FK＝NK，建立方程求解即可求得r；当⊙O与矩形ABCD的边BC相切时，同理可求得r；
（3）当点E与点M重合时，根据EFr＝5，解方程即可求得求得EG与矩形ABCD的边有交点时r的最小值，当EG经过点C时，可得AE＝2EFr，再利用解直角三角形可得EM，根据AE＝AM+EM，建立方程求解即可求得EG与矩形ABCD的边有交点时r的最大值，得出当EG与矩形ABCD的边有交点时，r，再求出整数值．
【解答】解：（1）∵tan∠EGF，
∴，
设EF＝3x，EG＝4x，
在Rt△EFG中，EF2+EG2＝FG2，
∴（3x）2+（4x）2＝（2r）2，
解得：xr（负值舍去），
∴EF＝3xr；
（2）当⊙O与矩形ABCD的边AB相切时，如图1，过点O作OH⊥AB于点H，过点F作FK⊥AB于点K，
∵四边形ABCD是矩形，AB＝12，BC＝8，
∴AD＝BC＝8，CD＝AB＝12，∠BAD＝∠ADC＝90°，AB∥CD，
∴∠FAK＝∠AMD，
∵点M是DC的中点，
∴DMCD＝6，
∴tan∠FAK＝tan∠AMD，
∵tan∠EFG，
∴tan∠FAK＝tan∠EFG，
∴∠FAK＝∠EFG，
∴FG∥AB，
∴FK＝OH，
∵AB与⊙O相切，
∴OH＝r，
∴FK＝r，
在Rt△ADM中，AM10，
∵sin∠FAK＝sin∠AMD，
∴，即，
∴AFr，
∵点F是AE的中点，
∴AF＝EFr，
由（1）知EFr，矛盾，
故⊙O不能与AB边相切；
⊙O也不能与AD边相切；
当⊙O与矩形ABCD的边CD相切时，如图2，过点O作OH⊥CD于点H，过点F作FK⊥AB于点K，
∵CD与⊙O相切，
∴OH＝r，
由（1）EFr，
∴AFr，
∴FK＝AF•sin∠FAKr•sin∠AMDr•r，
∵FG∥AB，AB∥CD，
∴FG∥CD，
∴FN＝OH＝r，
∵∠BAD＝∠ADC＝∠AKN＝90°，
∴四边形ADNK是矩形，
∴NK＝AD＝8，
∵FN+FK＝NK，
∴rr＝8，
解得：r；
当⊙O与矩形ABCD的边BC相切时，如图3，过点O作OH⊥CD于点H，过点F作FK⊥AB于点K，
则FG＝2r，AF＝EFr，
AK＝AF•cs∠FAK＝AF•cs∠AMDr•r，
∵∠FKB＝∠B＝∠BGF＝90°，
∴四边形BGFK是矩形，
∴BK＝FG＝2r，
∵AK+BK＝AB，
∴r+2r＝12，
解得：r；
综上所述，当⊙O与矩形ABCD的边相切时，r的值为或；
（3）当点E与点M重合时，如图4，
∵AM＝2EF＝10，
∴EF＝5，
即r＝5，
解得：r；
当EG经过点C时，如图5，
∵AF＝EFr，
∴AEr，
∵∠CME＝∠AMD，
∴sin∠CME＝sin∠AMD，
∴，即，
∴EM，
∵AE＝AM+EM，
∴r＝10，
解得：r，
∴当EG与矩形ABCD的边有交点时，r，
故符合条件的整数r的值为5．
【点评】本题是有关圆的综合题，考查了圆的性质，圆的切线的性质，解直角三角形，矩形的性质，勾股定理等，运用方程思想和数形结合思想是解题关键．
11．（2023•双桥区模拟）如图，在▱ABCD中，AB＝10，AD＝15，．动点M由点A向点D运动，过点M在AD的右侧作MP⊥AM，连接PA、PD，使∠MPA＝∠BAD，过点A、M、P作⊙O．（参考数据：sin49°，cs41°，tan37°）
（1）当⊙O与DP相切时．
①求AM的长；
②求的长．
（2）当△APD的外心Q在△AMP的内部时（包括边界），求在点M移动过程中，点Q经过的路径的长．
（3）当△APD为等腰三角形，并且线段PD与⊙O相交时，直接写出⊙O截线段PD所得的弦长．
【分析】（1）①根据切线的性质得到AP⊥DP，解直角三角形即可得到结论；
②根据三角函数的定义得到∠PAM＝37°，根据圆周角定理得到∠POM＝2∠PAM＝74°，根据弧长公式即可得到结论；
（2）点Q在AD的垂直平分线上运动，当∠APD＝90°时（图中∠AP′D），点Q在边AD上（Q′），当∠ADP＝90°时（图中∠ADP′）时，点Q在AP上（Q″），点Q运动路径长长是DP″的一半；
（3）当PD＝PA时，⊙O截不出线段PD的弦；当AP＝AD＝15时，解斜三角形APD，求得PD的长，进而得出结果．
【解答】解：（1）①∵DP与⊙O相切，
∴AP⊥DP，
∵，∠MPA＝∠BAD，
∴tan∠PAD，
∴cs∠PAD，
在Rt△ADP中，AP＝AD•cs∠PAD＝1512，
在Rt△APM中，AM＝AP•cs∠PAD＝12；
②∵，
∴∠PAM＝37°，
∴∠POM＝2∠PAM＝74°，
∴的长为；
（2）如图3，设AD的中点为Q′，当点D与M重合时，设AP的中点为Q″，连接Q′Q″，
∵点Q在AD的垂直平分线上运动，当∠APD＝90°时（图中∠AP′D），点Q在边AD上（Q′），当∠ADP＝90°时（图中∠ADP′）时，点Q在AP上（Q″），
∴Q′Q″DP′，
∵AP″＝AD•tan∠DAP″＝15，
∴Q′Q″，
∴点Q的经过的路径长为：；
（3）当PD＝PA时，⊙O截不出线段PD的弦，
如图4，
当AP＝AD＝15时，
设PD与⊙O交于点E，作DG⊥AP于G，连接AE，
由（1）知：AG＝12，DG＝9，
∴PG＝AP﹣AG＝15﹣12＝3，
∵AP是⊙O的直径，
∴∠AEP＝90°，
∴PD3，
∵AD＝AP，
∴PEPD，
∴⊙O截线段PD所得弦的长为．
【点评】本题是圆的综合题，考查了圆周角定理及其推论，弧长公式，解直角三角形，三角形的中位线定理等知识，解决问题的关键是根据条件，画出对应的图形．
12．（2023•崂山区一模）【问题提出】如图1，△ABC为⊙O内接三角形，已知BC＝a，圆的半径为R，探究a，R，sin∠A之间的关系．
【解决问题】如图2，若∠A为锐角，连接BO并延长交⊙O于点D，连接DC，则∠A＝∠D，在△DBC中，BD为⊙O直径，BC＝a，所以BD＝2R，∠BCD＝90°．
所以在Rt△DBC中建立a，R，sinD的关系为 sinD ．
所以在⊙O内接三角形△ABC中，a，R，sinA之间的关系为 sinA ．
类比锐角求法，当∠A为直角和钝角时都有此结论．
【结论应用】
已知三角形△ABC中，∠B＝60°，AC＝4，则△ABC外接圆的面积为 ．
【分析】【解决问题】连接BO并延长交⊙O于点D，连接CD，由圆周角定理得出∠BCD＝90°，由正弦的定义可得出答案；
【结论应用】求出△ABC外接圆的半径，则可得出答案；
【解答】解：【解决问题】△ABC的外接圆半径为R，连接BO并延长交⊙O于点D，连接DC，则∠D＝∠A，
∵BD为⊙O的直径，
∴∠BCD＝90°，
在Rt△DBC中，
∵sinD，
∴sinA．
故答案为：sinD，sinA；
【结论应用】∵∠B＝60°，AC＝4，
∴sinB，
∴，
∴R，
∴△ABC外接圆的面积为．
故答案为：．
【点评】本题是圆的综合题，考查了锐角三角函数的定义，三角形的外接圆，圆周角定理，熟练掌握锐角三角函数的定义是解题的关键．
13．（2023•宁波一模）如图1，AC为▱ABCD的对角线，△ABC的外接圆⊙O交CD于点E，连结BE．
（1）求证：∠BAC＝∠ABE．
（2）如图2，当AB＝AC时，连结OA、OB，延长AO交BE于点G，求证△GOB∽△GBA．
（3）如图3，在（2）的条件下，记AC、BE的交点为点F，连结AE、OF．
①求证：BG2﹣GF2＝GF•EF．
②当时，求sin∠EAG的值．
【分析】（1）根据平行四边形的性质以及圆周角定理即可证明；
（2）由垂径定理证明∠BAG＝∠CAG，再推出∠OAB＝∠OBA＝∠OBG，即可证明结论；
（3）①由△GOB∽△GBA，推出BG2＝GO•GA，再证明△BAG≌△CAG，推出∠ABG＝∠ACG，得到△GCF∽△GEC，推出GC2＝GF•GE，计算即可证明结论；
②设EF＝CF＝7a，得到FG＝9a，GE＝9a，BG＝CG＝12a，由角平分线的性质求得，证明△CEF∽△ABF，求得AB＝28a，由角平分线的性质推出，在Rt△ABH和Rt△OBH中，求得，然后推出∠EAG＝∠OBH，即可求解．
【解答】（1）证明：∵四边形ABCD是平行四边形，
∴AB∥CD，
∴∠ABE＝∠BEC，
∵弧BC＝弧BC，
∴∠BAC＝∠BEC，
∴∠BAC＝∠ABE；
（2）证明：∵AB＝AC，AO经过圆心，
∴∠BAG＝∠CAG，
∵OA＝OB，
∴∠OAB＝∠OBA，
∵∠BAC＝∠ABE，
∴∠OAB＝∠OBA＝∠OBG，
又∠BGO＝∠AGB，
∴△GOB∽△GBA；
（3）①证明：连接CG，
∵△GOB∽△GBA，
∴，
∴BG2＝GO•GA，
∵AB＝AC，∠BAG＝∠CAG，AG＝AG，
∴△BAG≌△CAG（SAS），
∴BG＝CG，∠ABG＝∠ACG，
∵∠ABG＝∠BEC，
∴∠GCF＝∠GEC，
∴△GCF∽△GEC，
∴，
∴GC2＝GF•GE，
∴GF•EF+GF2＝GF（EF+GF）＝GF•GE＝GC2＝BG2，
∴BG2﹣GF2＝GF•EF；
②解：延长AO交BC于点H，
∵∠ABE＝∠ACE＝∠BEC，
∴EF＝FC，
∵，
设EF＝CF＝7a，
则FG＝9a，GE＝16a，
∴BG＝CG12a，
∵，
∴，
∵∠GCF＝∠ECF，即CF是∠ECG的平分线，
∴点F到∠ECG两边的距离相等，
∴，
∴，
∵AB∥CD，
∴△CEF∽△ABF，
∴，
即，
∴AB＝28a，
由（2）可知：OB是∠ABG的平分线，同理，
即，
∴，
设⊙O的半径为R，
∵BG2＝GO•GA，
∴（12a）2，
解得：，
即，
设OH＝x，
在Rt△ABH和Rt△OBH中，（28a）2﹣（R+x）2＝R2﹣x2，
整理得：，
即，
∵∠CAE＝∠CBE，∠CAG＝∠OBG，
∴∠EAG＝∠OBH，
∴．
【点评】本题考查了圆周角定理，解直角三角形，相似三角形的判定和性质，全等三角形的判定和性质，勾股定理，本题难度大，明确题意，找出所求问题需要的条件是解答本题的关键．
14．（2023春•闽侯县期中）如图，点C在以AB为直径的半圆O上（点C不与A，B两点重合），点D是的中点、DE⊥AB于点E，连接AC交DE于点F，连接OF，过点D作半圆O的切线DP交BA的延长线于点P．
（1）求证：AC∥DP；
（2）求证：AC＝2DE；
（3）连接CE，CP，若AE：EO＝1：2，求的值．
【分析】（1）连接OD，由垂径定理得出OD⊥AC，由切线的性质得出OD⊥DP，则可得出结论；
（2）证明△ODE≌△OAM（AAS），由全等三角形的性质得出DE＝AM，则可得出结论；
（3）连接OD，OC，CE，CP，证明△DOE∽△POD，由相似三角形的性质得出，证出△COE∽△POC，得出，则可得出答案．
【解答】（1）证明：连接OD，
∵D为弧AC的中点，
∴OD⊥AC，
又∵DP为⊙O的切线，
∴OD⊥DP，
∴AC∥DP；
（2）证明：∵DE⊥AB，
∴∠DEO＝90°，
由（1）可知OD⊥AC，设垂足为点M，
∴∠OMA＝90°，
∴∠DEO＝∠OMA，AC＝2AM，
又∵∠DOE＝∠AOM，OD＝OA，
∴△ODE≌△OAM（AAS），
∴DE＝AM，
∴AC＝2AM＝2DE；
（3）解：连接OD，OC，CE，CP，
∵∠ODP＝∠OED＝90°，∠DOE＝∠DOP，
∴△DOE∽△POD，
∴，
∴OD2＝OE•OP，
∵OC＝OD，
∴OC2＝OE•OP，
∴，
又∵∠COE＝∠POC，
∴△COE∽△POC，
∴，
∵AE：EO＝1：2，
∴，
∴，
∴．
【点评】本题是圆的综合题，考查的是切线的性质，垂径定理，圆周角定理，相似三角形的判定和性质，全等三角形的判定和性质，掌握圆的切线垂直于过切点的半径及相似三角形的判定与性质是解题的关键．
15．（2023•张家口二模）如图1，在矩形ABCD中，对角线AC和BD相交于点O，OD＝5，sin∠ACB．
（1）如图2，P是对角线AC一点（点P不与两端点重合）．以AP为直径在对角线AC的下方作半圆E，交AB边于点M，连接PM．求cs∠APM＝？
（2）如图3，当半圆E与BC边相切于点F时，连接PF．求tan∠CFP＝？
（3）如图4，点R在BC边上，连接AR，当AR时，求∠CAR＝？
（4）已知点N在AB边或BC边上，且△APN是直角三角形．当同时存在四个符合条件的N点时，请直接写出线段AP的取值范围 AP＜10 ．
【分析】（1）根据直径所对的角是直角，通过平行可得∠APM＝∠ACB，然后可得cs∠APM，
（2）连接AF，EF，根据直径所对的角是直角可得，∠CFP+∠AFB＝90°，根据∠B＝90°，可得∠FAB＝∠CFP，通过EF＝AE，EF和EC的关系，可得EF的值，从而得到BF的值，从而求出解，
（3）过R做RM⊥AC，通过勾股定理，可得BR的长，然后得到CR的长，根据sin∠ACB，得到RM的长，然后求sin∠CAR，得到结果对应的角的度数，
（4）通过分析，∠PAN不能为直角，∠APN为直角只有一个点N满足条件，则要符合4个N点则∠ANP为直角需要有3个满足条件的N点，满足条件的N点即为圆E与AB或BC的交点，则根据（2）问的结果可知，AE，又根据AP＜AC，可得AP的范围．
【解答】解：（1）∵在矩形ABCD中，OD＝5，
∴AC＝BD＝2OD＝10，
∵sin∠ACB．
∴AB＝6，BC＝8，
∵AP是圆E的直径，
∴∠AMP＝90°，
∵矩形ABCD，
∴∠B＝90°，
∴PM∥BC，
∴∠APM＝∠ACB，
∴cs∠APM＝cs∠ACB，
（2）如图，连接EF，AF，
∵AP为圆E的直径，
∴∠AFP＝90°，
∴∠CFP＝∠AFB＝90°，
∵∠B＝90°，
∴∠FAB+∠AFB＝90°，
∴∠FAB＝∠CFP，
∵EF＝EA，
∴CE＝AC﹣AE＝10﹣EF，
∵BC与圆E切于F点，
∴EF⊥CF，
∴在Rt△CEF中，
sin∠ACB，
，
∴EF，
∴CF＝5，
∴BF＝BC﹣CF＝8﹣5＝3，
∴tan∠CFP＝tan∠FAB，
（3）如图，过R作RM⊥AC交AC于M，
在Rt△ABR中，
BR，
∴CR＝BC﹣BR，
在Rt△CRM中，
MR＝CR•sin∠ACB，
在Rt△AMR中，
sin∠MAR，
∴∠MAR＝45°，
（4）∵△APN为直角三角形，
∵∠PAN≠90°，
∴∠APN＝90°或∠ANP＝90°，
∵AP是圆E的直径，
∴∠ANP＝90°时，N点为圆E与AB或BC边的交点，
当∠APN＝90°时，则只有一个对应的N点，
∴若有4个满足条件的N点，则圆E与AB或BC边有3个交点，
∴由（2）问可知，AE，
∴AP，
∵P是对角线AC上的一点，且不与端点重合，
∴AP＜AC，
∴AP＜10，
∴AP＜10．
【点评】本题主要考查圆的相关知识，直径对应的圆周角为直角，正弦定理，余弦定理．
16．（2023•慈溪市一模）如图，四边形ABCD内接于⊙O，AB＝AD，AC为直径，E为一动点，连结BE交AC于点G，交AD于点F，连结DE．
（1）设∠E为α，请用α表示∠BAC的度数．
（2）如图1，当BE⊥AD时，
①求证：DE＝BG．
②当，BG＝5时，求半径的长．
（3）如图2，当BE过圆心O时，设tan∠ABE＝x，，求y关于x的函数表达式．
【分析】（1）由AB＝AD，得，则∠ACB＝∠ACD，由AC是⊙O的直径，得∠ABC＝∠ADC＝90°，则∠BAC+∠ACB＝90°，∠DAC+∠ACD＝90°，所以∠BAC＝∠DAC∠BADα；
（2）①连结BD，由∠AFB＝∠ADC＝90°，得BE∥CD，则∠DBE＝∠BDC，所以，则DE＝BC，而∠BGC＝∠ACD＝∠ACB，则BC＝BG，所以DE＝BG；
②作GL⊥AB于点L，则GL＝GF，tan∠ABE，设GL＝GF＝3m，BL＝4m，则BG＝5m，BF＝8m，所以AF＝BF•tan∠ABE＝6m，则tan∠BAC＝tan∠DAC，而BC＝BG＝5，所以AB＝2BC＝2×5＝10，由勾股定理得AC＝5，即可求得⊙O的半径的长为；
（3）连结BD交AC于点M，由垂径定理得AC⊥BD，MB＝MD，因为OB＝OE，所以OM∥ED，ED＝2OM，由△AOF∽△DEF，得，可推导出，则y1，因为∠AMB＝∠BMC＝90°，∠ABE＝∠BAC＝∠DAC＝∠DBC，所以tan∠ABE＝x，设AM＝a，则BM＝ax，CM＝x•BM＝ax2，所以AC＝a+ax2，OA，OM，则y1．
【解答】解：（1）∵AB＝AD，
∴，
∴∠ACB＝∠ACD，
∵AC是⊙O的直径，
∴∠ABC＝∠ADC＝90°，
∴∠BAC+∠ACB＝90°，∠DAC+∠ACD＝90°，
∵∠BAD＝∠E＝α，
∴∠BAC＝∠DAC∠BADα．
（2）①证明：如图1，连结BD，
∵BE⊥AD于点F，
∴∠AFB＝∠ADC＝90°，
∴BE∥CD，
∴∠DBE＝∠BDC，
∴，
∴DE＝BC，
∵∠BGC＝∠ACD＝∠ACB，
∴BC＝BG，
∴DE＝BG．
②如图1，作GL⊥AB于点L，则GL＝GF，∠BLG＝90°，
∴tan∠ABE，
设GL＝GF＝3m，BL＝4m，则BG5m，
∴BF＝5m+3m＝8m，
∴AF＝BF•tan∠ABE＝8m6m，
∴tan∠BAC＝tan∠DAC，
∵BC＝BG＝5，
∴AB＝2BC＝2×5＝10，
∴AC5，
∴OAAC5，
∴⊙O的半径的长为．
（3）如图2，连结BD交AC于点M，
∵AC是⊙O的直径，，
∴AC⊥BD，MB＝MD，
∵OB＝OE，
∴OM∥ED，ED＝2OM，
∵OA∥ED，
∴△AOF∽△DEF，
∴，
∴11，
∴，
∵OA＝OB＝OE，
∴y11，
∵∠AMB＝∠BMC＝90°，∠ABE＝∠BAC＝∠DAC＝∠DBC，
∴tan∠BAC＝tan∠DBCtan∠ABE＝x，
设AM＝a，则BM＝ax，CM＝x•BM＝ax2，
∴AC＝AM+CM＝a+ax2，
∴OA，OM＝AM﹣OA＝a，
∴y11，
∴y关于x的函数表达式为y．
【点评】此题重点考查圆周角定理、垂径定理、平行线的判定与性质、角平分线的性质、三角形的中位线定理、勾股定理、相似三角形的判定与性质、锐角三角函数与解直角三角形等知识，此题综合性强，难度较大，属于考试压轴题．
17．（2023•义乌市校级模拟）如图1：以x轴的正半轴上一点O1为圆心作⊙O1，交x轴于C、D两点，交y轴于A、B两点，以O为圆心OA为半径的⊙O与x轴的负半轴交于G点．设⊙O1的弦AC的延长线交⊙O于F点，连结GF，AG，若AO＝4，（1）求证：△AGC∽△AFG；
（2）求出点O1的坐标；
（3）如图2，线段EA、EB（或它们的延长线）分别交⊙O于点M、N．问：当点E在（不含端点A、B）上运动时，线段MN的长度是否会发生变化？若不变，求出MN的长度；若变化，请说明理由．
【分析】（1）根据垂直的定义及等腰三角形的性质推圆周角定理∠AGC＝∠AFG，根据圆周角定理得出∠GAC＝∠FAG，根据相似三角形的判定定理即可得解；
（2）连接AD，根据相似三角形的性质及勾股定理求出AG＝4，CG＝2，则OC＝2，根据圆周角定理及直角三角形的性质推出△ACO∽△DAO，根据相似三角形的性质求出OD＝8，进而求出O1C＝5，O1O＝3，据此即可得解；
（3）当点E在上运动时，MN的长度不变；易得△EMN∽△EBA，进而连接AN，则AN⊥BE，∠ANE＝90°，csE，MN＝AB•csE＝8csE，分析可得结论．
【解答】（1）证明：∵OA⊥OG，
∴∠AOG＝90°，
∵OA＝OG，
∴∠AGC＝45°，
∵∠AFG∠AOG，
∴∠AFG＝45°，
∴∠AGC＝∠AFG，
又∠GAC＝∠FAG，
∴△AGC∽△AFG；
（2）解：如图，连接AD，
由（1）知，△AGC∽△AFG，
∴，
∵AF＝2GF，
∴AG＝2CG，
∵OA＝4，∠AOG＝90°，OA＝OG，
∴AG＝4，
∴CG＝2，
∴OC＝OG﹣CG＝2，
∵⊙O1交x轴于C、D两点，
∴CD是⊙O1的直径，
∴∠CAD＝90°，
∴∠CAO+∠DAO＝90°，
∵OA⊥OG，
∴∠ACO＝∠AOD＝90°，
∴∠CAO+∠ACO＝90°，
∴∠ACO＝∠DAO，
∴△ACO∽△DAO，
∴，
∴OA2＝OC×OD，
∵OA＝4，OC＝2，
∴OD＝8，
∴CD＝OC+OD＝10，
∴O1C＝5，
∴O1O＝O1C﹣OC＝3，
∴点O1的坐标为（3，0）；
（3）解：当点E在上运动时，MN的长度不变；
在△EMN和△EBA中，∠E＝∠E，∠EMN＝∠EBA，
∴△EMN∽△EBA．
∴，
即MNAB，
如图，连接AN，
∵AB为⊙O的直径，
∴∠ANB＝90°，
∴∠ANE＝90°，
∴csE，
∴MN＝AB×csE＝8csE，
当点E在上运动时，∠E的大小不变，8csE是常量，故MN的长度不变．
【点评】此题是圆的综合题，考查了圆周角定理、相似三角形的判定与性质、等腰三角形的性质、锐角三角函数等知识，熟练掌握圆周角定理、相似三角形的判定与性质并作出合理的辅助线是解题的关键．
18．（2023•衡水模拟）在一平面内，点D是⊙A上的点，连接AD，AB、BC、CD是三条定长线段，将四条线段按如图1顺次首尾相接，把AB固定，让AD绕点A从AB开始逆时针旋转角α（0°＜α＜360°）到某一位置时，BC，CD将会跟随到相应的位置，且点C始终保持在AB上方．
​
​（1）若点D在AB上方且AD∥BC时，求∠ABC的度数（用含α的式子表示）；
（2）当AD旋转到如图2位置时，连接AC，AC与OA交于点P，连接PD，若∠ACD+2∠CDP＝90°，请判断CD与⊙A的位置关系，并说明理由；
（3）若⊙A的半径为1，BC＝3，AB＝CD＝5，连接AC．
①当点D落在CA的延长线上时，求线段AD扫过的面积（参考数据：tan37°）；
②当点A与点C的距离最大时，求点D到AB的距离；
③当点D在AB上方，且BC⊥CD时，直接写出sin∠ABC的值．​
【分析】（1）利用平行线的性质求解；
（2）结论：CD是⊙A的切线．如图2中，延长CA交⊙A于点T，连接DT．证明AC⊥CD即可；
（3）①求出圆心角，利用弧长公式求解；
②如图3﹣2中，过点D作DH⊥AB于点H，过点C作CJ⊥AB于点J．当A，D，C共线时，A，C两点之间距离最大．设BJ＝y，则有62﹣（5+y）2＝32﹣y2，求出CJ，再利用平行线分线段成比例定理求解；
③如图3﹣3中，过点A作AT⊥CD于点T，过点A作AR⊥BC于点R，则四边形ARCT是矩形，设DT＝x，AT＝y．构建方程组求解即可．
【解答】解：（1）如图1中，当AD∥BC时，
∠A+∠B＝180°，
∴∠B＝180°﹣α；
（2）结论：CD是⊙A的切线．
理由：如图2中，延长CA交⊙A于点T，连接DT．
∵PT是直径，
∴∠TDP＝90°，
∴∠T+∠DPT＝90°，
∵∠DPT＝∠ACD+∠CDP，
∴∠ACD+∠CDP+∠T＝90°
∵∠ACD+2∠CDP＝90°，
∴∠T＝∠CDP，
∵AT＝AD，
∴∠T＝∠ADT，
∴∠CAD＝∠T+∠ADT＝2∠T＝2∠CDP，
∴∠ACD+∠CAD＝90°，
∴∠ADC＝90°，
∴AD⊥CD，
∵AD是半径，
∴CD是⊙A的切线；
（3）①如图3﹣1中
∵CD＝AB＝5，AD＝1，
∴AC＝CD﹣AD＝5﹣1＝4，
∵BC＝3，
∴AC2+BC2＝AB2，
∴∠C＝90°，
∴tan∠CAN，
∴∠CAB≈37°，
∴线段AD扫过的面积；
②如图3﹣2中，过点D作DH⊥AB于点H，过点C作CJ⊥AB于点J．
当A，D，C共线时，A，C两点之间距离最大．
设BJ＝y，则有62﹣（5+y）2＝32﹣y2，
解得y，
∴CJ，
∵DH∥CJ，
∴，
∴，
∴DH，
∴点D到AB的距离为；
③如图3﹣3中，过点A作AT⊥CD于点T，过点A作AR⊥BC于点R，则四边形ARCT是矩形，设DT＝x，AT＝y．
则有，
解得，
∴AR＝CT＝5，
∴sin∠ABC．
【点评】本题属于圆综合题，考查了切线的判定，弧长公式，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会利用参数构建方程或方程组解决问题．
19．（2023•海曙区一模）定义，若四边形的一条对角线平分这个四边形的面积，则称这个四边形为倍分四边形，这条对角线称为这个四边形的倍分线．如图①，在四边形ABCD中，若S△ABC＝S△ADC，则四边形ABCD为倍分四边形，AC为四边形ABCD的倍分线．
（1）判断：若是真命题请在括号内打√，若是假命题请在括号内打×．
①平行四边形是倍分四边形． √
②梯形是倍分四边形． ×
（2）如图①，倍分四边形ABCD中，AC是倍分线，若AC⊥AB，AB＝3，AD＝DC＝5，求BC；
（3）如图②，△ABC中BA＝BC，以BC为直径的⊙O分别交AB、AC于点N、M，已知四边形BCMN是倍分四边形．
①求sinC；
②连结BM，CN交于点D，取OC中点F，连结MF交NC于E（如图③），若OF＝3，求DE．
【分析】（1）①平行四边形的对角线平分平行四边形的面积，可判断①是真命题；
②梯形的对角线不平分梯形的面积，可判断②是假命题；
（2）过D作DE⊥AC于E，根据AC是四边形ABCD的倍分线，AC⊥AB，可得DE＝AB＝3，故AE4，AC＝2AE＝8，故BC；
（3）①连接BM，CN，OM，设CN交OM于H，由BA＝BC，得AM＝CM，故S△BCM＝S△BAM＞S△BNM，可知倍分四边形BCMN中，CN是倍分线，即S△BCN＝S△MCN，而∠ANC＝90°，AM＝CM，有MN＝AM＝CMAC，从而，知OM⊥CN，NH＝CH，设OH＝m，由S△BCN＝S△MCN，有MH＝BN＝2m，可得OC＝OM＝3m，BC＝2OC＝6m，根据勾股定理可得BM＝2m，即得sin∠ACB；
②连接OM交CN于H，作MF中点P，连接DP，由F为OC的中点，得OC＝2OF＝6，BC＝2OC＝12，BF＝9，则BM＝BC•sin∠ACB＝4，CM4，证明△BDN≌△MDH（AAS），得DM＝BDBM＝2，故CD6，而DP是△MBF的中位线，可得DPBF，DP∥BC，故△DPE∽△CFE，即得DECD6．
【解答】解：（1）①平行四边形的对角线平分平行四边形的面积，故平行四边形是倍分四边形，①是真命题；
故答案为：√；
②梯形的对角线不平分梯形的面积，故梯形不是倍分四边形，②是假命题；
故答案为：×；
（2）过D作DE⊥AC于E，如图：
∵AC是四边形ABCD的倍分线，AC⊥AB，
∴AB•ACDE•AC，
∴DE＝AB＝3，
在Rt△ADE中，
AE4，
∵AD＝DC，DE⊥AC，
∴AC＝2AE＝8，
在Rt△ABC中，
BC，
∴BC的长为；
（3）①连接BM，CN，OM，设CN交OM于H，如图：
∵BC为⊙O的直径，
∴∠BNC＝∠BMC＝90°，
∵BA＝BC，
∴AM＝CM，
∴S△BCM＝S△BAM＞S△BNM，
∴倍分四边形BCMN中，CN是倍分线，即S△BCN＝S△MCN，
∵∠ANC＝180°﹣∠BNC＝90°，AM＝CM，
∴MN＝AM＝CMAC，
∴，
∴OM⊥CN，NH＝CH，
设OH＝m，则BN＝2m，
∵S△BCN＝S△MCN，
∴BN•CNMH•CN，
∴MH＝BN＝2m，
∴OM＝OH+MH＝3m，
∴OC＝OM＝3m，BC＝2OC＝6m，
在Rt△OCH中，CH2＝OC2﹣OH2＝8m2，
在Rt△CMH中，CM2m，
在Rt△BMC中，BM2m，
∴sin∠ACB；
②连接OM交CN于H，作MF中点P，连接DP，如图：
∵F为OC的中点，
∴OC＝2OF＝6，BC＝2OC＝12，BF＝9，
在Rt△BCM中，BM＝BC•sin∠ACB＝124，
∴CM4，
由①知，BN＝MH，
∵∠BND＝∠MHD＝90°，∠BND＝∠MDH，
∴△BDN≌△MDH（AAS），
∴DM＝BDBM＝2，
∴CD6，
∵P为MF的中点，
∴DP是△MBF的中位线，
∴DPBF，DP∥BC，
∴△DPE∽△CFE，
∴，
∴DECD6．
【点评】本题考圆的综合应用，涉及新定义，全等三角形的判定与性质，相似三角形判定与性质，锐角三角函数，勾股定理等知识，解题的关键是作辅助线，构造直角三角形解决问题．
20．（2023•松江区二模）如图1，AB是半圆O的直径，C是半圆O上一点，点O′与点O关于直线AC对称，射线AO′交半圆O于点D，弦AC交O′O于点E、交OD于点F．
（1）如图2，O′恰好落在半圆O上，求证：；
（2）如果∠DAB＝30°，求的值：
（3）如果OA＝3，O'D＝1，求OF的长．
【分析】（1）连接OC，由点O′与点O关于直线AC对称得到AO＝AO′，证出△AOO′是等边三角形，得出∠AOO′＝∠BOC＝60°，即可得结论．
（2）设⊙O的半径为2a，作ON⊥AD于N，则OA＝O′A＝2a，求出AN，AD，ON，得到O′D，再求出OO′，得到OE，证出∠EFO＝45°，得到EF＝OE，作比即可．
（3）①当点O′在⊙O内部时，过点F作FN⊥AB于N，FM⊥AD于M，由，得到，又DF+OF＝OD，从而求得OF．②当点O′在⊙O外部时，同样方法求得OF的长．
【解答】（1）证明：如图2，连接OC，
∵点O′与点O关于直线AC对称，
∴OE＝O′E，AC⊥OO′，
∴AO＝AO′，，
∵AO＝OO′，
∴△AOO′是等边三角形，
∴∠AOO′＝60°，
∴∠COO′＝∠AOO′＝60°，
∴∠BOC＝60°，
∴∠AOO′＝∠BOC，
∴．
（2）解：如图3，设⊙O的半径为2a，
则OA＝O′A＝2a，
作ON⊥AD于N，
∵OA＝OD，∠DOB＝30°，
∴∠AOD＝120°，
在Rt△AON中，ON＝OA•sin30°＝a，
AN＝OA•cs30°a，
∵ON⊥AD，
∴AD＝2ANa，
∴O′D＝AD﹣O′A＝（）a，
∴O′N＝DN﹣O′D＝（2）a，
∴OO′（）a，
∵点O′与点O关于直线AC对称，
∴OE＝O′EOO′a，
由对称性得，∠BAC＝∠DAC＝15°，
∴∠EFO＝180°﹣∠BAC﹣∠AOD＝180°﹣15°﹣120°＝45°，
∴EF＝OEa，
∴．
（3）解：①如图4，当点O′在⊙O内部时，
AD＝O′A+O′D＝OA+O′D＝3+1＝4，
由对称性知∠DAF＝∠BAF，
过点F作FN⊥AB于N，FM⊥AD于M，
∴FM＝FN，
∴，
∴，
∵DF+OF＝OD＝3，
∴OF．
②如图5，当点O′在⊙O外部时，
过点F作FN⊥AB于N，FM⊥AD于M，
则FM＝FN，
∴，
∴，
又AD＝AO′﹣O′D＝OA﹣O′D＝3﹣1＝2，
∴，
∵DF+OF＝3，
∴OF．
综上得，OF或．
【点评】本题考查了圆周角定理、垂径定理、勾股定理、三角函数等知识，综合性较强，解答本题需要我们熟练各部分的内容，对学生的综合能力要求较高，一定要注意将所学知识贯穿起来．