中考数学二轮培优题型训练压轴题19以翻折旋转为背景的几何类比探究压轴问题（2份，原卷版+解析版）

这是一份中考数学二轮培优题型训练压轴题19以翻折旋转为背景的几何类比探究压轴问题（2份，原卷版+解析版），文件包含中考数学二轮培优题型训练压轴题19以翻折旋转为背景的几何类比探究压轴问题原卷版doc、中考数学二轮培优题型训练压轴题19以翻折旋转为背景的几何类比探究压轴问题解析版doc等2份试卷配套教学资源，其中试卷共79页， 欢迎下载使用。
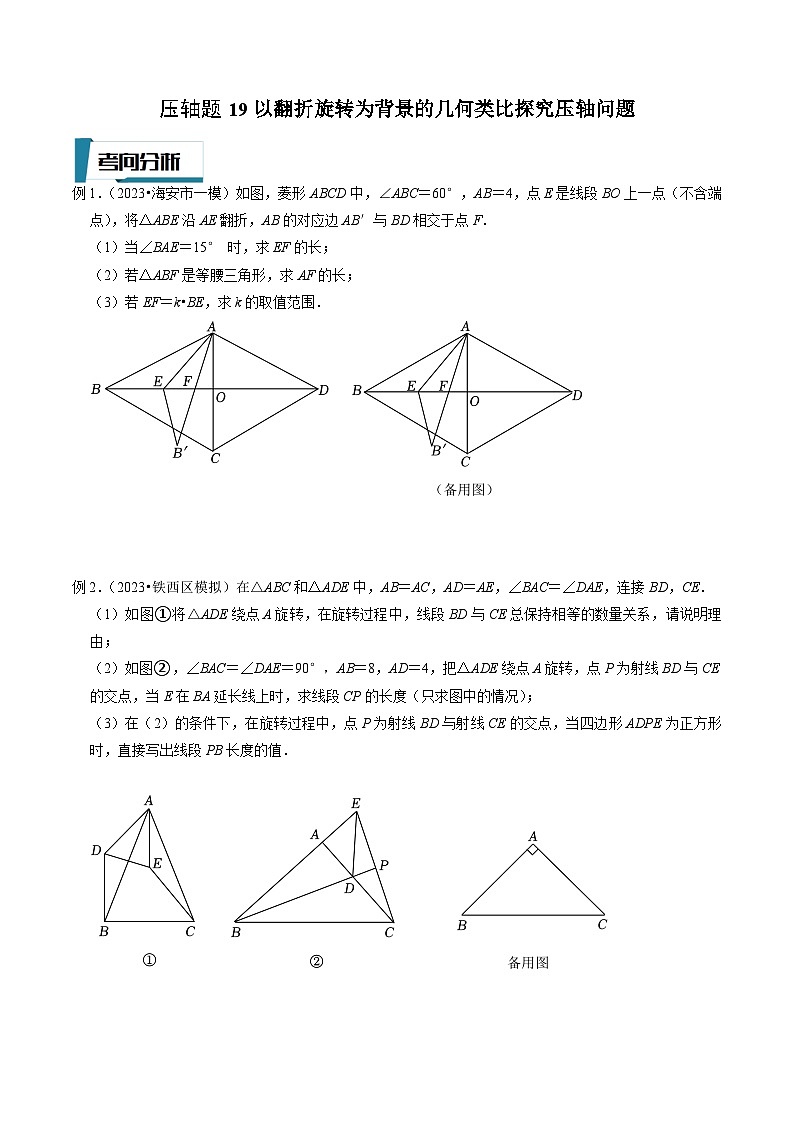
例1．（2023•海安市一模）如图，菱形ABCD中，∠ABC＝60°，AB＝4，点E是线段BO上一点（不含端点），将△ABE沿AE翻折，AB的对应边AB′与BD相交于点F．
（1）当∠BAE＝15° 时，求EF的长；
（2）若△ABF是等腰三角形，求AF的长；
（3）若EF＝k•BE，求k的取值范围．
​
例2．（2023•铁西区模拟）在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连接BD，CE．
（1）如图①将△ADE绕点A旋转，在旋转过程中，线段BD与CE总保持相等的数量关系，请说明理由；
（2）如图②，∠BAC＝∠DAE＝90°，AB＝8，AD＝4，把△ADE绕点A旋转，点P为射线BD与CE的交点，当E在BA延长线上时，求线段CP的长度（只求图中的情况）；
（3）在（2）的条件下，在旋转过程中，点P为射线BD与射线CE的交点，当四边形ADPE为正方形时，直接写出线段PB长度的值．
例3．（2023•南阳一模）在综合与实践课上，老师组织同学们以“矩形的折叠”为主题开展数学活动．
问题情景：在矩形ABCD中，点E为AD边上一动点，点F为BC边上一点，连接EF，将四边形CDEF沿EF折叠，点C、D分别落在点C'、D'处，设∠EFC＝α．
（1）如图1，若∠EFC＝75°，AD＝AB，点F为BC的中点，延长D'C'交AB于点P．则PC'与PB的数量关系是 ，写出图中一个30°的角： ；
（2）如图2，若点F为BC的中点，AD＝2AB，45°＜α＜90°，延长D'C'交AB于点P．求PC'与PB的数量关系，并说明理由；
（3）如图3，若AB＝3，AD＝6，BF＝1，连接C'E，当点E为AD的三等分点时，直接写出的值．
例4．（2023•沈河区校级模拟）如图1，四边形ABCD中，∠BCD＝90°，AC＝AD，AF⊥CD于点F，交BD于点E，∠ABD＝2∠BDC．
（1）判断线段AE与BC的关系，并说明理由；
（2）若∠BDC＝30°，求∠ACD的度数；
（3）如图2，在（2）的条件下，线段BD与AC交于点O，点G是△BCE内一点，∠CGE＝90°，GE＝3，将△CGE绕着点C逆时针旋转60°得△CMH，E点对应点为M，G点的对应点为H，且点O，G，H在一条直线上直接写出OG+OH的值．
1．（2023•襄都区校级一模）已知点M，N是直线l上自左向右的两点，且MN＝8，点P是MN的中点，点Q是直线l上一点（不与点M，N重合），直线m经过点Q，MA⊥直线m于点A，NB⊥直线m于点B，连接PA，PB．
（1）如图1，当点Q在点P，N之间时，求证：PA＝PB；
（2）如图2，当点Q在点N的右侧时，若PN＝2NQ，且∠AQM＝30°，求AB和AP的长度．
2．（2023•齐齐哈尔一模）综合与实践．
旋转是几何图形运动中的一种重要变换，通常与全等三角形等数学知识相结合来解决实际问题，某学校数学兴趣小组在研究三角形旋转的过程中，进行如下探究：如图1，△ABC和△DMN均为等腰直角三角形，∠BAC＝∠MDN＝90°，点D为BC中点，△DMN绕点D旋转，连接AM、CN．
观察猜想：（1）在△DMN旋转过程中，AM与CN的数量关系为 ；
实践发现：（2）当点M、N在△ABC内且C、M、N三点共线时，如图2，求证：；
拓展延伸：（3）当点M、N在△ABC外且C、M、N三点共线时，如图3，探究AM、CM、DM之间的数量关系是 ；
解决问题：（4）若△ABC中，，在△DMN旋转过程中，当且C、M、N三点共线时，DM＝ ．
3．（2023•长安区一模）问题提出：
（1）如图，在△ABC中，∠BAC＝90°，AO是它的一条中线，则∠COA与∠B的数量关系是：∠COA＝ ∠B；
（2）如图，在△ABC中，∠A＝60°，BC＝6，CG⊥AB于点G，BH⊥AC于点H，O为BC边上一点，且OG＝OB，连接GH，求GH的长；
问题解决：
（3）某次施工中，工人师傅需要画一个20°的角，但他手里只有一把带刻度的直角尺，工程监理给出了下面简易的作图方法：
①画线段OB＝15cm，再过它的中点C作m⊥OB；
②利用刻度尺在m上寻找点A，使得OA＝15cm，再过点A作l∥OB；
③利用刻度尺过点O作射线，将射线与AC和l的交点分别记为点F、E，调节刻度尺使FE＝□cm时（“□”内的数字被汗渍侵蚀无法看清），则∠EOB＝20°；
你认为监理给的方法可行吗？如果可行，请写出“□”内的数字，并说明理由；如果不可行，请给出可行的方案．
4．（2023•南关区校级模拟）如图，在△ABC中，，BC＝3，tanB＝3，点D为边BC的中点．动点P从点B出发，沿折线BA﹣AC向点C运动，在BA、AC上的速度分别为每秒个单位长度和每秒个单位长度．连结AD、PD，设点P的运动时间为t秒（t＞0）．
（1）线段AC的长为 ；
（2）用含t的代数式表示线段AP的长；
（3）当∠APD为钝角时，求t的取值范围；
（4）做点B关于直线PD的对称点B′，连结B′D，当B′D⊥BC时，直接写出t的值．
5．（2023•盐田区二模）操作：如图1，点E在矩形ABCD边CD上，沿AE折叠，点D恰落在BC边上D'处．再将图1对折，使点E与点A重合，得多边形AC′FBNM（图2），点C的对应点为点C′．
思考：若AB＝6，AD＝10．
（1）求图1中CE的长；
（2）求证：△AC'F≌△ECD'．
探究：若用一张纸进行上述操作，判断C'F与BF的数量关系，并说明理由．
6．（2023•白塔区校级一模）已知，在△ABC中，AB＝BC，∠ABC＝90°，点D在射线CB上，连接DA，将线段DA绕点D逆时针旋转 90° 后得到DE，过点E作EM⊥BC交直线BC于点M，连接AE，CE．
（1）如图①，若点D在线段CB上（且不与点C、点B重合）时，
求证：
①MC＝BD；
②∠ACE＝90°
（2）延长AD与直线CE相交于点N，
①当点D在线段CB上（且不与点C、点B重合）时，如图②所示，若AD平分∠BAC，，且 ，求线段NE的长；
②当点D在射线CB上（且不与点C、点B重合）时，若 时，直接写出 ．
7．（2023•天宁区校级模拟）在平面直角坐标系xOy中，点A（0，2），点B在x轴正半轴上，点C在第一象限内．
（1）如图1，OB＝4．
①若△ABC是以AC为斜边的直角三角形，且tan∠BAC＝2．请在图（1）中利用圆规、无刻度直尺作出点C的位置（不写作法，保留作图痕迹），写出点C的坐标： ；
②若△ABC是等边三角形．求点C的坐标；
（2）如图2，△ABC是等边三角形，点C在以P（3，6）为圆心，半径为r的圆上．若存在两个△ABC满足条件，求r的取值范围．
8．（2023•长春一模）如图，在Rt△ABC中，∠C＝90°，AB＝5，．点P从点A出发，以每秒2个单位长度的速度向终点B匀速运动，过点P作PD⊥AB交折线AC﹣CB于点D，连结BD，将△DBP绕点D逆时针旋转90°得到△DEF．设点P的运动时间为t（秒）．
（1）AC＝ ．
（2）用含t的代数式表示线段PD的长．
（3）当点E落在AB边上时，求t的值．
（4）当△DEF与△ABC重叠部分为三角形时，直接写出t的取值范围．
9．（2023•市中区一模）（1）①如图1，等腰△ABC（BC为底）与等腰△ADE（DE为底），∠BAC＝∠DAE，则BD与CE的数量关系为 ；
②如图2，矩形ABCD中，AB＝3，AD＝4，则sin∠DAC＝ ；
（2）如图3，在（1）②的条件下，点E在线段CD上运动，将AE绕点A顺时针旋转得到AF，使∠EAF＝∠DAC，连接CF．当AE＝3时，求CF的长度；
（3）如图4，矩形ABCD中，若AB＝2，AD＝6，点E在线段CD上运动，将AE绕点A顺时针旋转得到AF，旋转角等于∠BAC，连结CF，AE的中点为G，CF的中点为H，若GH，直接写出DE的长．
10．（2023•武汉模拟）问题提出：
如图，△ABC为等边三角形，D为CB的延长线上一点，∠DAE＝∠DEA，探究BD与EC的数量关系．
问题探究：
（1）现将问题特殊化，如图2，当E为AC的中点，DM⊥AC于点M，探究DB与EC的数量关系，说明理由；
（2）再探究一般情形，如图1，（1）中的结论还成立吗？
问题拓展：
（3）如图3，若AE＝nEC，AB与DE交于点F，直接写出tan∠DFB的值（用含n的式子表示）．
11．（2023•二道区校级模拟）如图，在Rt△ABC中，∠B＝90°，AB＝4，．点P从点A出发，以每秒4个单位长度的速度向终点B匀速运动，点Q为线段BP的中点．点D与点C在PQ的同侧，且∠DPQ＝90°，∠DQP＝∠C．设点P的运动时间为t（秒）．
（1）线段PQ的长为 （用含t的代数式表示）；
（2）当点D落在AC边上时，求PD的长；
（3）当△DPQ与△ABC重叠部分是轴对称图形时，求t的值；
（4）当点D到△ABC任意两边距离相等时，直接写出t的值．
12．（2023•惠水县一模）如图，平行四边形ABCD中，AB＝7，BC＝10．点P是BC边上的一点，连接AP，以AP为对称轴作△ABP的轴对称图形△AQP．
（1）动手操作
当点Q正好落在AD边上时，在图①中画出△ABP的轴对称图形△AQP，并判断四边形ABPQ的形状是 ；
（2）问题解决
如图②，当点P是线段BC中点，且CQ＝2时，求AP的长；
（3）拓展探究
如图③，当点P、Q、D在同一直线上，且∠PQC＝∠PQA时，求PQ的长．
13．（2023•青山湖区模拟）●问题发现
如图1，△ABC和△DEF都是等边三角形，边BC和EF在同一直线上，O是边BC的中点，BE＝CF，连接AD，则下列结论正确的是 ．（填序号即可）
①OE＝OF；
②AD＝BE；
③AD⊥BE；
④整个图形是轴对称图形．
●数学思考
将图1中的△DEF绕着点O旋转，△ABC不动，连接AD和BE，如图2，则AD和BE具有怎样的数量和位置关系？请给出证明过程；
●拓展应用
已知AB＝8cm，DE＝4cm，在图1中的△DEF绕着点O旋转的过程中，当BE⊥DF时，求线段AD的长度．#ZZA0
14．（2023•苏州一模）如图，△ABC是边长为3的等边三角形，D是AB上一动点，连接CD，以CD为边向CD的右侧作等边三角形CDE，连接AE．
（1）【尝试初探】
如图1，当点D在线段AB上运动时，AC，DE相交于点F，在运动过程中发现有两个三角形始终保持全等，请你找出这对全等三角形，并说明理由．
（2）【深入探究】
如图2，当点D在线段AB上运动时，延长ED，交CB的延长线于点H，随着D点位置的变化，H点的位置随之发生变化，当AD＝2BD时，求tan∠DHC的值．
（3）【拓展延伸】
如图3，当点D在BA的延长线上运动时，CD，AE相交于点F，设△ADF的面积为S1，△CEF的面积为S2，当S2＝4S1时，求BD的长．
15．（2023•海淀区模拟）在△ABC中，∠ACB＝90°，AC＝BC＝4，将线段CA绕点C逆时针旋转α角得到线段CD，连接AD，过点C作CE⊥AD于点E，连接BD交CA，CE于点F，G．
（1）当α＝60°时，如图1，依题意补全图形，直接写出∠BGC的大小；
（2）当α≠60°时，如图2，试判断线段BG与CE之间的数量关系，并证明你的结论；
（3）若F为AC的中点，直接写出AD的长．
16．（2023•郸城县一模）综合与实践：
在综合与实践课上，老师让同学们以“矩形纸片的折叠”为主题开展数学活动．
在矩形ABCD中，E为AB边上一点，F为AD边上一点，连接CE、CF，分别将△BCE和△CDF沿CE、CF翻折，点D、B的对应点分别为点G、H，且C、H、G三点共线．
（1）如图1，若F为AD边的中点，AB＝BC＝6，点G与点H重合，则∠ECF＝ °，BE＝ ；
（2）如图2，若F为AD的中点，CG平分∠ECF，，BC＝2，求∠ECF的度数及BE的长．
（3）AB＝5，AD＝3，若F为AD的三等分点，请直接写出BE的长．
17．（2023•翼城县一模）综合与实践
问题解决：
（1）已知在△ABC中，AC＝BC，∠ACB＝90°，四边形CDEF是正方形，H为BF所在的直线与AD的交点．如图1，当点F在AC上时，请判断BF和AD的关系，并说明理由．
问题探究：
（2）如图2，将正方形CDEF绕点C旋转，当点D在直线AC右侧时，求证：BH﹣AHCH；
问题拓展：
（3）将正方形CDEF绕点C旋转一周，当∠ADC＝45°时，若AC＝3，CD＝1，请直接写出线段AH的长．
18．（2023•临朐县一模）九年级一班同学在数学老师的指导下，以“等腰三角形的旋转”为主题，开展数学探究活动．
操作探究：
（1）如图1，△OAB为等腰三角形，OA＝OB，∠AOB＝60°，将△OAB绕点O旋转180°，得到△ODE，连接AE，F是AE的中点，连接OF，则∠BAE＝ °，OF与DE的数量关系是 ；
迁移探究：
（2）如图2，（1）中的其他条件不变，当△OAB绕点O逆时针旋转，点D正好落在∠AOB的角平分线上，得到△ODE，求出此时∠BAE的度数及OF与DE的数量关系；
拓展应用：
（3）如图3，在等腰三角形OAB中，OA＝OB＝4，∠AOB＝90°．将△OAB绕点O旋转，得到△ODE，连接AE，F是AE的中点，连接OF．当∠EAB＝15°时，请直接写出OF的长．
19．（2023•雁塔区校级模拟）问题探究：
（1）如图1，等腰直角△ABC，∠BAC＝90°，点D是△ABC内的一点，且AD＝CD，BD＝BA．过点D作AC的垂线l，以l为对称轴，作△ABD关于l的轴对称图形△CED，连接BE．求∠DBC的度数．
问题解决：
（2）如图2，有一个三角形空地ABC．经测量，AC＝500米，∠B＝45°，∠ACB＝30°，现要在△ABC的边AC右侧扩建三角形区域ADC，DH⊥AC，垂足为H，且满足∠ADC＝45°，．请利用所学知识，求四边形ABCD的面积．
20．（2022•沭阳县校级模拟）（1）如图1，已知正方形ABCD的边长为6，圆B的半径为3，点P是圆B上的一个动点，则PDPC的最小值为 ，PDPC的最大值为 ．
（2）如图2，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，求PDPC的最小值，以及PDPC的最大值．