中考数学二轮培优题型训练压轴题27选择压轴题（几何篇）（2份，原卷版+解析版）

这是一份中考数学二轮培优题型训练压轴题27选择压轴题（几何篇）（2份，原卷版+解析版），文件包含中考数学二轮培优题型训练压轴题27选择压轴题几何篇原卷版doc、中考数学二轮培优题型训练压轴题27选择压轴题几何篇解析版doc等2份试卷配套教学资源，其中试卷共56页， 欢迎下载使用。
1．（2023•朝阳区校级三模）如图，AB是⊙O的直径，将OB绕着点O逆时针旋转40°得到OC，P是⊙O上一点，且与点C在AB的异侧，连结PA、PC、AC，若PA＝PC，则∠PAB的大小是（ ）
A．20°B．35°C．40°D．70°
【答案】B
【分析】由圆周角定理求出∠P＝70°，由等腰三角形的性质求出∴∠PAC＝55°，由三角形外角的性质求出∠CAO＝20°，即可得到∠PAB＝∠PAC﹣∠CAO＝35°．
【详解】解：∵∠AOC+∠BOC＝180°，∠BOC＝40°，
∴∠AOC＝140°，
∴∠P∠AOC＝70°，
∵PA＝PC，
∴∠PAC＝∠PCA（180°﹣∠P）＝55°，
∵OA＝OC，
∴∠OAO＝∠ACO，
∵∠BOC＝∠OAO+∠ACO＝2∠CAO，
∴∠CAO∠BOC＝20°，
∴∠PAB＝∠PAC﹣∠CAO＝35°．
故选：B．
【点睛】本题考查圆周角定理，等腰三角形的性质，旋转的性质，关键是由圆周角定理，求出∠P的度数．
2．（2023•河北区二模）如图，在平面直角坐标系中，菱形OABC的顶点A在x轴上，且∠COA＝45°，OA＝4，则点B的坐标为（ ）
A．B．C．，2）D．
【答案】A
【分析】作BD⊥x轴于点D，由菱形的性质得AB∥OC，AB＝OA＝4，则∠BAD＝∠COA＝45°，可求得AD＝BD＝AB•sin45°＝2，所以OD＝4+2，则B（4+2，2），于是得到问题的答案．
【详解】解：作BD⊥x轴于点D，则∠ADB＝90°，
∵四边形OABC是菱形，∠COA＝45°，OA＝4，
∴AB∥OC，AB＝OA＝4，
∴∠BAD＝∠COA＝45°，
∴∠ABD＝∠BAD＝45°，
∴AD＝BD＝AB•sin45°＝42，
∴OD＝4+2，
∴点B的坐标为（4+2，2），
故选：A．
【点睛】此题重点考查图形与坐标、菱形的性质、等腰直角三角形的判定与性质、锐角三角函数与解直角三角形等知识，正确地作出所需要的辅助线是解题的关键．
3．（2023•奉贤区二模）如图，矩形ABCD中，AB＝1，∠ABD＝60°，点O在对角线BD上，圆O经过点C．如果矩形ABCD有2个顶点在圆O内，那么圆O的半径长r的取值范围是（ ）
A．0＜r≤1B．1＜rC．1＜r≤2D．r≤2
【答案】B
【分析】解直角三角形得到BD＝2AB＝2，AD，如图，当圆O的半径长r＝1时，A、B、C、D四个点都在圆O上，当圆O的半径长r时，A、B在圆内，C在圆上，D点在圆外，观察图形即可得到结论．
【详解】解：矩形ABCD中，AB＝1，∠ABD＝60°，
∴BD＝2AB＝2，AD，
∵矩形的对角线相等且平分，
∴当圆O的半径长r＝1时，A、B、C、D四个点都在圆O上，
当圆O的半径长r时，A、B在圆内，C在圆上，D点在圆外，
∴如果矩形ABCD有2个顶点在圆O内，那么圆O的半径长r的取值范围是1＜r，
故选：B．
【点睛】本题考查了点与圆的位置关系，矩形的性质，解直角三角形，正确的作出图形是解题的关键．
4．（2023•广灵县模拟）如图，在Rt△ABC中，∠C＝90°，BC＝3，AC＝6，点O，D，E是AB边上的点，以点O为圆心，DE长为直径的半圆O与AC相切于点M，与BC相切于点N，则图中阴影部分的面积为（ ）
A．5B．9﹣2πC．9﹣πD．5﹣π
【答案】D
【分析】连接ON，OM，根据切线的性质得到∠ONC＝∠OMC＝90°，根据正方形的性质得到ON＝OM＝CN＝CM，∠NOM＝90°，根据相似三角形的性质得到OM＝2，根据三角形和正方形以及扇形的面积公式即可得到结论．
【详解】解：连接ON，OM，∵半圆O与AC相切于点M，与BC相切于点N，
∴∠ONC＝∠OMC＝90°，
∵∠C＝90°，ON＝OM，
∴四边形CMON是正方形，
∴ON＝OM＝CN＝CM，∠NOM＝90°，
∴∠BON+∠AOM＝90°，
∵∠AMO＝∠C＝90°，
∴OM∥BC，
∴△AOM∽△ABC，
∴，
∴，
∴OM＝2，
∴图中阴影部分的面积2×2＝5﹣π，
故选：D．
【点睛】本题考查了切线的性质，扇形面积的计算，相似三角形的判定和性质，熟练掌握切线的性质是解题的关键．
5．（2023•普陀区二模）如图，△ABC中，∠BAC＝60°，BO、CO分别平分∠ABC、∠ACB，AO＝2，下面结论中不一定正确的是（ ）
A．∠BOC＝120°B．∠BAO＝30°
C．OB＝3D．点O到直线BC的距离是1
【答案】C
【分析】由角平分线的定义求出∠OBC+∠OCB（∠ABC+∠ACB）＝60°，由三角形内角和定理求出∠BOC的度数，由三角形内心的性质求出∠BAO的度数是30°，
OB的长在变化不一定等于3，由直角三角形的性质得到ON＝1，由角平分线的性质得到OM＝ON＝1，得到O到BC的距离是1．
【详解】解：作OM⊥BC于M，ON⊥AB于N，
∵BO、CO分别平分∠ABC、∠ACB，
∴∠OBC∠ABC，∠OCB∠ACB，
∴∠OBC+∠OCB（∠ABC+∠ACB）（180°﹣∠BAC）＝60°，
∴∠BOC＝180°﹣（∠OBC+∠OCB）＝120°，
故A正确；
∵BO、CO分别平分∠ABC，
∴O是△ABC的内心，
∴AO平分∠BAC，
∵∠BAC＝60°，
∴∠BAO∠BAC＝30°，
故B正确；
OB的长在变化不一定等于3，
故C不一定正确；
∵∠ANO＝90°，∠NAO＝30°，
∴ONAO2＝1，
∴OM＝ON＝1，
∴O到BC的距离是1，
故D正确．
故选：C．
【点睛】本题考查角平分线的性质，关键是掌握角平分线的性质．
6．（2023•瓯海区模拟）如图，四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH，连结DH并延长交AB于点K，若DF平分∠CDK，则（ ）
A．B．C．D．
【答案】C
【分析】过点K作KM⊥AH，设DE＝a，AE＝b，先证得∠KHA＝∠KAH，可得KH＝KA，再证△EHD∽△EDA，可得，即，解出，再证△HED∽△HMK，列比例式求解即可．
【详解】解：过点K作KM⊥AH，设DE＝a，AE＝b，
∵DF平分∠CDK，
∴∠CDF＝∠EDH，
∵四个全等的直角三角形拼成“赵爽弦图”，得到正方形ABCD与正方形EFGH，
∴∠CDF＝∠ABH，DE＝AH，∠DEA＝∠EHB，
∴DF∥HB，
∴∠EDH＝∠BHK，
∴∠KBH＝∠KHB，
∴KH＝KB，
∵∠AHB＝90°，
∴∠KBH+∠KAH＝90°，∠KHB+∠KHA＝90°，
∴∠KHA＝∠KAH，
∴KH＝KA，
∴，
∵∠HED＝∠DEA，∠HDE＝∠EAD，
∴△EHD∽△EDA，
∴，
即，
解得：，
∵DE∥KM，
∴△HED∽△HMK，
∴，
故选：C．
【点睛】本题是四边形综合题，考查了正方形的性质，相似三角形的判定和性质，解题的关键是学会添加常用辅助线，构造相似三角形解决问题，属于中考压轴题．
7．（2023•花溪区模拟）勾股定理是人类数学文化的一颗璀璨明珠，是用代数思想解决几何问题的最重要工具也是数形结合的组带之一，如图，秋千静止时，踏板离地的垂直高度BE＝1m，将它往前推6m至C处时（即水平距离CD＝6m），踏板离地的垂直高度CF＝4m，它的绳索始终拉直，则绳索AC的长是（ ）
A．B．C．6mD．
【答案】A
【分析】设绳索AC的长是xm，则AB＝xm，求出AD＝AB+BE﹣DE＝（x﹣3）m，然后在Rt△ACD中，由勾股定理得出方程，解方程即可．
【详解】解：设绳索AC的长是xm，则AB＝xm，
∵DE＝FC＝4m，BE＝1m，
∴AD＝AB+BE﹣DE＝x+1﹣4＝（x﹣3）m，
在Rt△ACD中，由勾股定理得：AC2＝AD2+CD2，
即x2＝（x﹣3）2+62，
解得：x，
即绳索AC的长是m，
故选：A．
【点睛】本题考查了勾股定理的应用，由勾股定理得出方程是解题的关键．
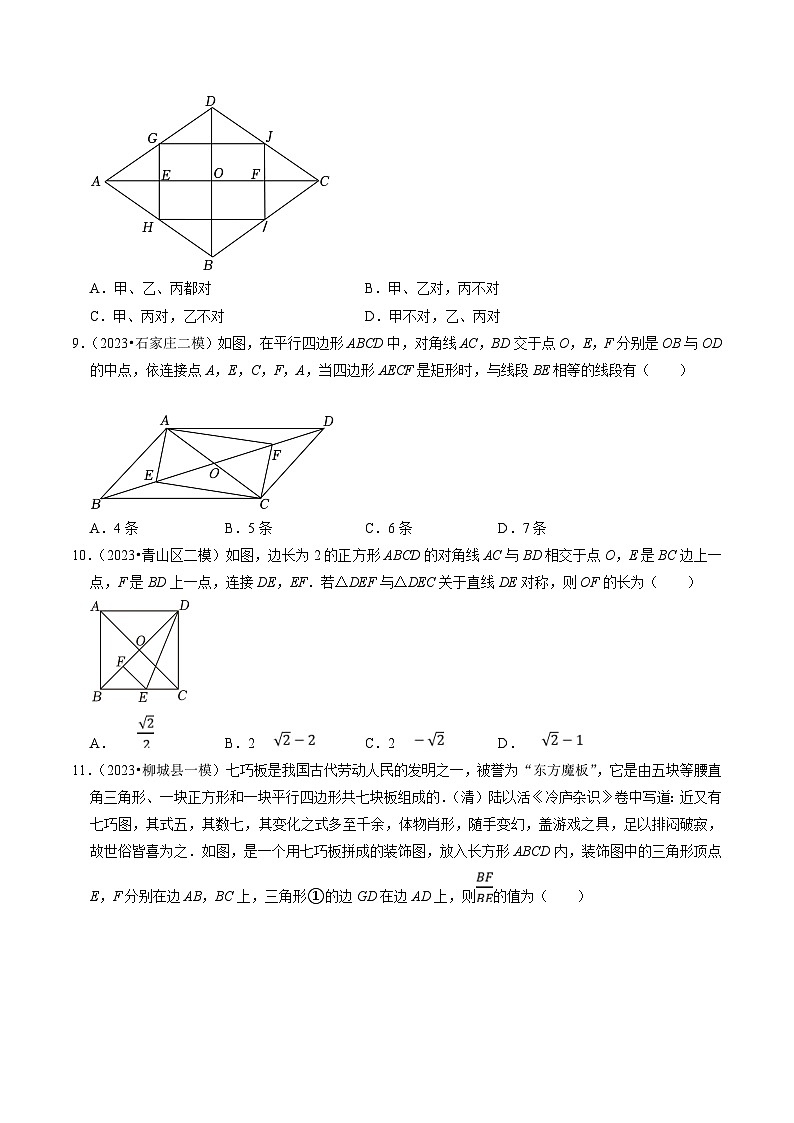
8．（2023•承德一模）如图，在菱形ABCD中，AC、BD（AC＞BD）相交于点O，E、F分别为OA和OC上的点（不与点A、O、C重合）．其中AE＝OF．过点E作GH⊥AC，分别交AD、AB于点G、H；过点F作IJ⊥AC分别交CD、CB于点J、I；连接GJ、HI，甲、乙、丙三个同学给出了三个结论：
甲：随着AE长度的变化，GH+IJ＝BD始终成立．
乙：随着AE长度的变化，四边形GHIJ可能为正方形．
丙：随着AE长度的变化，四边形GHIJ的面积始终不变，都是菱形ABCD面积的一半．
下列选项正确的是（ ）
A．甲、乙、丙都对B．甲、乙对，丙不对
C．甲、丙对，乙不对D．甲不对，乙、丙对
【答案】C
【分析】连接HJ，GI，交于点M，根据轴对称的性质得出GE＝EH，JF＝FI，MG＝MH，MJ＝MI，GJ＝HI，EO＝FC，过点G作GK⊥BD于点K，过点J作JT⊥BD于点T，证明△DTJ≌△GEA，△DKG≌△JFC得出GH+IJ＝BD，即可判断甲，进而得出四边形AHJD是平行四边形，四边形HJBC是平行四边形，即可判断丙，反证法证明四边形GHIJ不可能是正方形，即可求解．
【详解】解：如图所示，连接HJ，GI，交于点M，
∵四边形ABCD是菱形，GH⊥AC，IJ⊥AC，
∴GH∥JI，
根据菱形是轴对称图形，AC是GH，IJ，BD的垂直平分线，
∴GE＝EH，JF＝FI，MG＝MH，MJ＝MI，GJ＝HI，
∵AE＝OF，OA＝OC，
∴EO＝FC，
如图所示，过点G作GK⊥BD于点K，过点J作JT⊥BD于点T，
则四边形GEOK，TJFO是矩形，
∴，，
∵四边形ABCD是菱形，
∴∠DAO＝∠DCO，
∵GK∥AO，TJ∥OC，
∴∠DJT＝∠DCA＝∠GAE，∠DGK＝∠DAC＝∠JCF，
∴△DTJ≌△GEA（ASA），△DKG≌△JFC（ASA），
∴DJ＝AG，JC＝GD，GE＝DT，JF＝DK，
∴，
即GH+IJ＝BD，故甲正确，
∵DJ＝AG，又AG＝AH，
∴JD＝AH，
∴四边形AHJD是平行四边形，
∴，HJ∥AD，HJ＝AD，
∴四边形HJBC是平行四边形，
∴，
∴，
即四边形GHIJ的面积始终不变，都是菱形ABCD面积的一半，故丙正确；
同理可得四边形AGBI，CDGI是平行四边形，
∴GI∥CD，HJ∥AD，
∵当四边形GHIJ是正方形时，则GI⊥HJ，
∴AD⊥DC，
则四边形ABCD是正方形，
∵AC＞BD，
∴四边形ABCD不是正方形，即四边形GHIJ不可能是正方形，故乙错误，
故选：C．
【点睛】本题考查了平行四边形的性质与判定，菱形的性质，正方形的性质，熟练掌握以上知识是解题的关键．
9．（2023•石家庄二模）如图，在平行四边形ABCD中，对角线AC，BD交于点O，E，F分别是OB与OD的中点，依连接点A，E，C，F，A，当四边形AECF是矩形时，与线段BE相等的线段有（ ）
​
A．4条B．5条C．6条D．7条
【答案】B
【分析】由平行四边形的性质得OB＝OD，由E，F分别是OB与OD的中点，得OE＝BEOB，OF＝DFOD，则OE＝OF＝DF＝BE，由矩形的性质得，OA＝OCAC，OE＝OFEF且AC＝EF，OA＝OC＝OE＝OF＝DF＝BE，可知与线段BE相等的线段有5条，于是得到问题的答案．
【详解】解：∵四边形ABCD是平行四边形，对角线AC，BD交于点O，
∴OB＝OD，
∵E，F分别是OB与OD的中点，
∴OE＝BEOB，OF＝DFOD，
∴OE＝OF＝DF＝BE，
∵四边形AECF是矩形，
∴OA＝OCAC，OE＝OFEF，AC＝EF，
∴OA＝OC＝OE＝OF＝DF＝BE，
∴与线段BE相等的线段有5条，
故选：B．
【点睛】此题重点考查平行四边形的性质、矩形的性质、线段中点的定义等知识，证明OB＝OD、OA＝OC且AC＝EF是解题的关键．
10．（2023•青山区二模）如图，边长为2的正方形ABCD的对角线AC与BD相交于点O，E是BC边上一点，F是BD上一点，连接DE，EF．若△DEF与△DEC关于直线DE对称，则OF的长为（ ）
A．B．2C．2D．
【答案】C
【分析】根据正方形的性质和轴对称的性质得出DF＝DC和DBDC，进而解答即可．
【详解】解：∵四边形ABCD是正方形，DC＝2，
∴DBDC＝2，OD＝OB，
∴OD
∵△DEF与△DEC关于直线DE对称，
∴DF＝DC＝2，
∴OF＝DF﹣OD＝2，
故选：C．
【点睛】此题考查正方形的性质，关键是根据正方形的性质得出DB和OD解答．
11．（2023•柳城县一模）七巧板是我国古代劳动人民的发明之一，被誉为“东方魔板”，它是由五块等腰直角三角形、一块正方形和一块平行四边形共七块板组成的．（清）陆以活《冷庐杂识》卷中写道：近又有七巧图，其式五，其数七，其变化之式多至千余，体物肖形，随手变幻，盖游戏之具，足以排闷破寂，故世俗皆喜为之．如图，是一个用七巧板拼成的装饰图，放入长方形ABCD内，装饰图中的三角形顶点E，F分别在边AB，BC上，三角形①的边GD在边AD上，则的值为（ ）
A．B．C．D．
【答案】D
【分析】设七巧板正方形的边长为x，根据正方形的性质、矩形的性质分别表示出BF，BE的长，即可求解．
【详解】解：设七巧板正方形的边长为x，
∴2BE2＝x2，
∴BE2，
∴BEc，
∴，
∴，
故选：D．
【点睛】本题考查了矩形的性质，七巧板，勾股定理，正方形的性质，表示出BF，BE的长是解题的关键．
12．（2023•泉州模拟）如图，在矩形ABCD中，AB＝2，BC＝4，将△ABC沿BC的方向平移至△A'B'C'，使得A′E＝A′F，其中E是A′B′与AC的交点，F是A′C′与CD的交点，则CC′的长为（ ）
A．B．C．D．
【答案】C
【分析】由矩形的性质得AB∥CD，由平移得AB∥A′B′，AC∥A′C′，所以A′B′∥CD，而A′E＝A′F，即可证明四边形A′ECF是菱形，因为∠EB′C＝∠ABC＝90°，AB＝2，BC＝4，tan∠ACB，则B′C＝2EB′，由勾股定理得A′E＝CEEB′，则EB′EB′＝2，得EB′，所以B′C1，即可求得CC′＝BB′＝5，于是得到问题的答案．
【详解】解：∵四边形ABCD是矩形，
∴AB∥CD，
由平移得AB∥A′B′，AC∥A′C′，
∴A′B′∥CD，A′F∥CE，
∴A′E∥CF，
∴四边形A′ECF是平行四边形，
∵A′E＝A′F，
∴四边形A′ECF是菱形，
∵∠EB′C＝∠ABC＝90°，AB＝2，BC＝4，
∴tan∠ACB，
∴B′C＝2EB′，
∴A′E＝CEEB′，
∴EB′EB′＝A′B′＝AB＝2，
∴EB′，
∴B′C＝21，
∴CC′＝BB′＝BC﹣B′C＝4﹣（1）＝5，
故选：C．
【点睛】此题重点考查矩形的性质、平移的性质、平行四边形的判定、菱形的判定与性质、勾股定理、锐角三角函数与解直角三角形等知识，证明四边形A′ECF是菱形是解题的关键．
13．（2023•定远县二模）如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，点P为BC边上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长度的最小值为（ ）
A．3B．2.5C．2.4D．2
【答案】C
【分析】以PA，PC为邻边作平行四边形PAQC，由平行四边形的性质可知O是AC中点，PQ最短也就是PO最短，所以应该过O作BC的垂线P′O，然后根据△P′OC和△ABC相似，利用相似三角形的性质即可求出PQ的最小值．
【详解】解：∵∠BAC＝90°，AB＝3，BC＝5，
∴AC4，
∵四边形APCQ是平行四边形，
∴PO＝QO，CO＝AO，
∵PQ最短也就是PO最短，
∴过O作BC的垂线OP′，
∵∠ACB＝∠P′CO，∠CP′O＝∠CAB＝90°，
∴△CAB∽△CP′O，
∴，
∴，
∴OP′，
∴则PQ的最小值为2OP′＝2.4，
故选：C．
【点睛】本题考查了勾股定理的运用、平行四边形的性质、相似三角形的判定和性质以及垂线段最短的性质，解题的关键是作出高线构造出相似三角形．
14．（2023•烟台一模）如图，在矩形ABCD中，AB＝12，AD＝10，点E在AD上，点F在BC上，且AE＝CF，连结CE，DF，则CE+DF的最小值为（ ）
A．26B．25C．24D．22
【答案】A
【分析】先连接BE，将CE+DF转化为CE+BE，再利用将军饮马解决问题即可．
【详解】解：如图，连接BE，
∵四边形ABCD是矩形，
∴AB＝CD，∠BAE＝∠DCF＝90°，
∵AE＝CF，
∴△ABE≌△CDF，
∴BE＝DF，
∴CE+DF＝CE+BE，
如图，作点B关于A点的对称点B'，连接CB'，
CB'即为CE+BE的最小值，
∵AB＝12，AD＝10，
∴BB'＝24，BC＝10，
∴，
∴CE+DF的最小值为26，故A正确．
故选：A．
【点睛】本题考查矩形的性质、勾股定理、将军饮马问题、全等三角形的判定与性质等内容，综合性较强，将CE+DF转化为CE+BE是解题的关键．
15．（2023•郯城县一模）如图，在Rt△ABC中，∠BAC＝90°，AB＝6，BC＝10，点P为BC边上任意一点，连接PA，以PA，PC为邻边作平行四边形PAQC，连接PQ，则PQ长度的最小值为（ ）
A．4.8B．5C．2.4D．4
【答案】A
【分析】利用勾股定理得到BC边的长度，根据平行四边形的性质，得知OP最短即为PQ最短，利用垂线段最短得到点P的位置，再证明△CAB∽△CP'O利用对应线段的比得到OP'的长度，继而得到PQ的长度．
【详解】解：∵∠BAC＝90°，AB＝6，BC＝10，
∴，
∵四边形APCQ是平行四边形，
∴PO＝QO，CO＝AO，
∵PQ最短也就是PO最短，
∴过O作BC的垂线OP'，
∵∠ACB＝∠P'CO，∠CP'O＝∠CAB＝90°，
∴△CAB∽△CP'O，
∴，
∴，
∴，
∴则PQ的最小值为．
故选：A．
【点睛】本题考查了平行四边形性质和相似三角形的判定与性质，垂线段最短的知识，解答此题的关键是利用垂线段最短求解．
16．（2023•白云区一模）如图，正方形ABCD的面积为3，点E在边CD上，且CE＝1，∠ABE的平分线交AD于点F，点M，N分别是BE，BF的中点，则下列结论错误的是（ ）
A．FDMNB．△DEF是等腰直角三角形
C．BN＝1D．tan∠FBE
【答案】D
【分析】根据正方形ABCD的面积为3，可得正方形的边长为，根据正方形的性质可得∠A＝∠ABC＝∠C＝∠D＝90°，BC＝AB＝CD＝AD，根据tan∠CBE，可知∠CBE＝30°，根据tan∠ABF，可得AF＝CE＝1，可得DF＝DE，即可判断B选项；根据勾股定理和三角形中位线定理可判断A选项；求出BF的长，进一步可得BN的长，即可判断C选项；根据∠FBE＝30°，tan∠FBE，即可判断D选项．
【详解】解：∵正方形ABCD的面积为3，
∴正方形的边长为，
在正方形ABCD中，∠A＝∠ABC＝∠C＝∠D＝90°，BC＝AB＝CD＝AD，
∴tan∠CBE，
∴∠CBE＝30°，
∴∠ABE＝60°，
∵BF平分∠ABE，
∴∠ABF＝∠FBE＝30°，
∵tan∠ABF，AB，
∴AF＝1，
∴AF＝CE，
∴DF＝DE，
∵∠D＝90°，
∴△DEF是等腰直角三角形，
故B不符合题意；
根据勾股定理，得EFDF，
∵M，N分别是BE，BF的中点，
∴MN是△BEF的中位线，
∴MNEF，
∴MNDF，
即DFMN，
故A不符合题意；
在△ABF中，根据勾股定理，得BF2，
∴BN＝1，
故C不符合题意；
∵∠FBE＝30°，
∴tan∠FBE，
故D符合题意，
故选：D．
【点睛】本题考查了正方形的性质，三角形中位线定理，等腰直角三角形的判定，角平分线，勾股定理，解直角三角形等，本题综合性较强，熟练掌握这些知识是解题的关键．
17．（2023•九龙坡区校级模拟）如图，在正方形ABCD中，O为AC、BD的交点，△DCE为直角三角形，∠CED＝90°，，若CE•DE＝6，则正方形的面积为（ ）
A．20B．22C．24D．26
【答案】C
【分析】过点O作OM⊥CE交EC延长线于M，作ON⊥DE于N，判断出四边形OMEN是矩形，根据矩形的性质可得∠MON＝90°，再求出∠COM＝∠DON，根据正方形的性质可得OC＝OD，然后利用“角角边”证明△COM和△DON全等，根据全等三角形对应边相等可得OM＝ON，CM＝DN，然后判断出四边形OMEN是正方形，根据CE•DE＝6即可解决问题．
【详解】解：如图，过点O作OM⊥CE交EC延长线于M，作ON⊥DE于N，
∵∠CED＝90°，
∴四边形OMEN是矩形，
∴∠MON＝90°，
∵∠COM+∠DOM＝∠DON+∠DOM，
∴∠COM＝∠DON，
∵四边形ABCD是正方形，
∴OC＝OD，
在△COM和△DON中，
，
∴△COM≌△DON（AAS），
∴OM＝ON，CM＝DN，
∴四边形OMEN是正方形，
∵OE＝3，
∴2NE2＝OE2＝（3）2＝18，
∴NE＝ON＝3，
∵DE+CE＝DE+EM+MC＝DE+EM+DN＝EN+EM＝2EN＝6，
设DE＝a，CE＝b，
∴a+b＝6，
∵CE•DE＝6，
CD2＝a2+b2＝（a+b）2﹣2ab＝62﹣2×6＝24，
∴S正方形ABCD＝24．
故选：C．
【点睛】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，作辅助线构造出全等三角形是解题的关键，也是本题的难点．
18．（2023•杭州一模）如图，有两张矩形纸片ABCD和EFGH，AB＝EF＝2cm，BC＝FG＝8cm．把纸片ABCD交叉叠放在纸片EFGH上，使重叠部分为平行四边形，且B点D与点G重合，当两张纸片交叉所成的角α最小时，tanα等于（ ）
A．B．C．D．
【答案】B
【分析】由“ASA”可证△CDM≌△HDN，可证MD＝DN，即可证四边形DNKM是菱形，当点B与点E重合时，两张纸片交叉所成的角a最小，由勾股定理求出MD的长，即可得出答案．
【详解】解：如图，∵四边形ABCD和四边形EFGH是矩形，
∴∠ADC＝∠HDF＝90°，CD＝AB＝2cm，
∴∠CDM＝∠NDH，且CD＝DH，∠H＝∠C＝90°，
∴△CDM≌△HDN（ASA），
∴MD＝ND，且四边形DNKM是平行四边形，
∴四边形DNKM是菱形，
∴KM＝MD，
∵sinα＝sin∠DMC，
∴当点B与点E重合时，两张纸片交叉所成的角a最小，
设MD＝KM＝acm，则CM＝8﹣a（cm），
∵MD2＝CD2+MC2，
∴a2＝4+（8﹣a）2，
∴a（cm），
∴tanα＝tan∠DMC，
故选：B．
【点睛】本题考查了矩形的性质，菱形的判定，勾股定理，全等三角形的判定和性质以及三角函数定义等知识；求MD的长是本题的关键．
19．（2023•高明区二模）矩形ABCD和直角三角形EFG的位置如图所示，点A在EG上，点D在EF上，若∠2＝55°，则∠1等于（ ）
A．155°B．135°C．125°D．105°
【答案】C
【分析】由图形可知∠ADC＝90°＝∠GEF，即可得出∠EAD+∠ADE＝90°，∠2+∠ADE＝90°，从而求得∠DAE＝∠2＝55°，根据平角的定义即可求得∠1＝180°﹣∠DAE＝125°．
【详解】解：∵∠ADC＝90°＝∠GEF，
∴∠EAD+∠ADE＝90°，∠2+∠ADE＝90°，
∴∠DAE＝∠2＝55°，
∴∠1＝180°﹣∠DAE＝125°，
故选：C．
【点睛】本题考查了矩形的性质，直角三角形两锐角互余，平角的定义，证得∠DAE＝∠2＝55°是解题的关键．
20．（2023•余姚市一模）如图，由两个正三角形组成的菱形内放入标记为①，②，③，④的四种不同大小的小正三角形5个，其中编号①的有2个．设未被覆盖的浅色阴影部分的周长为C1，深色阴影部分的周长为C2，若要求出C1﹣C2的值，只需知道其中两个小正三角形的边长，则这两个小三角形的编号为（ ）
A．①②B．②③C．①③D．②④
【答案】C
【分析】设标记为①，②，③，④的小正方形的边长分别是m、n、x、y，表示出C1和C2，即可解决问题．
【详解】解：设标记为①，②，③，④的小正方形的边长分别是m、n、x、y，
由题意得：C1＝4x+m+2n＝2（x+n）+2x+m，
C2＝2y+4m＝2（y+m）+2m，
∵x+n＝y+m，
∴C1﹣C2＝2x﹣m，
∴只需知道编号是①③的两个小正三角形的边长，即可求出C1﹣C2的值．
故选：C．
【点睛】本题考查菱形的性质，等边三角形的性质，关键是由菱形、等边三角形的性质，用m、n、x、y表示出C1和C2．
21．（2023•衡水二模）如图，点P是正方形ABCD的边BC上一点，点M是对角线BD上一点，连接PM并延长交BA的延长线于点Q，交AD于点G，取PQ的中点N．连接AN．若AQ＝PC，有下面两个结论：①DM＝DG，②AN⊥BD，则这两个结论中，正确的是（ ）
A．①对B．②对C．①②都对D．①②都不对
【答案】B
【分析】延长AN交BD于H，在AB上取点K，使AK＝AQ，由正方形ABCD，可得AB＝BC，∠CBA＝90°，∠DBA＝45°，根据AQ＝PC，AK＝AQ，有BK＝PB，∠BKP＝45°，而AN是△QPK的中位线，知AN∥PK，故∠NAK＝∠PKB＝45°，即得∠AHB＝180°﹣∠NAK﹣∠DBA＝90°，AN⊥BD，②正确；因∠DGM＝∠AGQ＝90°﹣∠Q，∠DMG＝90°﹣∠HNM＝90°﹣∠ANQ，∠Q与∠ANQ不一定相等，可得∠DGM与∠DMG不一定相等，从而DM与DG不一定相等，①错误．
【详解】解：延长AN交BD于H，在AB上取点K，使AK＝AQ，如图：
∵正方形ABCD，
∴AB＝BC，∠CBA＝90°，∠DBA＝45°，
∵AQ＝PC，AK＝AQ，
∴PC＝AK，
∴AB﹣AK＝BC﹣PC，即BK＝PB，
∴△BPK是等腰直角三角形，
∴∠BKP＝45°，
∵N是PQ中点，AQ＝AK，
∴AN是△QPK的中位线，
∴AN∥PK，
∴∠NAK＝∠PKB＝45°，
∴∠AHB＝180°﹣∠NAK﹣∠DBA＝180°﹣45°﹣45°＝90°，
∴AN⊥BD，故②正确；
∵∠DGM＝∠AGQ＝90°﹣∠Q，∠DMG＝90°﹣∠HNM＝90°﹣∠ANQ，
而∠Q与∠ANQ不一定相等，
∴∠DGM与∠DMG不一定相等，
∴DM与DG不一定相等，故①错误；
故选：B．
【点睛】本题考查正方形性质及应用，涉及等腰直角三角形判定与性质，三角形中位线定理等知识，解题的关键是作辅助线，构造等腰直角三角形解决问题．
22．（2023•新乡二模）如图，在矩形ABCD中，点B（0，4），点C（2，0），BC＝2CD，先将矩形ABCD沿y轴向下平移至点B与点O重合，再将平移后的矩形ABCD绕点O逆时针旋转90°得到矩形EOMN，则点D的对应点N的坐标为（ ）
A．（3，3）B．（4，4）C．（3，4）D．（4，3）
【答案】C
【分析】过点D作DF⊥x轴于点F，如图所示，先证明△BOC∽△CFD，得到，进而求出FC＝2，FD＝1，则点D（4，1）．由题意知矩形ABCD向下平移了4个单位长度，将点D向下平移4个单位长度到点D'（4，﹣3），连接OD'，DD'，则点F在线段DD'上，过点N作NP⊥x轴于点P，连接ON，如图所示证明△OD'F≌△NOP．得到OP＝D'F＝3，NP＝OF＝4，则点N的坐标为（3，4）．
【详解】解：过点D作DF⊥x轴于点F，如图所示，
由题意得，∠BOC＝∠BCD＝∠CFD＝90°，
∴∠OCB+∠OBC＝90°＝∠FCD+∠OBC，
∴∠OBC＝∠FCD，
∴△BOC∽△CFD，
∵BC＝2CD，
∴．
∵B（0，4），C（2，0），
∴OB＝4，OC＝2，
∴FC＝2，FD＝1．
∴点D（4，1）．
由题意知矩形ABCD向下平移了4个单位长度，将点D向下平移4个单位长度到点D'（4，﹣3），
连接OD'，DD'，则点F在线段DD'上，过点N作NP⊥x轴于点P，连接ON，如图所示．
由旋转的性质可得∠D'ON＝90°，OD′＝ON．
又∵∠D'FO＝∠OPN＝90°，
∴∠D'OF+∠NOP＝90°＝∠D′OF+∠OD'F．
∴∠OD'F＝∠NOP．
∴△OD'F≌△NOP（AAS）．
∴OP＝D'F＝3，NP＝OF＝4．
∴点N的坐标为（3，4），
故选C．
【点睛】本题主要考查了矩形的性质，平移的性质，旋转的性质，相似三角形的判定与性质，全等三角形的判定与性质，坐标与图形，等等，正确作出辅助线构造相似三角形和全等三角形是解题的关键．
23．（2023•荆门一模）如图，菱形ABCD各边的中点分别是E、F、G、H，若EH＝2EF，则下列结论错误的是（ ）
A．EH⊥EFB．EH＝ACC．∠B＝60°D．
【答案】C
【分析】由中位线的性质可知AC＝2EF，结合EH＝2EF可得EH＝AC，可判断B选项；由菱形的性质可知AC⊥BD，用勾股定理解Rt△AOB可验证选项D；先证四边形AHFB是平行四边形，再用勾股定理的逆定理证明△FEH是直角三角形，可判断选项A；假设∠B＝60°成立，则△FEB是等边三角形，，与矛盾，可判断选项C．
【详解】解：如图，连接AC，BD交于点O，连接FH，
∵菱形ABCD各边的中点分别是E、F、G、H，
∴，，
∴AC＝2EF，BD＝2EH，
∵EH＝2EF，
∴EH＝AC，
故B选项结论正确，不合题意；
由菱形的性质可知AC⊥BD，
∴OA2+OB2＝AB2，
∵，，
∴AB2＝EF2+EH2＝EF2+4EF2＝5EF2，
∴，
故D选项结论正确，不合题意；
∵，，AD＝BC，
∴AH＝BF，
又AH∥BF，
∴四边形AHFB是平行四边形，
∴AB＝HF，
∴EF2+EH2＝AB2＝HF2，
∴△FEH是直角三角形，
∴EH⊥EF，
故A选项结论正确，不合题意；
由已知条件可知BE＝BF，
若∠B＝60°，则△FEB是等边三角形，
则，与矛盾，
因此∠B＝60°不成立，
故C选项结论错误，符合题意．
故选：C．
【点睛】本题考查菱形的性质，勾股定理及其逆定理，三角形中位线的性质，平行四边形的判定与性质等，解题的关键是综合运用上述知识点，逐步进行推导论证．
24．（2023•中原区校级二模）如图，在Rt△ABO中，AB＝OB，顶点A的坐标为（2，0），以AB为边向△ABO的外侧作正方形ABCD，将组成的图形绕点O逆时针旋转，每次旋转45°，则第98次旋转结束时，点D的坐标为（ ）
A．（1，﹣3）B．（﹣1，3）C．（﹣1，2）D．（1，3）
【答案】B
【分析】过D作DH⊥x轴于H，由在Rt△ABO中，AB＝OB，OA＝2，得AB，∠BAO＝45°，根据四边形ABCD是正方形，可得D（3，1），又将组成的图形绕点O逆时针旋转，每次旋转45°，知每旋转8次回到初始位置，第98次旋转结束，相当于将D（3，1）旋转90°，即可得到答案．
【详解】解：过D作DH⊥x轴于H，如图：
∵在Rt△ABO中，AB＝OB，OA＝2，
∴AB，∠BAO＝45°，
∵四边形ABCD是正方形，
∴AD＝AB，∠BAD＝90°，
∴∠DAH＝45°，
∴△ADH是等腰直角三角形，
∴AH＝DH1，
∴OH＝OA+AH＝3，
∴D（3，1），
∵将组成的图形绕点O逆时针旋转，每次旋转45°，
∴每旋转8次回到初始位置，
∵98÷8＝，
∴第98次旋转结束，相当于将D（3，1）旋转90°，
∴第98次旋转结束时，点D的坐标为（﹣1，3），
故选：B．
【点睛】本题考查正方形的性质及应用，涉及旋转变换，解题的关键是掌握正方形的性质，找到旋转的规律．
25．（2023•中原区模拟）如图，▱ABCD的边BC在x轴的负半轴上，点B与原点O重合，DE⊥AB，交BA的延长线于点E，已知∠ABC＝60°，AB＝4，BC＝6，则点E的坐标为（ ）
A．（﹣2，﹣，2）B．（﹣3，3）C．（，）D．（，）
【答案】C
【分析】过点E作EF⊥y轴于点F，由平行四边形的性质得AD＝BC＝6，AD∥BC，再由含30°角的直角三角形的性质得AE＝3，EF，然后由勾股定理得OF，即可得出结论．
【详解】解：如图，过点E作EF⊥y轴于点F，
则∠EFO＝90°，
∵四边形ABCD是平行四边形，
∴AD＝BC＝6，AD∥BC，
∴∠EAD＝∠ABC＝60°，
∵DE⊥AB，
∴∠AED＝90°，
∴∠ADE＝90°﹣∠EAD＝30°，
∴AEAD＝3，
∴BE＝AB+AE＝4+3＝7，
∵∠EOF＝90°﹣∠ABC＝30°，
∴EFOE，
∴OF，
∴点E的坐标为（，），
故选：C．
【点睛】本题考查了平行四边形的性质、坐标与推出性质、含30°角的直角三角形的性质以及勾股定理等知识，熟练掌握平行四边形的性质和含30°角的直角三角形的性质是解题的关键．
26．（2023•武邑县二模）如图，N是正六边形ABCDEF对角线CF上一点，延长FE，CD相交于点M，若S△ABN＝2，则S五边形ABCMF＝（ ）
A．10B．12C．14D．16
【答案】C
【分析】根据正六边形的性质得出S△ABN＝S△AOBS正六边形ABCDEF＝S△DEM即可．
【详解】解：如图，正六边形的中心为O，则点O在CF上，由正六边形的性质可知，
AB∥CF，
∴S△ABN＝S△AOBS正六边形ABCDEF＝2＝S△DEM，
∴S五边形ABCMF＝7S△AOB
＝14，
故选：C．
【点睛】本题考查正六边形和圆，三角形面积的计算，掌握正六边形的性质以及三角形、正六边形面积的计算方法是正确解答的前提．
27．（2023•承德一模）如图，正六边形的两条对角线AE、BE把它分成Ⅰ、Ⅱ、Ⅲ三部分，则该三部分的面积比为（ ）
A．1：2：3B．2：2：4C．1：2：4D．2：3：5
【答案】A
【分析】根据正多边形的性质，三角形中线的性质即可求解．
【详解】解：如图，连接AD，CF交BE于点O，CF，AE交于点P，
∵正六边形，
∴△AOF≌△EOF≌△DOE≌△DOC≌BOC≌AOB（SSS），
∵△AEF和△AEO是等腰三角形，FO分别是∠AFE和∠AOE的角分线，
∴FO⊥AE，AP＝EP（三线合一），
∴Rt△APF≌Rt△EPF≌Rt△EPO≌Rt△APO（HL），
∴S△AEF＝S△AOES四边形AOEF＝S△AOF，
∴S△AFE＝S△AOE＝S△AOB＝S△COB＝S△COD＝S△DOE，
∴Ⅰ、Ⅱ、Ⅲ三部分的面积比为1：2：3，
故选：A．
【点睛】本题考查了正多边形，三角形中线的性质，熟记图形的性质并准确识图是解题的关键．
28．（2023•罗湖区二模）如图，AB为圆O的直径，C为圆O上一点，过点C作圆O的切线交AB的延长线于点D，，连接AC，若AB＝8，则AC的长度为（ ）
A．B．C．D．
【答案】C
【分析】根据，AB为圆O的直径可得OA＝OB＝DB，结合DC是圆O的切线即可得到∠OCD＝90°，即可得到CB＝OB，根据勾股定理即可得到答案．
【详解】解：连接OC，BC，
∵，AB为圆O的直径，
∴OA＝OB＝DB，∠ACB＝90°，
∵DC是圆O的切线，
∴∠OCD＝90°，
∵OB＝DB，
∴CB＝OB，
∵AB＝8，
∴BC＝4，
在Rt△ABC中，，
故选：C．
【点睛】本题考查圆周角定理，勾股定理，直角三角形斜边上的中线等于斜边一半，解题的关键是求出BC．
29．（2023•杭州一模）如图，过⊙O外一点A作⊙O的切线AD，点D是切点，连结OA交⊙O于点B，点C是⊙O上不与点B，D重合的点．若∠A＝α°，则∠C的度数为（ ）
A．B．C．2α°D．
【答案】A
【分析】由切线的性质定理，得到∠ADO＝90°，由直角三角形的性质得到，∠AOD＝90°﹣α°，由圆周角定理得到∠C∠AOD＝（45α）°．
【详解】解：∵AD切圆于D，
∴半径OD⊥AD，
∴∠ADO＝90°，
∵∠A＝α°，
∴∠AOD＝90°﹣α°，
∴∠C∠AOD＝（45α）°．
故选：A．
【点睛】本题考查切线的性质，圆周角定理，关键是掌握切线的性质定理，圆周角定理．
30．（2023•西宁一模）如图，扇形纸片AOB的半径为3，沿AB所在直线折叠扇形纸片，圆心D恰好落在上的点C处，则阴影部分的面积是（ ）
A．B．C．D．
【答案】A
【分析】根据折叠变换的性质得到AC＝AO，BC＝BO，推出四边形AOBC是菱形，连接OC交AB于D，根据等边三角形的性质得到∠CAO＝∠AOC＝60°，求得∠AOB＝120°，根据菱形和扇形的面积公式即可得到结论．
【详解】解：沿AB折叠扇形纸片，点O恰好落在上的点C处，
∴AC＝AO，BC＝BO，
∵AO＝BO，
∴四边形AOBC是菱形，
连接OC交AB于D，
∵OC＝OA，
∴△AOC是等边三角形，
∴∠CAO＝∠AOC＝60°，
∴∠AOB＝120°，
∵AC＝3，
∴OC＝3，ADAC，
∴AB＝2AD＝3，
∴图中阴影部分的面积＝S扇形AOB﹣S菱形AOBC3×33π，
故选：A．
【点睛】本题考查了扇形面积的计算，菱形的判定和性质，等边三角形的判定和性质，正确地作出辅助线是解题的关键．
31．（2023•太原一模）如图，在扇形纸片OAB中，∠AOB＝105°，OA＝6、点C是半径OA上的点、沿直线BC折叠△OBC得到△DBC，点O的对应点D落在上，图中阴影部分的面积为（ ）
A．B．C．9π﹣18D．12π﹣18
【答案】B
【分析】连接OD，根据折叠性质可知△BOD等边三角形，然后再求出S扇形OAD、S△COD，即可求解．
【详解】解：如图，连接OD，
由折叠的性质可得，BC⊥OD，OD＝OB＝BD，
∴△OBD是等边三角形，
∴∠BOD＝60°，
∵∠AOB＝105°，
∴∠COD＝45°．
∵CD＝CO，
∴∠CDO＝∠COD＝45°，
∴∠DCO＝90°，
∴CD＝ODOD＝3，
∴S扇形OADπ，S△COD•OC•CD339，
∴S阴影π﹣9．
故选：B．
【点睛】本题是扇形面积的综合练习题，考查了折叠的性质，以及扇形面积的公式，灵活运用即可．
32．（2023•西山区校级模拟）如图，分别以等边△ABC的三个顶点为圆心，边长为半径画弧，得到的封闭图形是莱洛三角形，若AB为6，则图中阴影部分的面积为（ ）
A．B．C．D．
【答案】D
【分析】图中三角形的面积是由三块相同的扇形叠加而成，其面积＝三块扇形的面积相加，再减去两个等边三角形的面积，分别求出即可．
【详解】解：过A作AD⊥BC于D，
∵△ABC是等边三角形，
∴AB＝AC＝BC＝6，∠BAC＝∠ABC＝∠ACB＝60°，
∵AD⊥BC，
∴BD＝CD＝3，ADBD＝3，
∴S△ABCBC•AD＝9，
S扇形BAC6π，
∴莱洛三角形的面积S＝3×6π﹣2×918π﹣18，
故选：D．
【点睛】本题考查了等边三角形的性质和扇形的面积计算，能根据图形得出莱洛三角形的面积＝三块扇形的面积相加、再减去两个等边三角形的面积是解此题的关键．
33．（2023•莆田模拟）如图，在⊙O中，∠AOB＝120°，点C在上，连接AC，BC，过点B作BD⊥AC的延长线于点D，当点C从点A运动到点B的过程中，∠CBD的度数（ ）
A．先增大后减小B．先减小后增大
C．保持不变D．一直减小
【答案】C
【分析】根据圆内接四边形的性质以及圆周角定理，三角形内角和定理进行计算即可．
【详解】解：如图，在优弧AB上任取一点E，连接AE，BE，
∵四边形AEBC是⊙O的内接四边形，
∴∠BCD＝∠AEB∠AOB＝60°，
∵BD⊥AD，
∴∠BDC＝90°，
∴∠BCD+∠CBD＝90°，
∴∠CBD＝90°﹣∠BCD＝30°，
因此∠CBD的大小不变，
故选：C．
【点睛】本题考查圆周角定理，圆内接四边形的性质以及三角形内角和定理，掌握圆周角定理、三角形内角和定理是正确解答的前提．
34．（2023•蚌埠二模）如图是某芯片公司的图标示意图，其设计灵感源于传统照相机快门的机械结构，圆O中的阴影部分是一个正六边形，其中心与圆心O重合，且AB＝BC，则阴影部分面积与圆的面积之比为（ ）
A．B．C．D．
【答案】B
【分析】根据题意，设正六边形的边长为1，进而求出圆的面积以及圆的内接正六边形面积，进一步计算可得答案．
【详解】解：如图所示，连接OA，OB，OC，
设正六边形的边长为1，则OA＝1，∠AOB＝60°，OA＝OB，
∴△AOB为等边三角形，则∠BOA＝∠OBA＝60°，OA＝OB＝AB＝1，AC＝2，
∴∠BCO＝∠BOC，
又∵∠ABO＝∠BCO+∠BOC，
∴∠BCO＝∠BOC＝30°，则∠AOC＝90°，
∴，即圆的半径为，
所以圆的面积为3π，正六边形的面积为6S△AOB＝6AB•OA•sin60°＝61×1，
则阴影部分面积与圆的面积之比为，
故选：B．
【点睛】本题考查了圆面积的计算，正六边形的性质，正确作出辅助线和正确的识别图形是解题的关键．
35．（2023•鄞州区校级模拟）如图，AB为⊙O的直径，将弧BC沿BC翻折，翻折后的弧交AB于D．若BC＝4，sin∠ABC，则图中阴影部分的面积为（ ）
​
A．B．C．8D．10
【答案】C
【分析】连接AC，CD，过点C作CH⊥AB于H．根据圆周角定理得出，则AC＝CD，从而得出S阴影＝S△ACD，解直角三角形求得CH、AD，利用三角形面积公式即可求得阴影的面积．
【详解】解：如图，连接AC，CD，过点C作CH⊥AB于H，
∵∠ABC＝∠DBC，
∴，
∴AC＝CD，
∵CH⊥AD，
∴AH＝HD，
∵BC＝4，sin∠ABC，
∴CH＝BC•sin∠ABC＝4，
∵AB为⊙O的直径，
∴∠ACB＝90°，
∵sin∠ABC，
∴设ACm，AB＝5m，
根据勾股定理，AC2+BC2＝AB2，
∴5m2+80＝25m2，
∴m＝2，
∴AC＝CD＝2，
∴AH2，
∴AD＝2AH＝4，
∴S阴影＝S△ACDAD•CH4×4＝8，
故选：C．
【点睛】本题考查扇形的面积，等腰三角形的判定和性质，解直角三角形，圆周角定理等知识，解题的关键是学会添加常用辅助线，构建直角三角形．
36．（2023•九龙坡区模拟）如图，在⊙O中，AB是圆的直径，过点B作⊙O的切线BC，连接AC交⊙O于点D，点E为弧AD中点，连接AE，若AE＝AO，AB＝6，则CD的长为（ ）
A．2B．C．D．
【答案】C
【分析】连接OE，OD，BD，由AE＝AO，AO＝OE，得到△AOE是等边三角形，因此∠AOE＝60°，由点E为弧AD中点，得到∠DOE＝∠AOE＝60°，由平角定义求出∠BOD＝60°，由圆周角定理求出∠BAC＝30°，由切线的性质定理得到∠ABC＝90°，即可求出CB的长，从而得到CDBC．
【详解】解：连接OE，OD，BD，
∵AE＝AO，AO＝OE，
∴△AOE是等边三角形，
∴∠AOE＝60°，
∵点E为弧AD中点，
∴∠DOE＝∠AOE＝60°，
∴∠BOD＝180°﹣∠AOE﹣∠DOE＝60°，
∴∠BAC∠BOD＝30°，
∵CB切圆于B，
∴直径AB⊥BC，
∴∠ABC＝90°，
∴BCAB6＝2，
∵AB是圆的直径，
∴∠ADB＝90°，
∵∠ABD∠AOD＝60°，
∴∠CBD＝90°﹣∠ABD＝30°，
∴CDBC．
故选：C．
【点睛】本题考查切线的性质，圆周角定理，圆心角、弧、弦的关系，直角三角形的性质，熟练掌握以上知识点是解题的关键．
37．（2023•宁德模拟）“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形．如图，以等边三角形ABC的三个顶点为圆心，以边长为半径画弧，三段圆弧围成的图形就是“莱洛三角形”．若等边三角形ABC的边长为2，则该“莱洛三角形”的周长等于（ ）
A．2πB．C．D．
【答案】A
【分析】由弧长公式：l（弧长为l，圆心角度数为n，圆的半径为r），求出的长，即可解决问题．
【详解】解：∵△ABC是等边三角形，
∴AB＝BC＝CA，∠BAC＝∠ABC＝∠BCA＝60°，
∴，
∵的长π，
∴“莱洛三角形”的周长等于的长×33＝2π．
故选：A．
【点睛】本题考查弧长的计算，等边三角形的性质，关键是掌握弧长公式．
38．（2023•虹口区二模）如图，在矩形ABCD中，对角线AC与BD相交于点O，AB＝5，BC＝12．分别以点O、D为圆心画圆，如果⊙O与直线AD相交、与直线CD相离，且⊙D与⊙O内切，那么⊙D的半径长r的取值范围是（ ）
A．B．C．D．9＜r＜13
【答案】C
【分析】设⊙O的半径是r′，由⊙O与直线AD相交、与直线CD相离，得到2.5＜r′＜6；两圆的圆心距是d、半径是R和r，两圆内切⇔d＝R﹣r（R＞r），由此即可求出⊙D的半径长的取值范围．
【详解】解：作OM⊥AD于M，ON⊥DC于N，
∵四边形ABCD是矩形，
∴BO＝OD＝OA＝OC，
∴MA＝MD，
∴OM是△DAB的中位线，
∴OMAB5＝2.5
同理：ONBC12＝6，
设⊙O的半径是r′，
∵⊙O与直线AD相交、与直线CD相离，
∴2.5＜r′＜6，
由题意知r＞r′，不然⊙D和⊙O不能内切，
∵BD13，
∴ODBD＝6.5，
∴两圆的圆心距d＝OD＝6.5，
∴d＝r﹣r'，
∴r＝6.5+r'，
∴2.5+6.5＜r＜6+6.5，
∴9＜r＜12.5．
故选：C．
【点睛】本题考查圆与圆的位置关系，矩形的性质，关键是掌握圆与圆的位置关系的判定方法．
39．（2023•苏州一模）东南环立交是苏州中心城区城市快速内环道路系统的重要节点，也是江苏省最大规模的城市立交．左图是该立交桥的部分道路示意图（道路宽度忽略不计），A为立交桥入口，D、G为出口，其中直行道为AB、CD、FG，且AB＝CD＝FG；弯道是以点O为圆心的一段弧，且BC、CE、EF所在的圆心角均为90°．甲、乙两车由A口同时驶入立交桥，均以16m/s的速度行驶，从不同出口驶出，其间两车到点O的距离y（m）与时间x（s）的对应关系如右图所示．结合题目信息，下列说法错误的是（ ）
A．该段立交桥总长为672m
B．从G口出比从D口出多行驶192m
C．甲车在立交桥上共行驶22s
D．甲车从G口出，乙车从D口出
【答案】D
【分析】根据题意，根据弧长公式并结合图象问题可得．
【详解】解：由图象可知，两车通过，，时每段所用时间均为6s，通过直行道AB，CG，EF时，每段用时为8s，
根据题意立交桥总长为（3×6+3×8）×16＝672m，故A不符合题意；
根据两车运行路线，从G口出比从D口出多走，弧长之和，用时为12s，则走12×16＝192m，故B不符合题意；
甲车在立交桥上共行驶时间为8+6+8＝22s，故C不符合题意；
根据两车运行时间，可知甲先驶出，应从D口驶出，乙车从G口出，故D符合题意．
故选：D．
【点睛】本题考查了动点问题的函数图象，解答时要注意数形结合．
40．（2023•滨城区一模）如图，点A，B是半径为2的⊙O上的两点，且，则下列说法正确的是（ ）
A．圆心O到AB的距离为
B．在圆上取异于A，B的一点C，则△ABC面积的最大值为
C．以AB为边向上作正方形，与⊙O的公共部分的面积为
D．取AB的中点C，当AB绕点O旋转一周时，点C运动的路线长为3π
【答案】B
【分析】连接AB、OA，过O作OG⊥AB于G，则得，由勾股定理求得OG的长，从而可判断A；由，其中h为AB上的高，则当h最大时，面积也最大，求出h的值即可求得最大面积，从而可判断B；由选项A的计算知，∠AOG＝∠MOF＝60°，直角所对的弦是直径，由三角形中位线定理得BF＝2OG＝2，分别求出梯形与扇形的面积，则梯形与扇形面积和的2倍即为所求的公共面积，从而可对选项C作出判断；易得点C的运动路径是圆，则可求得圆的周长，从而可判断D选项．
【详解】解：A、如图，连接AB、OA，过O作OG⊥AB于G，则，又圆的半径为2，由勾股定理得，即圆心O到AB的距离为1，故选项A错误；
B、如图，，其中h为AB上的高，则当h最大时，面积也最大，
此时C、O、G三点共线，且CG⊥AB，
而h＝CG＝OC+OG＝2+1＝3，则，
即△ABC面积的最大值为，故选项B正确；
C、如图，设GO的延长线交⊙O于点M，设AD、BC分别交⊙O于点E、F，连接OE、OF；
由选项A的计算知，，则∠AOG＝∠MOF＝60°，
由于四边形ABCD是正方形，∠ABC＝90°，则AF是直径，
所以由三角形中位线定理得BF＝2OG＝2，
而，，
则正方形与⊙O的公共部分的面积为，故选项C错误；
D、当AB绕点O旋转一周时，点C运动的路线是一个以O为圆心半径为1的圆，则圆周长为，所以点C运动的路线长为2π，故选项D错误．
故选：B．
【点睛】本题考查了直角对的弦是直径，垂径定理，勾股定理，正方形的性质，三角形中位线定理，锐角三角函数，求扇形的面积等知识，灵活运用这些知识是解题的关键．
声明：试题解析著作权属所有，未经书面同意，不得复制发布日期：2023/5/23 14:04:24；用户：数学1；邮箱：yz102@xyh.cm；学号：31595942