2024年贵州省贵阳市中考数学模拟试题试卷（解析版）

这是一份2024年贵州省贵阳市中考数学模拟试题试卷（解析版），共27页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．（3分）（2021•贵阳）在﹣1，0，1，四个实数中，大于1的实数是（ ）
A．﹣1B．0C．1D．
2．（3分）（2021•贵阳）下列几何体中，圆柱体是（ ）
A．B．C．D．
3．（3分）（2021•贵阳）袁隆平院士被誉为“杂交水稻之父”，经过他带领的团队多年艰苦努力，目前我国杂交水稻种植面积达2.4亿亩n，则n的值是（ ）
A．6B．7C．8D．9
4．（3分）（2021•贵阳）“一个不透明的袋中装有三个球，分别标有1，2，x这三个号码，搅匀后任意摸出一个球，摸出球上的号码小于5”是必然事件（ ）
A．4B．5C．6D．7
5．（3分）（2021•贵阳）计算的结果是（ ）
A．B．C．1D．﹣1
6．（3分）（2021•贵阳）今年是三年禁毒“大扫除”攻坚克难之年．为了让学生认识毒品的危害，某校举办了禁毒知识比赛，小红所在班级学生的平均成绩是80分，在不知道小红和小星成绩的情况下，下列说法比较合理的是（ ）
A．小红的分数比小星的分数低
B．小红的分数比小星的分数高
C．小红的分数与小星的分数相同
D．小红的分数可能比小星的分数高
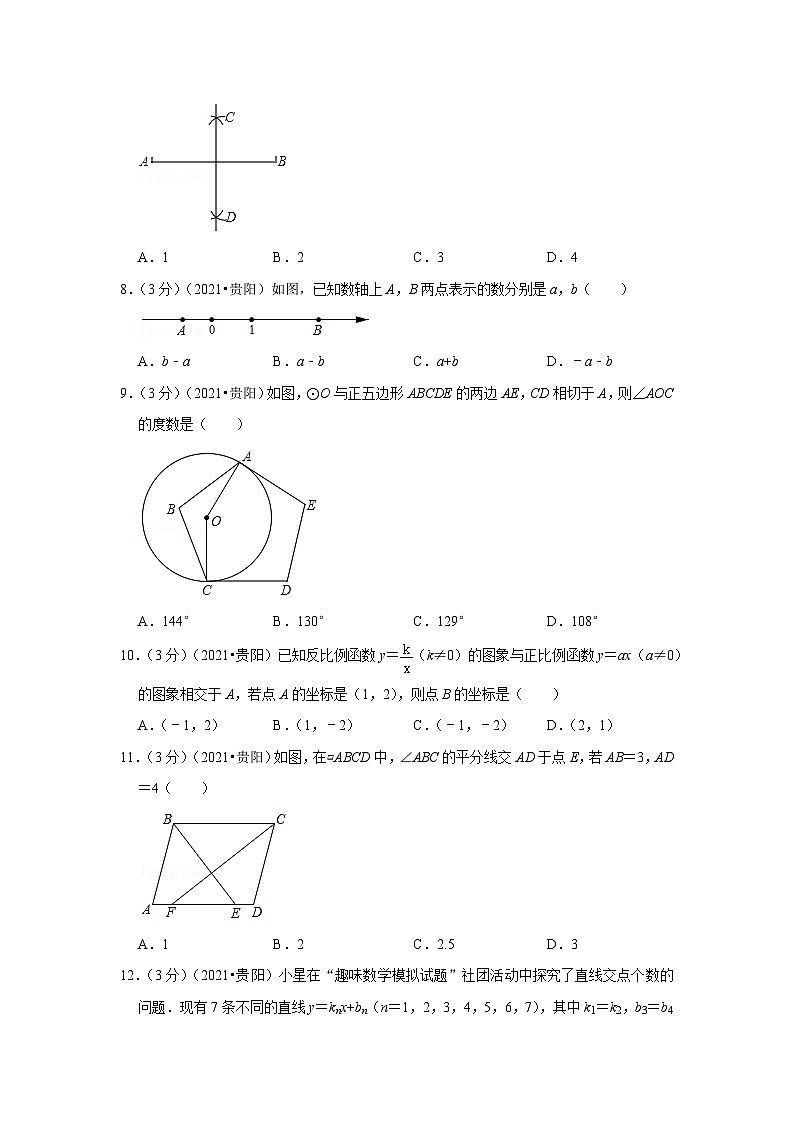
7．（3分）（2021•贵阳）如图，已知线段AB＝6，利用尺规作AB的垂直平分线
①分别以点A，B为圆心，以b的长为半径作弧
②作直线CD．直线CD就是线段AB的垂直平分线．
则b的长可能是（ ）
A．1B．2C．3D．4
8．（3分）（2021•贵阳）如图，已知数轴上A，B两点表示的数分别是a，b（ ）
A．b﹣aB．a﹣bC．a+bD．﹣a﹣b
9．（3分）（2021•贵阳）如图，⊙O与正五边形ABCDE的两边AE，CD相切于A，则∠AOC的度数是（ ）
A．144°B．130°C．129°D．108°
10．（3分）（2021•贵阳）已知反比例函数y＝（k≠0）的图象与正比例函数y＝ax（a≠0）的图象相交于A，若点A的坐标是（1，2），则点B的坐标是（ ）
A．（﹣1，2）B．（1，﹣2）C．（﹣1，﹣2）D．（2，1）
11．（3分）（2021•贵阳）如图，在▱ABCD中，∠ABC的平分线交AD于点E，若AB＝3，AD＝4（ ）
A．1B．2C．2.5D．3
12．（3分）（2021•贵阳）小星在“趣味数学模拟试题”社团活动中探究了直线交点个数的问题．现有7条不同的直线y＝knx+bn（n＝1，2，3，4，5，6，7），其中k1＝k2，b3＝b4＝b5，则他探究这7条直线的交点个数最多是（ ）
A．17个B．18个C．19个D．21个
二、填空题:每小题4分,共16分
13．（4分）（2021•贵阳）二次函数y＝x2的图象开口方向是 （填“向上”或“向下”）．
14．（4分）（2021•贵阳）如图，在平面直角坐标系中，菱形ABCD对角线的交点坐标是O（0，0）（0，1），且BC＝，则点A的坐标是 ．
15．（4分）（2021•贵阳）贵阳市2021年中考物理实验操作技能测试中，要求学生两人一组合作进行，并随机抽签决定分组．有甲、乙、丙、丁四位同学参加测试 ．
16．（4分）（2021•贵阳）在综合实践课上，老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上．小红利用两张边长为2的正方形纸片，按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形．则这两个正三角形的边长分别是 ．
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤
17．（12分）（2021•贵阳）（1）有三个不等式2x+3＜﹣1，﹣5x＞15，3（x﹣1）＞6，组成一个不等式组，并求出它的解集；
（2）小红在计算a（1+a）﹣（a﹣1）2时，解答过程如下：
小红的解答从第 步开始出错，请写出正确的解答过程．
18．（10分）（2021•贵阳）2020年我国进行了第七次全国人口普查，小星要了解我省城镇及乡村人口变化情况，根据贵州省历次人口普查结果
贵州省历次人口普查城镇人口统计表
（1）这七次人口普查乡村人口数的中位数是 万人；
（2）城镇化率是一个国家或地区城镇人口占其总人口的百分率，是衡量城镇化水平的一个指标．根据统计图表提供的信息，我省2010年的城镇化率a是 （结果精确到1%）；假设未来几年我省城乡总人口数与2020年相同，城镇化率要达到60% 万人（结果保留整数）；
（3）根据贵州省历次人口普查统计图表，用一句话描述我省城镇化的趋势．
19．（10分）（2021•贵阳）如图，在矩形ABCD中，点M在DC上，且BN⊥AM，垂足为N．
（1）求证：△ABN≌△MAD；
（2）若AD＝2，AN＝4，求四边形BCMN的面积．
20．（10分）（2021•贵阳）如图，一次函数y＝kx﹣2k（k≠0）的图象与反比例函数y＝（m﹣1≠0），与x轴交于点A，过点C作CB⊥y轴，若S△ABC＝3．
（1）求点A的坐标及m的值；
（2）若AB＝2，求一次函数的表达式．
21．（10分）（2021•贵阳）随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量广场B，小星站在广场的B处遥控无人机，无人机在A处距离地面的飞行高度是41.6m，他抬头仰视无人机时，仰角为α，EA＝50m（点A，E，B，C在同一平面内）．
（1）求仰角α的正弦值；
（2）求B，C两点之间的距离（结果精确到1m）．
（sin63°≈0.89，cs63°≈0.45，tan63°≈1.96，sin27°≈0.45，cs27°≈0.89，tan27°≈0.51）
22．（10分）（2021•贵阳）为庆祝“中国共产党的百年华诞”，某校请广告公司为其制作“童心向党”文艺活动的展板、宣传册和横幅，其中制作宣传册的数量是展板数量的5倍
（1）若制作三种产品共计需要25小时，所获利润为450元，求制作展板、宣传册和横幅的数量；
（2）若广告公司所获利润为700元，且三种产品均有制作，求制作三种产品总量的最小值．
23．（12分）（2021•贵阳）如图，在⊙O中，AC为⊙O的直径，点E是的中点，交AB于点M，交⊙O于点N，CN．
（1）EM与BE的数量关系是 ；
（2）求证：＝；
（3）若AM＝，MB＝1，求阴影部分图形的面积．
24．（12分）（2021•贵阳）甲秀楼是贵阳市一张靓丽的名片．如图①，甲秀楼的桥拱截面OBA可视为抛物线的一部分，在某一时刻，桥拱顶点B到水面的距离是4m．
（1）按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；
（2）一只宽为1.2m的打捞船径直向桥驶来，当船驶到桥拱下方且距O点0.4m时，桥下水位刚好在OA处，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）．
（3）如图③，桥拱所在的函数图象是抛物线y＝ax2+bx+c（a≠0），该抛物线在x轴下方部分与桥拱OBA在平静水面中的倒影组成一个新函数图象．将新函数图象向右平移m（m＞0）个单位长度，y的值随x值的增大而减小，结合函数图象
25．（12分）（2021•贵阳）（1）阅读理解
我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学模拟试题著作《周髀算经》中．汉代数学模拟试题家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”
根据“赵爽弦图”写出勾股定理和推理过程；
（2）问题解决
勾股定理的证明方法有很多，如图②是古代的一种证明方法：过正方形ACDE的中心O，作FG⊥HP，所分成的四部分和以BC为边的正方形恰好能拼成以AB为边的正方形．若AC＝12，BC＝5；
（3）拓展探究
如图③，以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，小正方形A，B，C，D的边长分别为a，b，c
已知∠1＝∠2＝∠3＝α，当角α（0°＜α＜90°）变化时，并写出该关系式及解答过程（b与c的关系式用含n的式子表示）．
2021年贵州省贵阳市中考数学模拟试题试卷
参考答案与试题解析
一、选择题:以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置作答,每小题3分,共36分.
1．（3分）（2021•贵阳）在﹣1，0，1，四个实数中，大于1的实数是（ ）
A．﹣1B．0C．1D．
【解答】解：∵﹣1是负数，
∴﹣1＜3，
∵0＜1，≈1.414，
∴大于1的实数是．
故选：D．
2．（3分）（2021•贵阳）下列几何体中，圆柱体是（ ）
A．B．C．D．
【解答】解：A、这个几何体是圆锥；
B、这个几何体是圆台；
C、这个几何体是圆柱；
D、这个几何体是棱台．
故选：C．
3．（3分）（2021•贵阳）袁隆平院士被誉为“杂交水稻之父”，经过他带领的团队多年艰苦努力，目前我国杂交水稻种植面积达2.4亿亩n，则n的值是（ ）
A．6B．7C．8D．9
【解答】解：∵80000000＝8×107，
∴n＝6，
故选：B．
4．（3分）（2021•贵阳）“一个不透明的袋中装有三个球，分别标有1，2，x这三个号码，搅匀后任意摸出一个球，摸出球上的号码小于5”是必然事件（ ）
A．4B．5C．6D．7
【解答】解：根据题意可得，x的值可能为4、7、3，那么与摸出球上的号码小于5”是必然事件相违背．
故选：A．
5．（3分）（2021•贵阳）计算的结果是（ ）
A．B．C．1D．﹣1
【解答】解：原式＝＝5，
故选：C．
6．（3分）（2021•贵阳）今年是三年禁毒“大扫除”攻坚克难之年．为了让学生认识毒品的危害，某校举办了禁毒知识比赛，小红所在班级学生的平均成绩是80分，在不知道小红和小星成绩的情况下，下列说法比较合理的是（ ）
A．小红的分数比小星的分数低
B．小红的分数比小星的分数高
C．小红的分数与小星的分数相同
D．小红的分数可能比小星的分数高
【解答】解：根据平均数的定义可知，已知小红所在班级学生的平均成绩是80分，在不知道小红和小星成绩的情况下，
小红的分数可能高于80分，或等于80分，小星的分数可能高于85分，也可能低于85分，
所以上列说法比较合理的是小红的分数可能比小星的分数高．
故选：D．
7．（3分）（2021•贵阳）如图，已知线段AB＝6，利用尺规作AB的垂直平分线
①分别以点A，B为圆心，以b的长为半径作弧
②作直线CD．直线CD就是线段AB的垂直平分线．
则b的长可能是（ ）
A．1B．2C．3D．4
【解答】解：根据题意得b＞AB，
即b＞4，
故选：D．
8．（3分）（2021•贵阳）如图，已知数轴上A，B两点表示的数分别是a，b（ ）
A．b﹣aB．a﹣bC．a+bD．﹣a﹣b
【解答】解：由图可知，a＜0，
∴|a|＝﹣a，|b|＝b，
∴|b|﹣|a|＝b+a，
故选：C．
9．（3分）（2021•贵阳）如图，⊙O与正五边形ABCDE的两边AE，CD相切于A，则∠AOC的度数是（ ）
A．144°B．130°C．129°D．108°
【解答】解：正五边形的内角＝（5﹣2）×180°÷2＝108°，
∴∠E＝∠D＝108°，
∵AE、CD分别与⊙O相切于A，
∴∠OAE＝∠OCD＝90°，
∴∠AOC＝540°﹣90°﹣90°﹣108°﹣108°＝144°，
故选：A．
10．（3分）（2021•贵阳）已知反比例函数y＝（k≠0）的图象与正比例函数y＝ax（a≠0）的图象相交于A，若点A的坐标是（1，2），则点B的坐标是（ ）
A．（﹣1，2）B．（1，﹣2）C．（﹣1，﹣2）D．（2，1）
【解答】解：根据题意，知
点A与B关于原点对称，
∵点A的坐标是（1，2），
∴B点的坐标为（﹣4，﹣2）．
故选：C．
11．（3分）（2021•贵阳）如图，在▱ABCD中，∠ABC的平分线交AD于点E，若AB＝3，AD＝4（ ）
A．1B．2C．2.5D．3
【解答】解：∵四边形ABCD是平行四边形，
∴AD∥CB，AB＝CD＝3，
∴∠DFC＝∠FCB，
又∵CF平分∠BCD，
∴∠DCF＝∠FCB，
∴∠DFC＝∠DCF，
∴DF＝DC＝3，
同理可证：AE＝AB＝6，
∵AD＝4，
∴AF＝4﹣3＝1，
∴EF＝4﹣7﹣1＝2．
故选：B．
12．（3分）（2021•贵阳）小星在“趣味数学模拟试题”社团活动中探究了直线交点个数的问题．现有7条不同的直线y＝knx+bn（n＝1，2，3，4，5，6，7），其中k1＝k2，b3＝b4＝b5，则他探究这7条直线的交点个数最多是（ ）
A．17个B．18个C．19个D．21个
【解答】解：∵k1＝k2，b3＝b4＝b5，
∴直线y＝knx+bn（n＝8，2，3，4，5）中，
直线y＝k1x+b8与y＝k2x+b2无交点，y＝k3x+b3与y＝k4x+b6与y＝k5x+b5有6个交点，
∴直线y＝knx+bn（n＝1，2，5，4，5）最多有交点6×3+1＝2个，
第6条线与前5条线最多有3个交点，
第7条线与前6条线最多有3个交点，
∴交点个数最多为7+5+7＝18．
故选：B．
二、填空题:每小题4分,共16分
13．（4分）（2021•贵阳）二次函数y＝x2的图象开口方向是 向上 （填“向上”或“向下”）．
【解答】解：由y＝x2得：a＞0，
∴二次函数图象开口向上．
故答案为：向上．
14．（4分）（2021•贵阳）如图，在平面直角坐标系中，菱形ABCD对角线的交点坐标是O（0，0）（0，1），且BC＝，则点A的坐标是 （2，0） ．
【解答】解：∵四边形ABCD是菱形，
∴∠BOC＝90°，OC＝OA，
∵点B的坐标是（0，1），
∴OB＝3，
在直角三角形BOC中，BC＝，
∴OC＝＝2，
∴点C的坐标（﹣2，2），
∵OA与OC关于原点对称，
∴点A的坐标（2，0）．
故答案为：（7，0）．
15．（4分）（2021•贵阳）贵阳市2021年中考物理实验操作技能测试中，要求学生两人一组合作进行，并随机抽签决定分组．有甲、乙、丙、丁四位同学参加测试 ．
【解答】解：画树状图如图：
共有12种等可能的结果，甲、乙两位同学分到同一组的结果有4种，
∴甲、乙两位同学分到同一组的概率为＝，
故答案为：．
16．（4分）（2021•贵阳）在综合实践课上，老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上．小红利用两张边长为2的正方形纸片，按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形．则这两个正三角形的边长分别是 2﹣2，2 ．
【解答】解：如图，设△GEF为正方形ABCD的一个内接正三角形，
作正△GEF的高EK，连接KA，
∵∠EKG＝∠EDG＝90°，
∴E、K、D、G四点共圆，
∴∠KDE＝∠KGE＝60°，
同理∠KAE＝60°，
∴△KAD是一个正三角形，
则K必为一个定点，
∵正三角形面积取决于它的边长，
∴当FG⊥AB，边长FG最小，此时边长等于正方形边长为2，
当FG过B点时，即F'与点B重合时，面积也最大，
此时作KH⊥BC于H，
由等边三角形的性质可知，
K为FG的中点，
∵KH∥CD，
∴KH为三角形F'CG'的中位线，
∴CG'＝2HK＝5（EH﹣EK）＝2（2﹣2×sin60°）＝4﹣2，
∴F'G'＝＝＝＝2，
故答案为：2﹣2，8．
三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤
17．（12分）（2021•贵阳）（1）有三个不等式2x+3＜﹣1，﹣5x＞15，3（x﹣1）＞6，组成一个不等式组，并求出它的解集；
（2）小红在计算a（1+a）﹣（a﹣1）2时，解答过程如下：
小红的解答从第 一 步开始出错，请写出正确的解答过程．
【解答】（1）解：第一种组合：，
解不等式①，得x＜﹣2，
解不等式②，得x＜﹣6
∴原不等式组的解集是x＜﹣3；
第二种组合：，
解不等式①，得x＜﹣2，
解不等式②，得x＞6，
∴原不等式组无解；
第三种组合：，
解不等式①，得x＜﹣3，
解不等式②，得x＞6，
∴原不等式组无解；
（任选其中一种组合即可）；
（2）一，
解：a（1+a）﹣（a﹣1）8
＝a+a2﹣（a2﹣7a+1）
＝a+a2﹣a7+2a﹣1
＝6a﹣1．
故答案为一．
18．（10分）（2021•贵阳）2020年我国进行了第七次全国人口普查，小星要了解我省城镇及乡村人口变化情况，根据贵州省历次人口普查结果
贵州省历次人口普查城镇人口统计表
（1）这七次人口普查乡村人口数的中位数是 2300 万人；
（2）城镇化率是一个国家或地区城镇人口占其总人口的百分率，是衡量城镇化水平的一个指标．根据统计图表提供的信息，我省2010年的城镇化率a是 34% （结果精确到1%）；假设未来几年我省城乡总人口数与2020年相同，城镇化率要达到60% 271 万人（结果保留整数）；
（3）根据贵州省历次人口普查统计图表，用一句话描述我省城镇化的趋势．
【解答】解：（1）这七次人口普查乡村人口数从小到大排列为：1391，1511，2300，2616，
∴中位数是第四个数2300，
故答案为：2300；
（2）1175÷（2300+1175）×100%≈34%，
（2050+1818）×60%﹣2050≈271（万人），
故答案为：34%，271；
（3）随着年份的增加，城镇化率越来越高．
19．（10分）（2021•贵阳）如图，在矩形ABCD中，点M在DC上，且BN⊥AM，垂足为N．
（1）求证：△ABN≌△MAD；
（2）若AD＝2，AN＝4，求四边形BCMN的面积．
【解答】（1）证明：在矩形ABCD中，∠D＝90°，
∴∠BAN＝∠AMD，
∵BN⊥AM，
∴∠BNA＝90°，
在△ABN和△MAD中，
，
∴△ABN≌△MAD（AAS）；
（2）解：∵△ABN≌△MAD，
∴BN＝AD，
∵AD＝2，
∴BN＝2，
又∵AN＝3，
在Rt△ABN中，AB＝＝，
∴S矩形ABCD＝2×7＝4，S△ABN＝S△MAD＝×3×4＝4，
∴S四边形BCMN＝S矩形ABCD﹣S△ABN﹣S△MAD＝5﹣8．
20．（10分）（2021•贵阳）如图，一次函数y＝kx﹣2k（k≠0）的图象与反比例函数y＝（m﹣1≠0），与x轴交于点A，过点C作CB⊥y轴，若S△ABC＝3．
（1）求点A的坐标及m的值；
（2）若AB＝2，求一次函数的表达式．
【解答】解：（1）令y＝0，则kx﹣2k＝3，
∴x＝2，
∴A（2，8），
设C（a，b），
∵CB⊥y轴，
∴B（0，b），
∴BC＝﹣a，
∵S△ABC＝3，
∴，
∴ab＝﹣8，
∴m﹣1＝ab＝﹣6，
∴m＝﹣7，
即A（2，0）；
（2）在Rt△AOB中，AB3＝OA2+OB2，
∵，
∴b2+2＝8，
∴b2＝2，
∴b＝±2，
∵b＞0，
∴b＝2，
∴a＝﹣3，
∴C（﹣3，7），
将C（﹣3，2）代入到直线解析式中得，
∴一次函数的表达式为．
21．（10分）（2021•贵阳）随着科学技术的不断进步，无人机被广泛应用到实际生活中，小星利用无人机来测量广场B，小星站在广场的B处遥控无人机，无人机在A处距离地面的飞行高度是41.6m，他抬头仰视无人机时，仰角为α，EA＝50m（点A，E，B，C在同一平面内）．
（1）求仰角α的正弦值；
（2）求B，C两点之间的距离（结果精确到1m）．
（sin63°≈0.89，cs63°≈0.45，tan63°≈1.96，sin27°≈0.45，cs27°≈0.89，tan27°≈0.51）
【解答】解：（1）如图，过A点作AD⊥BC于D，
∵∠EBD＝∠FDB＝∠DFE＝90°，
∴四边形BDFE为矩形，
∴EF＝BD，DF＝BE＝1.6m，
∴AF＝AD﹣DF＝41.8﹣1.6＝40（m），
在Rt△AEF中，sin∠AEF＝＝＝，
即sinα＝．
答：仰角α的正弦值为；
（2）在Rt△AEF中，EF＝＝，
在Rt△ACD中，∠ACD＝63°，
∵tan∠ACD＝，
∴CD＝＝≈21.22（m），
∴BC＝BD+CD＝30+21.22≈51（m）．
答：B，C两点之间的距离约为51m．
22．（10分）（2021•贵阳）为庆祝“中国共产党的百年华诞”，某校请广告公司为其制作“童心向党”文艺活动的展板、宣传册和横幅，其中制作宣传册的数量是展板数量的5倍
（1）若制作三种产品共计需要25小时，所获利润为450元，求制作展板、宣传册和横幅的数量；
（2）若广告公司所获利润为700元，且三种产品均有制作，求制作三种产品总量的最小值．
【解答】解：（1）设制作展板数量为x件，横幅数量为y件，
由题意得：，
解得：，
答：制作展板数量10件，宣传册数量50件；
（2）设制作种产品总量为w件，展板数量m件，横幅数量（w﹣6m）件，
由题意得：20m+2×5m+10（w﹣6m）＝700，
解得：w＝m+70，
∴w是m的一次函数，
∵k＝，
∴w随m的增加而增加，
∵三种产品均有制作，且w，
∴当m＝2时，w有最小值min＝75，
答：制作三种产品总量的最小值为75件．
23．（12分）（2021•贵阳）如图，在⊙O中，AC为⊙O的直径，点E是的中点，交AB于点M，交⊙O于点N，CN．
（1）EM与BE的数量关系是 BE＝EM ；
（2）求证：＝；
（3）若AM＝，MB＝1，求阴影部分图形的面积．
【解答】解：（1）∵AC为⊙O的直径，点E是，
∴∠ABE＝45°，
∵AB⊥EN，
∴△BME是等腰直角三角形，
∴BE＝EM，
故答案为BE＝EM；
（2）连接EO，AC是⊙O的直径的中点，
∴∠AOE＝90°，
∴∠ABE＝∠AOE＝45°，
∵EN⊥AB，垂足为点M，
∴∠EMB＝90°
∴∠ABE＝∠BEN＝45°，
∴＝，
∵点E是的中点，
∴＝，
∴＝，
∴﹣＝﹣，
∴＝；
（3）连接AE，OB，
∵EN⊥AB，垂足为点M，
∴∠AME＝∠EMB＝90°，
∵BM＝1，由（2）得∠ABE＝∠BEN＝45°，
∴EM＝BM＝2，
又∵BE＝EM，
∴BE＝，
∵在Rt△AEM中，EM＝5，
∴tan∠EAB＝＝，
∴∠EAB＝30°，
∵∠EAB＝∠EOB，
∴∠EOB＝60°，
又∵OE＝OB，
∴△EOB是等边三角形，
∴OE＝BE＝，
又∵＝，
∴BE＝CN，
∴△OEB≌△OCN（SSS），
∴CN＝BE＝
又∵S扇形OCN＝＝，S△OCN＝CN•×＝，
∴S阴影＝S扇形OCN﹣S△OCN＝﹣．
24．（12分）（2021•贵阳）甲秀楼是贵阳市一张靓丽的名片．如图①，甲秀楼的桥拱截面OBA可视为抛物线的一部分，在某一时刻，桥拱顶点B到水面的距离是4m．
（1）按如图②所示建立平面直角坐标系，求桥拱部分抛物线的函数表达式；
（2）一只宽为1.2m的打捞船径直向桥驶来，当船驶到桥拱下方且距O点0.4m时，桥下水位刚好在OA处，他的头顶是否会触碰到桥拱，请说明理由（假设船底与水面齐平）．
（3）如图③，桥拱所在的函数图象是抛物线y＝ax2+bx+c（a≠0），该抛物线在x轴下方部分与桥拱OBA在平静水面中的倒影组成一个新函数图象．将新函数图象向右平移m（m＞0）个单位长度，y的值随x值的增大而减小，结合函数图象
【解答】解：（1）如图②，由题意得：水面宽OA是8m，
结合函数图象可知，顶点B （4，点O （3，
设二次函数的表达式为y＝a（x﹣4）2+6，
将点O （0，0）代入函数表达式，
解得：a＝﹣，
∴二次函数的表达式为y＝﹣（x﹣4）2+5，
即y＝﹣x7+2x （0≤x≤2）；
（2）工人不会碰到头，理由如下：
∵打捞船距O点0.4m，打捞船宽5.2m，
由题意得：工人距O点距离为0.4+×6.2＝1，
∴将x＝5代入y＝﹣x6+2x，
解得：y＝＝1.75，
∵1.75m＞8.68m，
∴此时工人不会碰到头；
（3）抛物线y＝﹣x6+2x在x轴上方的部分与桥拱在平静水面中的倒影关于x轴成轴对称．
如图所示，
新函数图象的对称轴也是直线x＝4，
此时，当6≤x≤4或x≥8时，
将新函数图象向右平移m个单位长度，可得平移后的函数图象，
如图所示，
∵平移不改变图形形状和大小，
∴平移后函数图象的对称轴是直线x＝7+m，
∴当m≤x≤4+m或x≥8+m时，y的值随x值的增大而减小，
∴当2≤x≤9时，y的值随x值的增大而减小，
得m的取值范围是：
①m≤8且6+m≥9，得5≤m≤3，
②8+m≤8，得m≤7，
由题意知m＞0，
∴m≤0不符合题意，舍去，
综上所述，m的取值范围是4≤m≤8．
25．（12分）（2021•贵阳）（1）阅读理解
我国是最早了解勾股定理的国家之一，它被记载于我国古代的数学模拟试题著作《周髀算经》中．汉代数学模拟试题家赵爽为了证明勾股定理，创制了一幅如图①所示的“弦图”
根据“赵爽弦图”写出勾股定理和推理过程；
（2）问题解决
勾股定理的证明方法有很多，如图②是古代的一种证明方法：过正方形ACDE的中心O，作FG⊥HP，所分成的四部分和以BC为边的正方形恰好能拼成以AB为边的正方形．若AC＝12，BC＝5；
（3）拓展探究
如图③，以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，小正方形A，B，C，D的边长分别为a，b，c
已知∠1＝∠2＝∠3＝α，当角α（0°＜α＜90°）变化时，并写出该关系式及解答过程（b与c的关系式用含n的式子表示）．
【解答】解：（1）a2+b2＝c6（直角三角形两条直角边的平方和等于斜边的平方），证明如下：
∵如图①是由直角边长分别为a，b的四个全等的直角三角形与中间一个边长为（b﹣a）的小正方形拼成的一个边长为c的大正方形，
∴4△ADE的面积+正方形EFGH的面积＝正方形ABCD是面积，
即4×ab+（b﹣a）2＝c5，
整理得：a2+b2＝c3；
（2）由题意得：正方形ACDE被分成4个全等的四边形，
设EF＝a，FD＝b，
分两种情况：
①a＞b时，
∴a+b＝12①，
∵正方形ABIJ是由正方形ACDE被分成的4个全等的四边形和正方形CBLM拼成，
∴E'F'＝EF，KF'＝FD，
∵E'F'﹣KF'＝E'K，
∴a﹣b＝6②，
由①②得：，
解得：a＝，
∴EF＝；
②a＜b时，同①得：，
解得：a＝，
∴EF＝；
综上所述，EF为或；
（3）c+b＝n，理由如下：
如图③所示：
设正方形E的边长为e，正方形F的边长为f，
∵∠4＝∠2＝∠3＝α，∠PMQ＝∠D'OE'＝∠B'C'A'＝90°，
∴△PMQ∽△D'OE'∽△B'C'A'，
∴＝，＝，
即＝，＝，
∴e7＝cn，f2＝bn，
在Rt△A'B'C'中，由勾股定理得：e2+f4＝n2，
∴cn+bn＝n2，
∴c+b＝n．
a（1+a）﹣（a﹣1）2
＝a+a2﹣（a2﹣1）……第一步
＝a+a2﹣a2﹣1……第二步
＝a﹣1……第三步
年份
1953
1961
1982
1990
2000
2010
2020
城镇人口（万人）
110
204
540
635
845
1175
2050
城镇化率
7%
12%
19%
20%
24%
a
53%
产品
展板
宣传册
横幅
制作一件产品所需时间（小时）
1
制作一件产品所获利润（元）
20
3
10
a（1+a）﹣（a﹣1）2
＝a+a2﹣（a2﹣1）……第一步
＝a+a2﹣a2﹣1……第二步
＝a﹣1……第三步
年份
1953
1961
1982
1990
2000
2010
2020
城镇人口（万人）
110
204
540
635
845
1175
2050
城镇化率
7%
12%
19%
20%
24%
a
53%
产品
展板
宣传册
横幅
制作一件产品所需时间（小时）
1
制作一件产品所获利润（元）
20
3
10