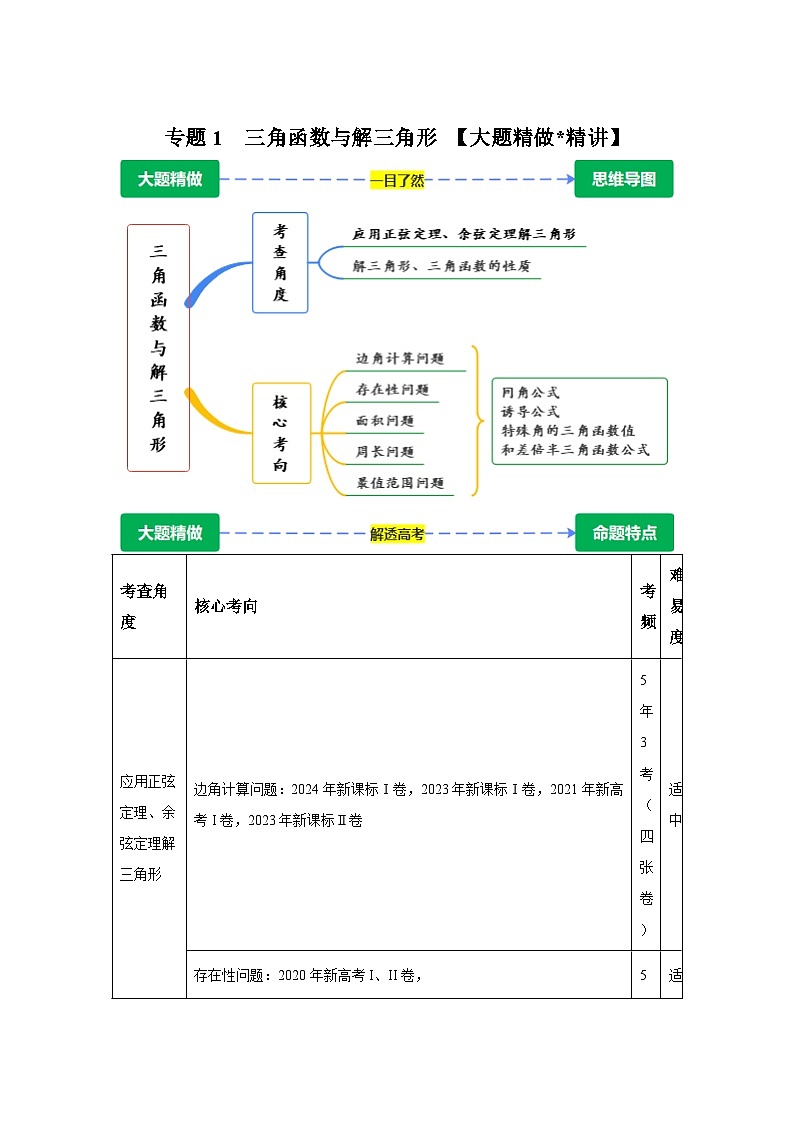
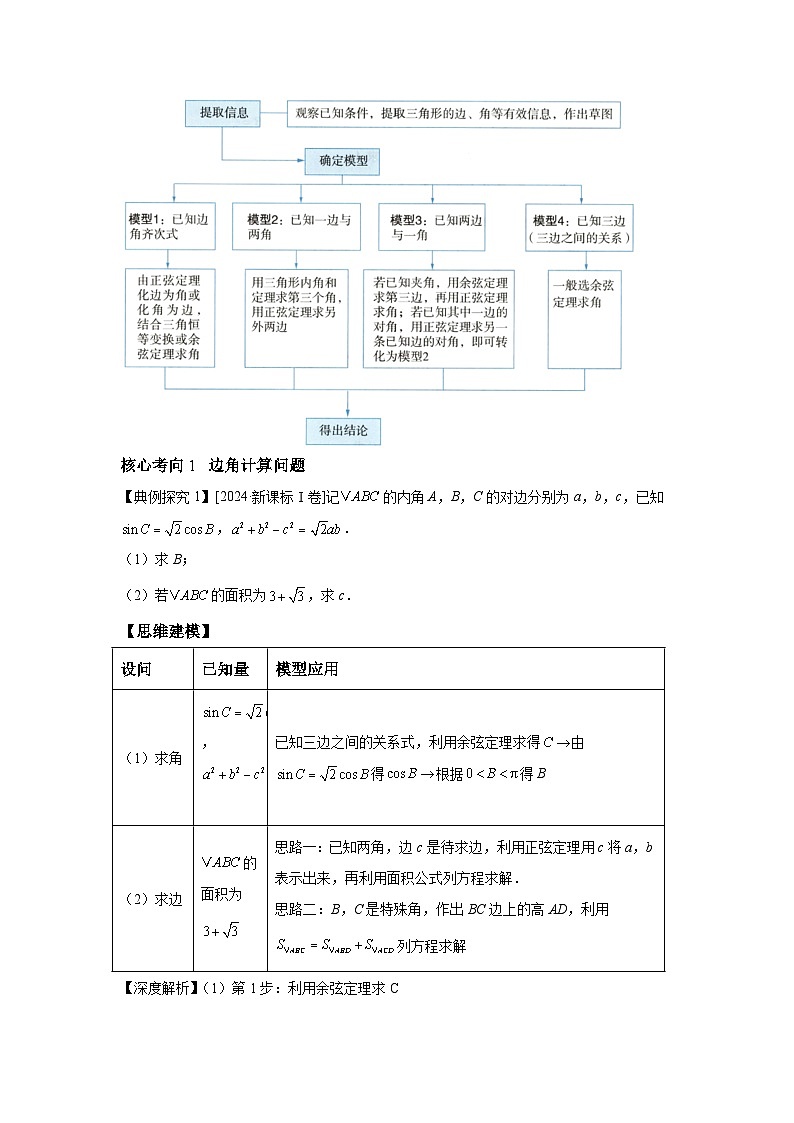
专题1三角函数与解三角形【讲】-2025年高考数学大题精做讲练（题型破局）附答案解析

这是一份专题1三角函数与解三角形【讲】-2025年高考数学大题精做讲练（题型破局）附答案解析，共20页。

【模版构建】
核心考向1 边角计算问题
【典例探究1】[2024·新课标Ⅰ卷]记的内角A，B，C的对边分别为a，b，c，已知，．
（1）求B；
（2）若的面积为，求c．
【思维建模】
【深度解析】（1）第1步：利用余弦定理求C
因为，所以由余弦定理有，（2分）
因为，所以．（3分）
第2步：代入已知等式求B
因为，所以．因为，所以．（6分）
（2）方法一第1步：利用三角形内角和定理求A
由（1）知，，所以．（8分）
第2步：利用正弦定理用c表示a，b
，
【速解技巧】掌握并识记一些常见的三角函数值，如，等，可以提升解题速度
由正弦定理有，从而，．（10分）
第3步：利用三角形面积公式，求c
所以，解得．（13分）
方法二第1步：根据已知角作出图形，作BC边上的高AD，用c表示BD，AD，CD
由（1）知，．如图，作出，过A作BC边上的垂线，垂足为D，则，．（10分）
第2步：利用三角形面积公式“底×高”求c
因为的面积为，所以，解得．（13分）
【高分技法】必备知识 正、余弦定理及其变形的应用技法
在中，内角A，B，C所对的边分别是a，b，c，R为的外接圆半径．
必记结论 解三角形中的常用二级结论[链接变式2（2）]
【典例探究2】已知的内角A，B，C所对的边分别为a，b，c，．
（1）求B．
（2）若点D在线段AC上，且，求．
【思维建模】
【深度解析】
（1）因为，所以，
由正弦定理可得，整理得（【会观察】这是余弦定理的结构特征），（2分）
由余弦定理可得，（4分）
因为，所以．（5分）
（2）如图，因为，所以，
可得（【会思考】BD，BA，BC是同一顶点出发的三条线段．如何建立联系？考虑向量的工具作用，不如利用向量法．用一组基底表示），（7分）
则，即，（9分）
整理得，（10分）
由余弦定理可得，则（【解题技巧】通过对某一条边或某一个角在不同图形中“算两次”我等量关系是解三角形问题中常用的方法，两次余弦法也是“算两次”的体现之一），（12分）
即，所以．（13分）
核心考向2 存在性问题
【典例探究3】（2021年全国新高考II卷数学试题）在中，角、、所对的边长分别为、、，，.
（1）若，求的面积；
（2）是否存在正整数，使得为钝角三角形?若存在，求出的值；若不存在，说明理由．
【思维建模】
【深度解析】
（1）因为，则，则，故，，
，所以，为锐角，则，
因此，；
（2）显然，若为钝角三角形，则为钝角，
由余弦定理可得，
解得，则，
由三角形三边关系可得，可得，，故.
【典例探究4】（2025·湖南娄底·一模）已知的内角的对边分别为的内切圆圆的面积为.
(1)求的值及；
(2)若点在上，且三点共线，试讨论在边上是否存在点，使得若存在，求出点的位置，并求出的面积；若不存在，请说明理由.
【思维建模】
【深度解析】
（1）因为内切圆圆的面积为，可得圆的半径为，
则，
所以，由余弦定理得，
得，将代入整理得：，
解得.
由余弦定理得：.
（2）记圆与边切于点，根据切线长定理可求得，
若，则，
即，解得，
所以在边上存在点，使得.
依题意可知为内心，则平分，
记，则，
故，
在中，，
由正弦定理得，
又，
，.
核心考向3 最值范围问题
【典例探究5】（2022年新高考全国I卷）记的内角A，B，C的对边分别为a，b，c，已知．
(1)若，求B；
(2)求的最小值．
【思维建模】
【深度解析】
（1）因为，即，
而，所以；
（2）由（1）知，，所以，
而，
所以，即有，所以
所以
．
当且仅当时取等号，所以的最小值为．
【典例探究6】在中，D为BC边的中点，．
（1）若的面积为，且，求的值．
（2）若，求的周长的最大值．
【思维建模】
【深度解析】（1）如图（【会观察】解三角形问题一般不在题干上给出已知图形，需要我们自己动手画图、标注数据，从图中发现等量关系．如本题．根据图形得到大三角形的面积可转化为两个小三角形的面积和）
即，解得．（2分）
在中，，由余弦定理得，
即，解得．（4分）
再由正弦定理得，即，解得．（6分）
（2）设，则在中，，（7分）
在中，（8分）
又，可得，所以．（10分）
由基本不等式得，所以，当且仅当时去等号，（12分）
【易错提醒】注意基本不等式的变形使用及等号成立的条件，特别是在三角形中，注意验证三条边能否构成三角形
此时，所以的周长的最大值为．（13分）
核心考向4 周长问题
【典例探究7】（2024年新课标全国Ⅱ卷）记的内角A，B，C的对边分别为a，b，c，已知．
(1)求A．
(2)若，，求的周长．
【思维建模】
【深度解析】
（1）方法一：常规方法（辅助角公式）
由可得，即，
由于，故，解得
方法二：常规方法（同角三角函数的基本关系）
由，又，消去得到：
，解得，
又，故
方法三：利用极值点求解
设，则，
显然时，，注意到，
，在开区间上取到最大值，于是必定是极值点，
即，即，
又，故
方法四：利用向量数量积公式（柯西不等式）
设，由题意，，
根据向量的数量积公式，，
则，此时，即同向共线，
根据向量共线条件，，
又，故
方法五：利用万能公式求解
设，根据万能公式，，
整理可得，，
解得，根据二倍角公式，，
又，故
（2）由题设条件和正弦定理
，
又，则，进而，得到，
于是，
，
由正弦定理可得，，即，
解得，
故的周长为
【典例探究8】（24-25高三上·山东青岛·期中）的内角，，的对边分别为，，，已知.
(1)求角；
(2)若的面积为，为中点，，求的周长.
【思维建模】
【深度解析】
（1）由正弦定理得，
在中，，所以，
所以，
整理得，因为，所以，
因为，所以.
（2）在中，，所以①，
在中，，，，
由余弦定理得，
所以，所以②，
由①②得，，，在中，由余弦定理得，
所以，所以，的周长为.
（核心考向：边角计算问题）（24-25高三上·江苏南通·期中）
1．已知的内角、、的对边分别为、、，且．
(1)求；
(2)若，则面积为，求、的值．
（核心考向：面积问题）（24-25高三上·山东济宁·期末）
2．在中，角，，的对边分别为，，，已知.
(1)求证：；
(2)若，，求的面积.
（核心考向：存在性问题）（24-25高三上·山东滨州·期末）
3．中，内角，，所对的边分别为，，，已知．
(1)证明：；
(2)延长至点，使得，试探究是否为定值？并说明理由．
（核心考向：周长问题）（24-25高三上·山东青岛·阶段练习）
4．已知的内角的对边分别为.
(1)求的值；
(2)若的面积为，且，求的周长.
（核心考向：最值范围问题）（24-25高三上·河北石家庄·期中）
5．在中，角所对的边为且满足.
(1)求；
(2)当时，求边上中线的范围.
考查角度
核心考向
考频
难易度
应用正弦定理、余弦定理解三角形
边角计算问题：2024年新课标Ⅰ卷，2023年新课标Ⅰ卷，2021年新高考I卷，2023年新课标Ⅱ卷
5年3考
（四张卷）
适中
存在性问题：2020年新高考I、II卷，
2021年新高考II卷
5年2考
（三张卷）
适中
面积问题：2024年新课标Ⅰ卷，2022年新高考II卷，2021年全国新高考II卷
5年3考
适中
周长问题：2024年新课标Ⅱ卷，2020全国Ⅱ卷
5年2考
适中
最值范围问题：2022年新高考I卷，2020全国Ⅱ卷
5年2考
适中
解三角形、三角函数的性质
综合性：2020全国Ⅱ卷，考查周长最值问题，2022年新高考全国I卷，考查边长代数式的最小值，既可以利用三角函数的有界性、“对号函数”性质，也可以利用基本不等式求解，体现了命题的综合性和方法选取的灵活性
5年2考
适中
设问
已知量
模型应用
（1）求角
，
已知三边之间的关系式，利用余弦定理求得由得根据得B
（2）求边
的面积为
思路一：已知两角，边c是待求边，利用正弦定理用c将a，b表示出来，再利用面积公式列方程求解．
思路二：B，C是特殊角，作出BC边上的高AD，利用列方程求解
定理
正弦定理（已知两角一边或两边及其中一边对角）
余弦定理（已知三边或两边及其夹角）
内容
变式：
，
，
常见变形
（1）边化角：，，
（2）角化边：，，
（3）
求角或角化边：
，
，
定理整合
正、余弦整合定理：在中，．主要用于求值，如
三角形的面积公式
，其中R，r分别为外接圆、内切圆半径，p为周长的一半
1
射影定理
在中，，，
2
角平分线定理
在中，若AD是的平分线，点D在BC上，则有
3
中线定理
在中，AD是BC边上的中线，则
4
三角恒等式
在斜中，
5
两次余弦法
在中，点D在边BC上，则有，所以，即
设问
已知量
模型应用
（1）求角
由正弦定理角化边→结合余弦定理求角B
（2）求边的比值
利用图形中的向量关系以及余弦定理得关于a，c的等量关系，化简得
设问
已知量
模型应用
（1）求面积
，，
已知三边之间的关系式，正弦定理解方程组，求a，b，c;余弦定理求cssin C，根据面积公式得解
（2）探索边a存在性，为钝角三角形
为钝角三角形
由，若为钝角三角形，为钝角；应用余弦定理，csC