2024-2025学年天津市河东区高三上册第一次月考数学学情检测试卷（含解析）

这是一份2024-2025学年天津市河东区高三上册第一次月考数学学情检测试卷（含解析），共25页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题
1. 已知集合，则（ ）
A. B.
C. D.
2. 设，则“”是“”的
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
3. 函数在的图象大致为（ ）
A. B.
C. D.
4. 已知奇函数，且在上是增函数.若，，，则a，b，c的大小关系为
A. B.
C. D.
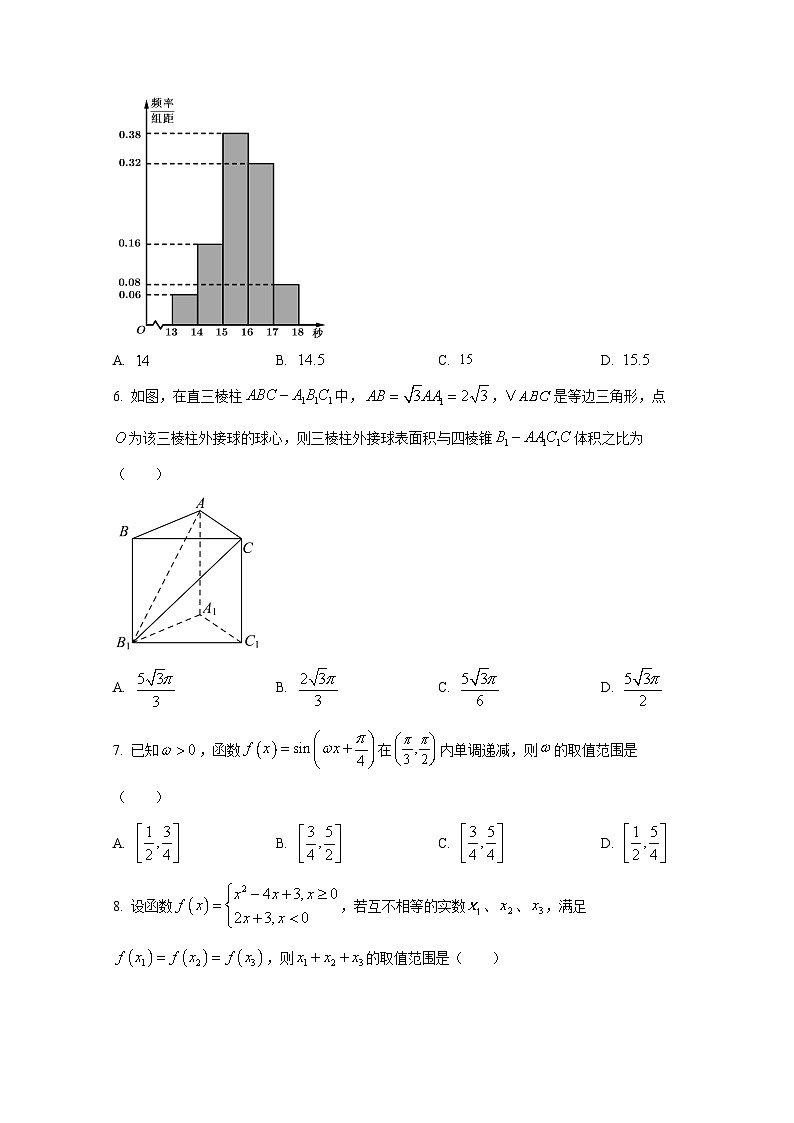
5. 某校抽取名学生做体能测认，其中百米测试中，成绩全部介于秒与秒之间，将测试结果分成五组：第一组，第二组，，第五组．如图是按上述分组方法得到频率分布直方图，若成绩低于即为优秀，如果优秀的人数为人，则的估计值是（ ）
A. B. C. D.
6. 如图，在直三棱柱中，，是等边三角形，点为该三棱柱外接球的球心，则三棱柱外接球表面积与四棱锥体积之比为（ ）
A. B. C. D.
7. 已知，函数在内单调递减，则的取值范围是（ ）
A. B. C. D.
8. 设函数，若互不相等的实数、、，满足，则的取值范围是（ ）
A. B. C. D.
9 已知，给出下列结论：
①若，且，则；
②存在，使得的图像向左平移个单位长度后得到的图像关于轴对称；
③若，则上单调递增；
④若在上恰有5个零点，则取值范围为.
其中，所有正确结论的个数是（ ）
A. 1B. 2C. 3D. 4
二、填空题
10. 是虚数单位，复数的虚部是______.
11. 在的展开式中，x的系数为_______．
12. 计算：______．
13. 设，，若，则的最小值为_____________.
14. 甲､乙两名枪手进行射击比赛，每人各射击三次，甲三次射击命中率均为；乙第一次射击的命中率为，若第一次未射中，则乙进行第二次射击，射击的命中率为，如果又未中，则乙进行第三次射击，射击的命中率为.乙若射中，则不再继续射击.则甲三次射击恰好命中1次的概率为______，乙射击次数的期望为______.
15. 在菱形ABCD中，，，E，F分别为线段BC，CD上的点，，，点M在线段EF上，且满足，则x=___________；若点N为线段BD上一动点，则的取值范围为___________.
三、解答题
16. 在中，分别是三个内角的对边，若，且.
（1）求及的值；
（2）求的值.
17. 如图，在四棱锥中，，，底面为正方形，分别为的中点．

（1）求证：平面；
（2）求直线与平面所成角正弦值．
18. 在中，角、、的对边分别是、、，且满足，，且的面积.
（1）求的值和边的值；
（2）求的值.
19. 如图，在四棱锥P—ABCD中，平面ABCD，底面ABCD是直角梯形，其中AD∥BC，，E为棱BC上的点，且
（1）求证：DE⊥平面；
（2）求二面角的余弦值；
（3）设Q为棱CP上的点（不与C、P重合），且直线QE与平面PAC所成角的正弦值为，求的值.
20. 已知函数．
（Ⅰ）求曲线在点（1，）处的切线方程；
（Ⅱ）求函数的单调区间；
（Ⅲ）已如函数，若，，不等式恒成立，求实数的取值范围．
2024-2025学年天津市河东区高三上学期第一次月考数学学情
检测试卷
一、选择题
1. 已知集合，则（ ）
A. B.
C. D.
【正确答案】C
【分析】根据集合运算的定义计算．
【详解】由题意，，
．
故选：C．
2. 设，则“”是“”的
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【正确答案】A
【详解】由，解得，由，可知“x