2024-2025学年重庆市万州区高二上册第一次月考数学质量检测试题（含解析）

这是一份2024-2025学年重庆市万州区高二上册第一次月考数学质量检测试题（含解析），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
一、单选题（本大题共8小题）
1．已知直线的倾斜角为，则直线的斜率为（ ）
A．B．C．1D．
2．已知空间向量，且，则（ ）
A．10B．6C．4D．
3．设是直线的方向向量，是平面的法向量，则（ ）
A．或B．或
C．D．
4．已知，，三点不共线，是平面外任意一点，若由确定的一点与，，三点共面，则的值为（ ）
A．B．C．D．
5．已知三点共线，则（ ）
A．B．6C．D．2
6．如图，在平行六面体中，点E，F分别为AB，的中点，则（ ）
A．B．
C．D．
7．已知，，则的最小值为（ ）
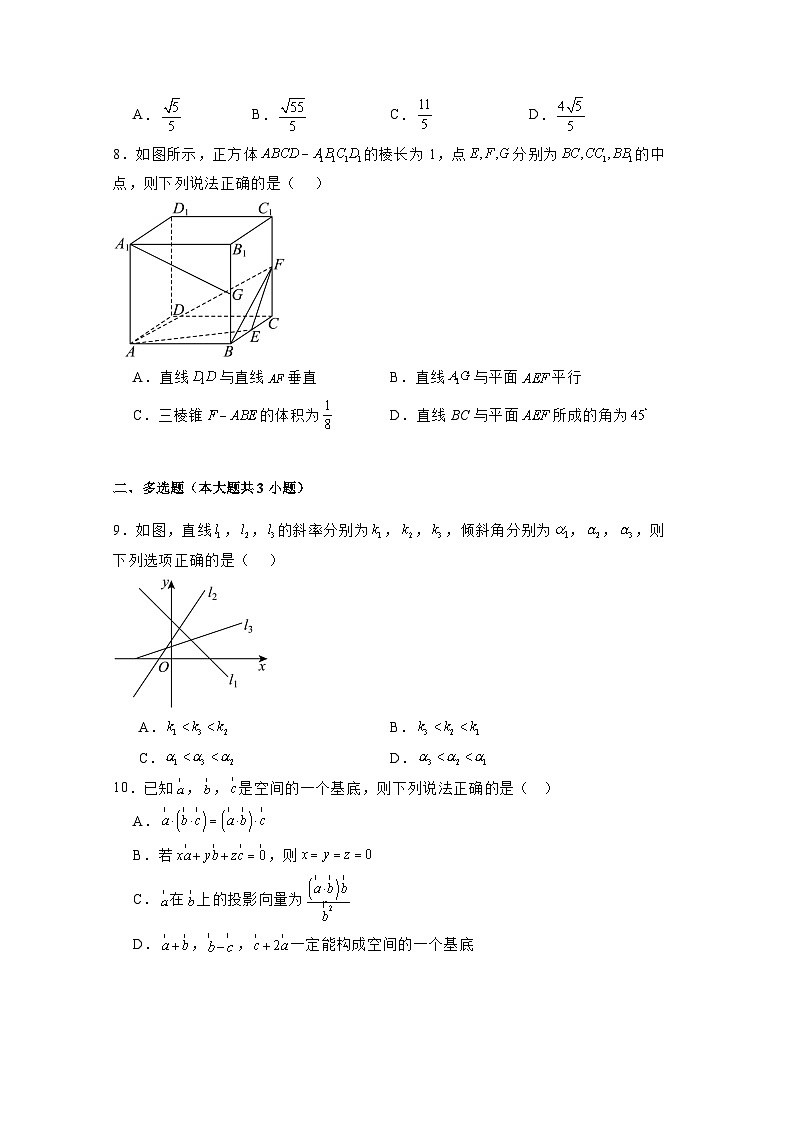
A．B．C．D．
8．如图所示，正方体的棱长为1，点分别为的中点，则下列说法正确的是（ ）
A．直线与直线垂直B．直线与平面平行
C．三棱锥的体积为D．直线BC与平面所成的角为
二、多选题（本大题共3小题）
9．如图，直线，，的斜率分别为，，，倾斜角分别为，，，则下列选项正确的是（ ）
A．B．
C．D．
10．已知，，是空间的一个基底，则下列说法正确的是（ ）
A．
B．若，则
C．在上的投影向量为
D．，，一定能构成空间的一个基底
11．如图，边长为1的正方形所在平面与正方形在平面互相垂直，动点分别在正方形对角线和上移动，且，则下列结论中正确的有（ ）
A．，使
B．线段存在最小值，最小值为
C．直线与平面所成的角恒为45°
D．，都存在过且与平面平行的平面
三、填空题（本大题共3小题）
12．点关于平面对称点是 .
13．已知空间直角坐标系中的三点、、，则点A到直线BC的距离为 ．
14．在正三棱锥中，是的中心，，则 ．
四、解答题（本大题共5小题）
15．已知直线l经过两点，同当m取何值时；
(1)直线l与x轴平行？
(2)直线l斜率不存在；
(3)直线的倾斜角为锐角？
16．如图，在平行六面体中，，.

(1)求体对角线的长度；
(2)求证：四边形为正方形.
17．如图，在多面体中，，，.侧面为矩形，平面，平面ABC，

(1)求直线与平面所成角的正弦值
(2)求直线到平面的距离.
18．如图，在四棱锥中，，，，三棱锥的体积为.
(1)求点到平面的距离；
(2)若，平面平面，点在线段上，，求平面与平面夹角的余弦值.
19．如图，已知正方形ABCD的边长为4，E，F分别为AD，BC的中点，沿EF将四边形EFCD折起，使二面角的大小为60°，点M在线段AB上.
(1)若M为AB的中点，且直线MF与直线EA的交点为O，求OA的长，并证明直线平面EMC；
(2)是否存在点M，使得直线DE与平面EMC所成的角为60°；若存在，求此时二面角的余弦值，若不存在，说明理由.
答案
1．【正确答案】C
【详解】由直线的倾斜角为，
则直线的斜率，
故选：C.
2．【正确答案】C
【分析】运用空间向量平行的坐标结论计算.
【详解】因为，所以,
即，则.
故选C.
3．【正确答案】A
【分析】依题意可得，即可得，即可判断.
【详解】因为是直线的方向向量，是平面的法向量，
所以，所以，
所以或.
故选A.
4．【正确答案】A
【详解】因为，，三点不共线，点与，，三点共面，
又，
所以，解得.
故选：A.
5．【正确答案】B
【详解】由题可得，即，解得．
故选：B
6．【正确答案】A
【分析】由空间向量的加减和数乘运算直接求解即可.
【详解】根据题意，.
故选A.
7．【正确答案】D
【详解】，
∴
，
当且仅当时取等号．
∴的最小值为．
故选：D.
8．【正确答案】B
【分析】对于A，根据正方体的性质判断；对于BD，利用空间向量判断；对于C，利用体积公式求解即可.
【详解】对于A：为正方体，所以，直线与直线不垂直，所以直线与直线不垂直，故A错误；
如图建立空间直角坐标系，则，
对于B：，
设平面的法向量为，则，
令，则，则，
因为，所以，所以，
因为在平面外，所以直线与平面平行，故B正确；
对于C：，所以三棱锥的体积为，故C错误；
对于D：，直线BC与平面所成的角为，，故D错误.
故选B.
9．【正确答案】AD
【详解】由图可得，，故A、D正确.
故选：AD.
10．【正确答案】BCD
【分析】A选项，举出反例；B选项，是空间的一个基底，故三个向量不共面且两两共面不共线，假设不全为0，推出矛盾，故假设不成立，B正确；C选项，根据投影向量公式得到C正确；D选项，推出三个向量不共面，故D正确.
【详解】A选项，当不共线时，与共线，与共线，
故不可能成立，故A不正确；
B选项，是空间的一个基底，故三个向量不共面且两两共面不共线，
假设不全为0，不妨设，此时有，故，矛盾；
不妨设，此时，故共面，矛盾；
若三者均不为0，即，此时共面，矛盾，
综上，假设不成立，故，B正确；
C选项，在上的投影向量为，C正确；
D选项，设，即，无解，
故，，不共面，一定能构成空间的一个基底，D正确.
故选：BCD
11．【正确答案】AD
【详解】因为四边形正方形，故，
而平面平面，平面平面，
平面，故平面，而平面，
故.
设，则，其中，
由题设可得，
，
对于A，当即时，，故A正确；
对于B， ，
故，当且仅当即时等号成立，故，故B错误；
对于C，由B的分析可得，
而平面的法向量为且，
故，此值不是常数，
故直线与平面所成的角不恒为定值，故C错误；
对于D，由B的分析可得，故为共面向量，
而平面，故平面，故D正确；
故选：AD
12．【正确答案】
【详解】点关于平面对称点是
故
13．【正确答案】/
【详解】依题意，，
所以点A到直线BC的距离.
故
14．【正确答案】16
【详解】如图：
首先：，.
又.
所以.
故16
15．【正确答案】(1)
(2)
(3)
【详解】（1）若直线l与x轴平行，则直线l的斜率，所以．
（2）若直线l与y轴平行，则直线l的斜率不存在，所以.
（3）由题意可知，直线l的斜率，即，解得．
16．【正确答案】(1)
(2)证明见详解
【分析】（1）根据给定条件，利用空间向量数量积的运算律求出.
（2）利用平行六面体的结构特征，结合已知及正方形的判定推理即得.
【详解】（1）在平行六面体中，，
由，，
得，
所以.
（2）在平行六面体中，，则四边形为平行四边形，
由，，得是等边三角形，即，则为菱形；
又，则，即，
所以四边形为正方形.
17．【正确答案】(1)
(2)
【详解】（1）因为侧面为矩形，
所以，
因为平面，平面，
所以，于是建立如图所示的空间直角坐标系，

，
，，，
设平面的法向量为，
，
直线与平面所成角的正弦值为；
（2）因为侧面为矩形，
所以，而平面，平面，
所以平面，
因此直线到平面的距离就是点到平面的距离，设为，
即.
18．【正确答案】(1)
(2)
【详解】（1）设点到平面的距离为，
则，
由题可知，
所以，
所以点到平面的距离为.
（2）取的中点，连接，因为，
又平面平面且交线为，平面，，
所以平面，由（1）知.
由题意可得，
所以，所以.
以点为坐标原点，为轴，为轴，过点作的平行线为轴，建立如图所示的空间直角坐标系，则，
依题意，
所以.
设平面的法向量为n1=x1,y1,z1，
则，故可设，
平面的一个法向量为，
设平面与平面的夹角为，
则，
所以平面与平面夹角的余弦值为.
19．【正确答案】(1)；证明见解析；
(2)存在点，使得直线与平面所成的角为；此时二面角的余弦值为.
【详解】（1）分别为中点，
，且，
又为中点，且，
易得，
连接，交于点，连接，
由题设，易知四边形为平行四边形，
为中点，
是的中点，
为中点，
，又平面，平面，
平面；
（2），
，，
又平面，平面，
即为二面角的平面角，
；
取中点，连接，如图，
，，
，
，
，
，
，，又平面，，
平面，
平面，
，
则以为坐标原点，方向为轴正方向建立空间直角坐标系如下图所示，
则，，，，
设，则，，，
设平面的法向量n1=x1,y1,z1，则，
令，则，，，
直线与平面所成的角为，
，解得或，
存在点，当或时，使得直线与平面所成的角为；
设平面的法向量，又，，
，
令，则，，；
当时，，；
当时，，；
综上所述：二面角的余弦值为.