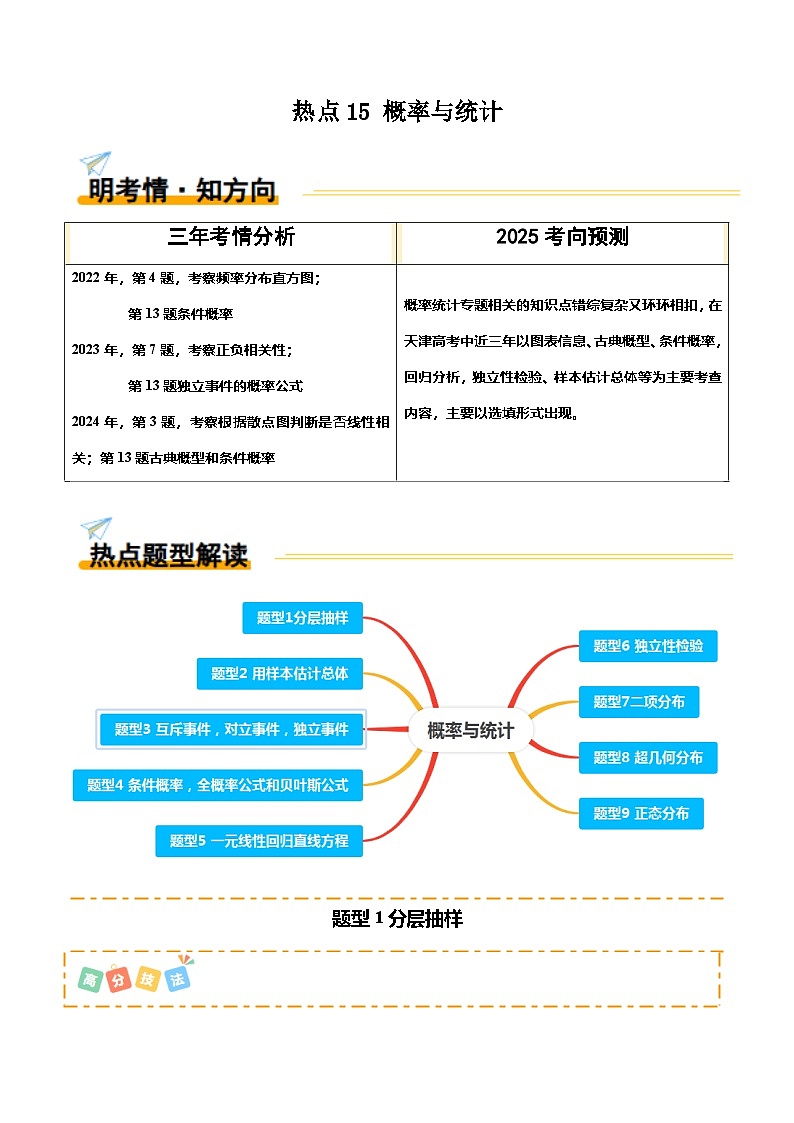
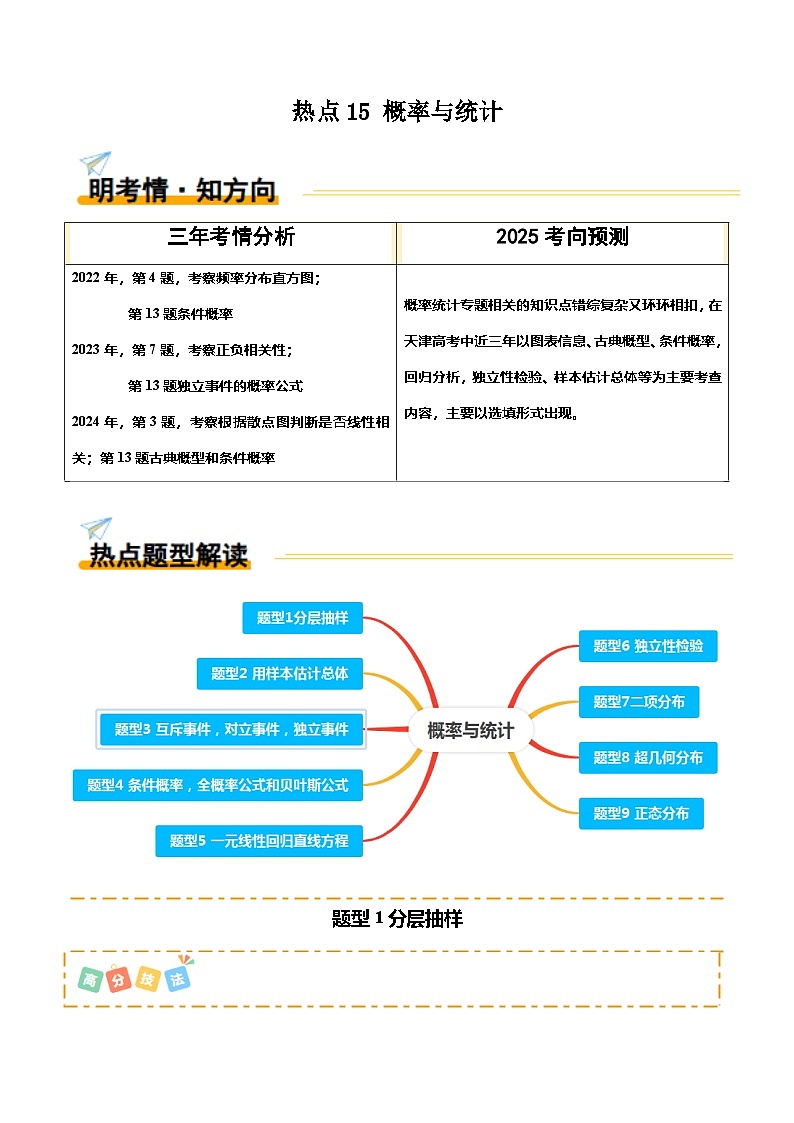
热点15 概率与统计（9题型 高分技法 限时提升练）-2025年高考数学 热点 重点 难点 专练（天津专用）

这是一份热点15 概率与统计（9题型 高分技法 限时提升练）-2025年高考数学 热点 重点 难点 专练（天津专用），文件包含热点15概率与统计9题型高分技法限时提升练-2025年高考数学热点重点难点专练天津专用原卷版docx、热点15概率与统计9题型高分技法限时提升练-2025年高考数学热点重点难点专练天津专用解析版docx等2份试卷配套教学资源，其中试卷共78页， 欢迎下载使用。

题型1分层抽样
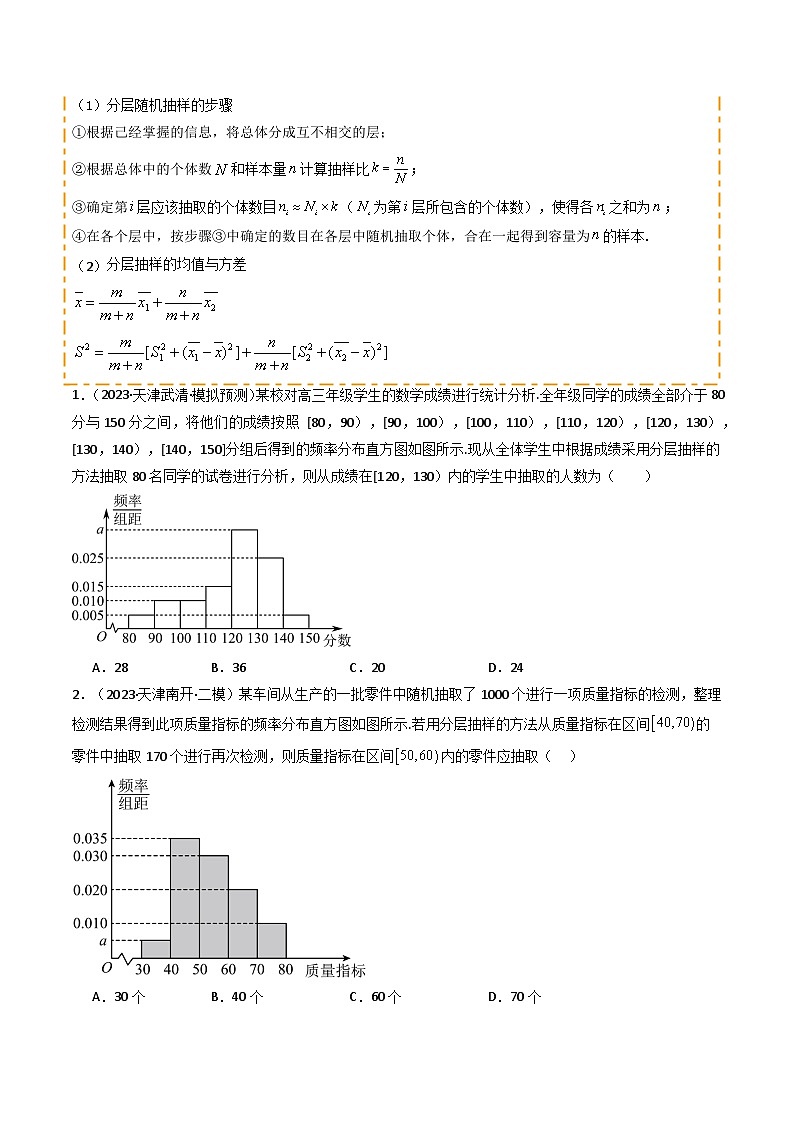
1．（2023·天津武清·模拟预测）某校对高三年级学生的数学成绩进行统计分析.全年级同学的成绩全部介于80分与150分之间，将他们的成绩按照 [80，90），[90，100），[100，110），[110，120），[120，130），[130，140），[140，150]分组后得到的频率分布直方图如图所示.现从全体学生中根据成绩采用分层抽样的方法抽取80名同学的试卷进行分析，则从成绩在[120，130）内的学生中抽取的人数为（ ）

A．28B．36C．20D．24
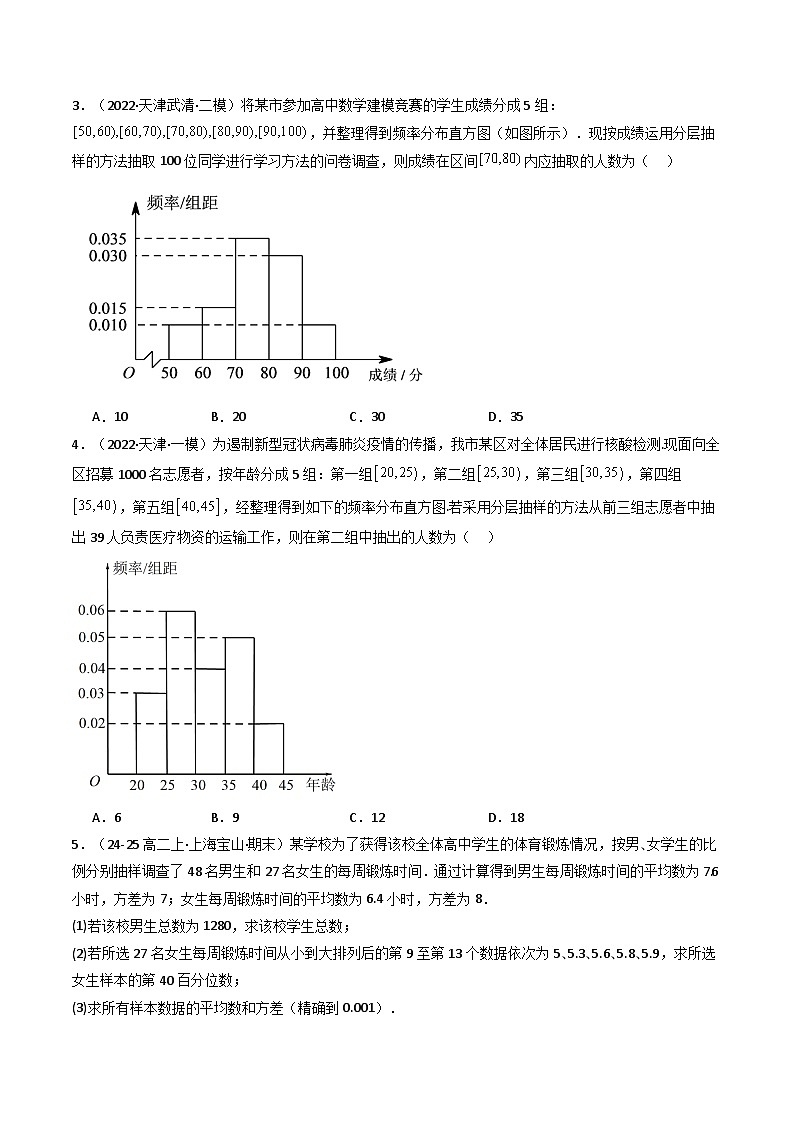
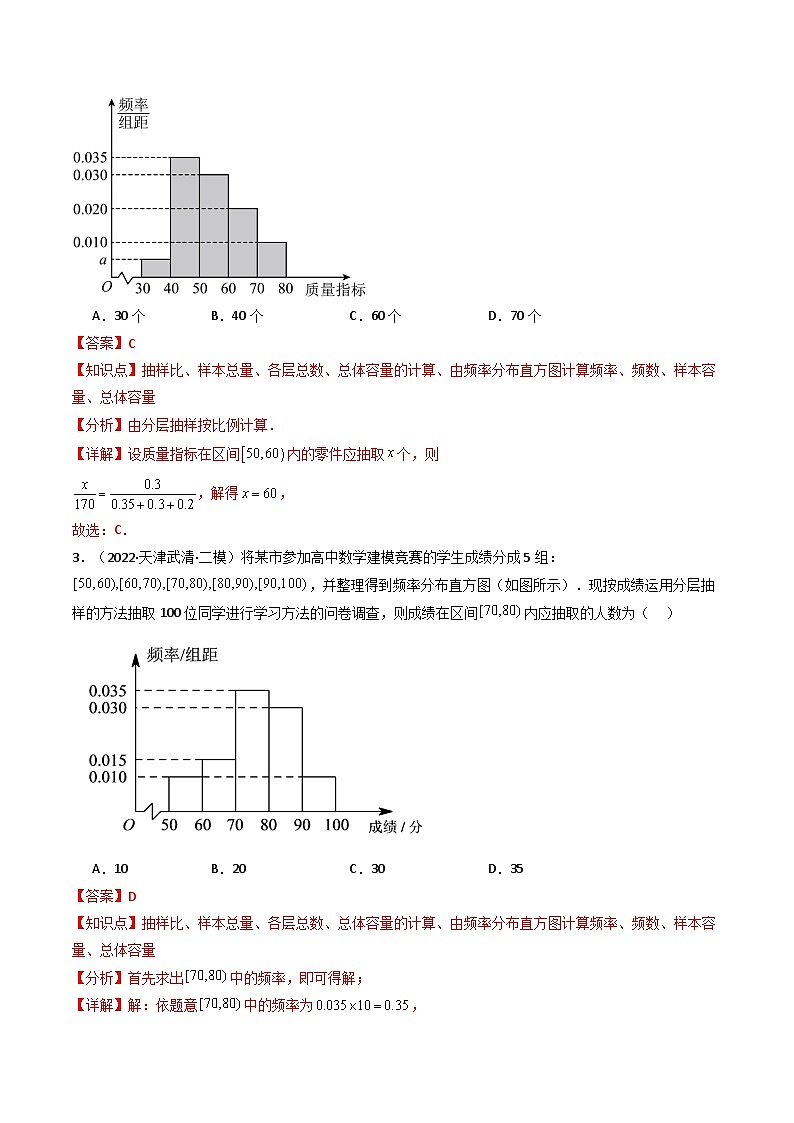
2．（2023·天津南开·二模）某车间从生产的一批零件中随机抽取了1000个进行一项质量指标的检测，整理检测结果得到此项质量指标的频率分布直方图如图所示.若用分层抽样的方法从质量指标在区间的零件中抽取170个进行再次检测，则质量指标在区间内的零件应抽取（ ）
A．30个B．40个C．60个D．70个
3．（2022·天津武清·二模）将某市参加高中数学建模竞赛的学生成绩分成5组：，并整理得到频率分布直方图（如图所示）．现按成绩运用分层抽样的方法抽取100位同学进行学习方法的问卷调查，则成绩在区间内应抽取的人数为（ ）
A．10B．20C．30D．35
4．（2022·天津·一模）为遏制新型冠状病毒肺炎疫情的传播，我市某区对全体居民进行核酸检测.现面向全区招募1000名志愿者，按年龄分成5组：第一组，第二组，第三组，第四组，第五组，经整理得到如下的频率分布直方图.若采用分层抽样的方法从前三组志愿者中抽出39人负责医疗物资的运输工作，则在第二组中抽出的人数为（ ）
A．6B．9C．12D．18
5．（24-25高二上·上海宝山·期末）某学校为了获得该校全体高中学生的体育锻炼情况，按男､女学生的比例分别抽样调查了48名男生和27名女生的每周锻炼时间．通过计算得到男生每周锻炼时间的平均数为7.6小时，方差为7；女生每周锻炼时间的平均数为6.4小时，方差为8．
(1)若该校男生总数为1280，求该校学生总数；
(2)若所选27名女生每周锻炼时间从小到大排列后的第9至第13个数据依次为5､5.3､5.6､5.8､5.9，求所选女生样本的第40百分位数；
(3)求所有样本数据的平均数和方差（精确到0.001）．
6．（2024·上海青浦·一模）第七届中国国际进口博览会于 2024 年 11 月 5 日至 10 日在上海举办，某公司生产的 、 三款产品在博览会上亮相，每一种产品均有普通装和精品装两种款式，该公司每天产量如下表: （单位:个）
现采用分层抽样的方法在某一天生产的产品中抽取 100 个，其中 款产品有30 个.
(1)求 的值；
(2)用分层抽样的方法在 款产品中抽取一个容量为5的样本，从样本中任取 2 个产品，求其中至少有一个精品装产品的概率;
(3)对抽取到的 款产品样本中某种指标进行统计，普通装产品的平均数为10，方差为2， 精品装产品的平均数为12，方差为1.8，试估计这天生产的 款产品的某种指标的总体方差 （精确到 0.01 ）.
7．（24-25高一上·辽宁沈阳·期末）某医疗单位为了迎接医师节，针对本单位不同年龄的员工举办了一次实践技能大比拼活动，满分100分（95分及以上为优秀医师），共有100人荣获“优秀医师”称号，将其按年龄分成以下五组：第一组，第二组，第三组，第四组，第五组，得到如图所示的频率分布直方图.
(1)根据频率分布直方图，估计这些人的平均年龄；
(2)若从第三组，第四组，第五组三组中分层抽取6人，再从这6人中随机抽取2人，求抽取的2人年龄在不同组的概率；
(3)若第四组的年龄的平均数与方差分别为54和1，第五组的年龄的平均数与方差分别为66和4，据此计算这100人中第四组与第五组所有人的年龄的方差.
附：
题型2 用样本估计总体
1．（2024·天津河西·二模）某校高三年级举行数学知识竞赛，并将100名学生的竞赛成绩（满分100分，成绩取整数）整理成如图所示的频率分布直方图，则估计这组数据的第85百分位数为（ ）
A．85B．86C．86.5D．87
2．（2024·天津·二模）为了加深师生对党史的了解，激发广大师生知史爱党、知史爱国的热情，某校举办了“学党史、育文化”的党史知识竞赛，并将1000名师生的竞赛成绩（满分100分，成绩取整数）整理成如图所示的频率分布直方图，估计这组数据的第85百分位数为（ ）分
A．84B．85C．86D．87
3．（2024·天津·二模）为深入贯彻落实习近平总书记对天津工作“三个着力”重要要求，天津持续深化改革，创建全国文明城区，城市文明程度显著提升，人民群众的梦想不断实现.在创建文明城区的过程中，中央文明办对某小区居民进行了创建文明城区相关知识网络问卷调查，从本次问卷中随机抽取了50名居民的问卷结果，统计其得分数据，将所得50份数据的得分结果分为6组：，并整理得到如下的频率分布直方图，则该小区居民得分的第70百分位数为（ ）

A．89.09B．86.52C．84.55D．81.32
4．（2024·天津·二模）某校举办了数学知识竞赛，把1000名学生的竞赛成绩（满分100分，成绩取整数）按，，，分成四组，并整理成如图所示的频率分布直方图，则下列说法正确的为（ ）
A．的值为0.015B．估计这组数据的众数为80
C．估计这组数据的第60百分位数为87D．估计成绩低于80分的有350人
5．（2024·天津河北·一模）已知甲乙两组数据分别为和，则下列说法中不正确的是（ ）
A．甲组数据中第70百分位数为23B．甲乙两组数据的极差相同
C．乙组数据的中位数为25.5D．甲乙两组数据的方差相同
6．（2023·天津和平·二模）一组样本数据的频率分布直方图如图所示，试估计此样本数据的中位数为（ ）

A．13B．12C．D．
7．（2023·天津滨海新·三模）为了解学生每天的体育活动时间，某市教育部门对全市高中学生进行调查，随机抽取1000名学生每天进行体育运动的时间，按照时长（单位：分钟）分成6组：第一组，第二组，第三组，第四组，第五组，第六组．对统计数据整理得到如图所示的频率分布直方图，则下列结论不正确的是（ ）

A．频率分布直方图中的
B．估计1000名学生每天体育活动不少于一个小时的学生人数为400
C．估计1000名学生每天体育活动时间的众数是55
D．估计1000名学生每天体育活动时间的第25百分位数为
8．（2023·天津北辰·三模）少年强则国强，少年智则国智．党和政府一直重视青少年的健康成长，出台了一系列政策和行动计划，提高学生身体素质．为了加强对学生的营养健康监测，某校在3000名学生中，抽查了100名学生的体重数据情况．根据所得数据绘制样本的频率分布直方图如图所示，则下列结论正确的是（ ）
A．样本的众数为65B．样本的第80百分位数为72.5
C．样本的平均值为67.5D．该校学生中低于的学生大约为1000人
题型3 互斥事件，对立事件，独立事件
1．（23-24高一下·天津·期末）一个质地均匀的正四面体木块的四个面上分别标有数字1，2，3，4.连续抛掷这个正四面体木块两次，并记录每次正四面体木块朝下的面上的数字，记事件A为“第一次向下的数字为2或3”，事件为“两次向下的数字之和为奇数”，则下列结论正确的是（ ）
A．B．事件与事件互斥
C．事件与事件相互独立D．
2．（2024·上海嘉定·一模）假定生男生女是等可能的，设事件：一个家庭中既有男孩又有女孩；事件家庭中最多有一个女孩.针对下列两种情形：①家庭中有2个小孩；②家庭中有3个小孩，下面说法正确是（ ）.
A．①中事件与事件相互独立､②中的事件与事件相互独立
B．①中事件与事件不相互独立､②中的事件与事件相互独立
C．①中事件与事件相互独立､②中的事件与事件不相互独立
D．①中事件与事件不相互独立､②中的事件与事件不相互独立
3．（2024·上海虹口·一模）已知事件和事件满足，则下列说法正确的是（ ）．
A．事件和事件独立B．事件和事件互斥
C．事件和事件对立D．事件和事件互斥
4．（2024·广东广州·模拟预测）掷出两枚质地均匀的骰子，记事件“第一枚点数小于3”，事件“第二枚点数大于4”，则与关系为（ ）
A．互斥B．互为对立C．相互独立D．相等
5．（23-24高一下·天津·期末）一个袋子中有大小和质地相同的4个球，其中有2个红色球（标号为1和2），2个黑色球（标号为3和4），采用不放回简单随机抽样的方法从袋中依次摸出2个球．设事件“摸到的2个球颜色不相同”，事件“摸到的2个球的数字之和大于5”．
(1)用集合的形式写出试验的样本空间，并求，；
(2)求，并说明事件与是否相互独立．
题型4 条件概率，全概率公式和贝叶斯公式
1．（2024·天津北辰·三模）某单位为了提高员工身体素质，开展双人投篮比寒，现甲、乙两人为一组参加比赛， 每次由其中一人投篮，规则如下:若投中，则此人继续投篮，若未投中，则换为对方投篮，无论之前投篮的情况如何，甲每次投篮的命中率均为，乙每次投篮的命中率均为.由抽签确定第1次投篮的人选，第1次投篮的人是甲、乙的概率各为.第2次投篮的人是甲的概率为 ；已知在第2次投篮的人是乙的情况下，第1次投篮的人是甲的概率为 .
2．（2024·天津河西·模拟预测）甲、乙、丙三个人去做相互传球训练，训练规则是确定一人第一次将球传出，每次传球时，传球者都等可能地将球传给另外两个人中的任何一人，每次必须将球传出．如果第一次由甲将球传出，设次传球后球在甲手中的概率为，则 ； ．
3．（2024·天津北辰·模拟预测）甲和乙两个箱子中各装有5个大小相同的小球，其中甲箱中有3个红球、2个白球，乙箱中有4个红球、1个白球，从甲箱中随机抽出2个球，在已知至少抽到一个红球的条件下，则2个球都是红球的概率为 ；掷一枚质地均匀的骰子，如果点数小于等于4，从甲箱子中随机抽出1个球；如果点数大于等于5，从乙箱子中随机抽出1个球，若抽到的是红球，则它是来自乙箱的概率是 .
4．（2024·天津河北·二模）学习小组为了研究手机对学生学习的影响，对本学校学生手机使用情况统计分析有以下结果：若学生前一天没有玩手机，则接下来一天也不玩手机的概率为0.7，若学生前一天玩手机，接下来一天也玩手机的概率为0.8. 已知一个学生第一天没玩手机，根据这个统计结果计算，那么他第二天玩手机的概率为 ，第三天不玩手机的概率为 .
5．（2023·天津和平·三模）抛掷两颗质地均匀的骰子，其中白色骰子与黑色骰子各一颗，记事件为“白色骰子的点数为或”，事件为“两颗骰子点数之和大于”，则 ； ．
6．（2024·天津滨海新·三模）随着我国经济发展越来越好，外出旅游的人越来越多，现有两位游客慕名来天津旅游，他们分别从天津之眼摩天轮、五大道风景区、古文化街、意式风情街、海河观光游船、盘山风景区，这6个随机选择1个景点游玩，两位游客都选择天津之眼摩天轮的概率为 ．这两位游客中至少有一人选择天津之眼摩天轮的条件下，他们选择的景点不相同的概率 ．
7．（2024·天津河西·模拟预测）甲、乙两名同学在电脑上进行答题测试，每套测试题可从题库中随机抽取.在一轮答题中，如果甲单独答题，能够通过测试的概率是，如果乙单独答题，能够通过测试的概率是.若甲单独答题三轮，则甲恰有两轮通过测试的概率为 ；若在甲，乙两人中任选一人进行测试，则通过测试的概率为 .（结果均以既约分数表示）
8．（2024·天津·二模）为缓解高三学习压力，某高中校举办一对一石头、剪刀、布猜拳比赛，比赛约定赛制如下：累计赢2局者胜，分出胜负即停止比赛；若猜拳4局仍未分出胜负，则比赛结束. 在一局猜拳比赛中，已知每位同学赢､输､平局的概率均为，每局比赛的结果相互独立. 现甲、乙两位同学对战，则甲同学比赛三局获胜的概率为 ；已知比赛进行了四局的前提下，两位选手未分出胜负的概率为 .
题型5 一元线性回归直线方程
1．（2024·天津河北·二模）云计算是信息技术发展的集中体现，近年来，我国云计算市场规模持续增长. 已知某科技公司2018年至2022年云计算市场规模数据，且市场规模与年份代码的关系可以用模型（其中为自然对数的底数）拟合，设，得到数据统计表如下：
由上表可得经验回归方程，则2026年该科技公司云计算市场规模的估计值为（ ）
（参考公式：）
A．B．C．D．
2．（2024·天津·二模）有人通过调查统计发现，儿子成年时的身高与父亲的身高呈线性相关，且儿子成年时的身高（单位：）与父亲的身高（单位：）的经验回归方程为，根据以上信息，下列判断正确的为（ ）．
A．儿子成年时的身高与父亲的身高的样本相关系数
B．父亲的身高为，儿子成年时的身高一定在到之间
C．父亲的身高每增加，儿子成年时的身高平均增加
D．儿子在成年时的身高一般会比父亲高
3．（2024·天津·一模）已知变量x和y满足经验回归方程，且变量x和y之间的一组相关数据如表所示，则下列说法错误的是（ ）
A．变量x和y呈负相关B．当时，
C．D．该经验回归直线必过点
4．（2024·天津河西·一模）随着居民家庭收入的不断提高，人们对居住条件的改善的需求也在逐渐升温．某城市统计了最近5个月的房屋交易量，如下表所示：
若与满足一元线性回归模型，且经验回归方程为，则下列说法错误的是（ ）
A．根据表中数据可知，变量与正相关
B．经验回归方程中
C．可以预测时房屋交易量约为（万套）
D．时，残差为
5．（2023·天津河西·三模）某产品的广告费用x与销售额y的统计数据如下表：
根据上表可得回归方程的约等于9，据此模型预报广告费用为6万元时，销售额约为（ ）
A．56万元B．57万元C．58万元D．59万元
题型6 独立性检验
1．（2024·天津·模拟预测）下列说法正确的序号是（ ）
①在回归直线方程中，当解释变量x每增加一个单位时，预报变量平均增加0.8个单位；
②利用最小二乘法求回归直线方程，就是使得最小的原理；
③已知X，Y是两个分类变量，若它们的随机变量的观测值k越大，则“X与Y有关系”的把握程度越小；
④已知随机变量服从正态分布，且，则.
A．①②③B．②③④C．②④D．①②④
2．（23-24高二下·天津·期末）为考察某种药物对预防疾病的效果，进行了动物试验，根据40个有放回简单随机样本的数据，得到如下列联表：
(1)补全下面的列联表（单位：只）；
(2)依据的独立性检验，分析药物对预防疾病的有效性.
参考公式：，其中.
参考附表：
3．（23-24高二下·天津河西·期中）某班主任对班级22名学生进行了作业量多少的调查，数据如下：在喜欢玩电脑游戏的12人中，有9人认为作业多，3人认为作业不多；在不喜欢玩电脑游戏的10人中，有4人认为作业多，6人认为作业不多．
(1)根据以上数据填写2×2列联表；
(2)依据小概率的独立性检验，分析喜欢玩电脑游戏与认为作业多少是否有关系？
参考公式：，
参考数据：,
．
4．（2024·西藏拉萨·一模）某社区组织居民开在垃圾分类知识竞赛活动.随机对该社区名居民的成绩进行统计，成绩均在内，将成绩分成组进行统计分析：第组有人，第组有16人，第组有人，第组有人，第组有人.现使用分层随机抽样的方法在第，组共选取人参加垃圾分类志愿者工作.
(1)对该社区名居民进行问卷调查，部分数据如下表所示，补全表格数据，并依据小概率值的独立性检验，分析能否认为居民喜欢垃圾分类与性别有关；
(2)若从参加垃圾分类志愿者工作的人中随机选取人参加垃圾分类知识宣讲工作，记来自第组的人数为，求的分布列及数学期望.
附：，.
5．（2024·广东佛山·一模）某机构为了解市民对交通的满意度，随机抽取了100位市民进行调查，结果如下：回答“满意”的人数占总人数的一半，在回答“满意”的人中，“上班族”的人数是“非上班族”人数的；在回答“不满意”的人中，“非上班族”占．
(1)请根据以上数据填写下面列联表，并依据小概率值的独立性检验，分析能否认为市民对于交通的满意度与是否上班存在关联？
(2)该机构欲再从全市随机选取市民，进一步征求改善交通现状的建议．规定：抽样的次数不超过6次，若随机抽取的市民属于不满意群体，则抽样结束；若随机抽取的市民属于满意群体，则继续抽样，直到抽到不满意市民或抽样次数达到6次时，抽样结束．以调查数据中的满意度估计全市市民的满意度，求抽样次数的分布列和数学期望．
附：
参考公式：，其中．
题型7二项分布
1．（2023·天津南开·二模）一个盒子中装有5个电子产品，其中有3个一等品，2个二等品，从中每次抽取1个产品.若抽取后不再放回，则抽取三次，第三次才取得一等品的概率为 ；若抽取后再放回，共抽取10次，则平均取得一等品 次.
2．（2023·天津·二模）某篮球队对队员进行考核，规则是①每人进行5个轮次的投篮；②每个轮次每人投篮2次，若至少投中1次，则本轮通过，否则不通过.已知队员甲投篮1次投中的概率为0.6，如果甲各次投篮投中与否互不影响，那么甲第一轮通过的概率为 ；甲5个轮次通过的次数的期望是 .
3．（2023·天津和平·二模）在学校大课间体育活动中，甲､乙两位同学进行定点投篮比赛，每局比赛甲､乙每人各投篮一次，若一方命中且另一方末命中，则命中的一方本局比赛获胜，否则为平局．已知甲､乙每次投篮命中的概率分别为和，且每局比赛甲､乙命中与否互不影响，各局比赛也互不影响．则进行1局投篮比赛，甲､乙平局的概率为 ；设共进行了10局投篮比赛，其中甲获胜的局数为，求的数学期望 ．
4．（2022·天津·二模）某电视台招聘节目主持人，应聘者需进行笔试和面试两个环节，若两个环节都合格，则可以成为该电视台的节目主持人.已知甲、乙、丙三人同时参加应聘，三人笔试合格的概率依次为0.5，0.4，0.6，面试合格的概率依次为0.6，0.75，0.5，且每个人在两个环节中是否合格互不影响，甲、乙、丙也互不影响，则甲、乙、丙三人在笔试中恰有一人合格的概率为 ；记甲、乙、丙三人在本次应聘中成为电视台的节目主持人的人数为，则随机变量的期望为 .
5．（23-24高二下·天津北辰·阶段练习）某学校有，两家餐厅，经统计发现，某班学生第1天午餐时选择餐厅和选择餐的概率均为.如果第1天去餐厅，那么第2天去餐厅的概率为；如果第1天去餐厅，那么第2天去餐厅的概率为，则某同学第2天去餐厅用餐的概率为 ；假设班内各位同学的选择相互独立，随机变量为该班3名同学中第2天选择餐厅的人数，则随机变量的均值 .
题型8 超几何分布
1．（2024·天津·二模）盒子里有大小和形状完全相同的4个黑球和6个红球，每次从中随机取一个球，取后不放回．在第一次取到黑球的条件下，第二次取到黑球的概率是 ；若连续取2次球，设随机变量表示取到的黑球个数，则 ．
2．（2023·天津·三模）现有4个红球和4个黄球，将其分配到甲、乙两个盒子中，每个盒子中4个球．甲盒子中有2个红球和2个黄球的概率为 ；甲盒子中有3个红球和1个黄球，若同时从甲、乙两个盒子中取出个球进行交换，记交换后甲盒子中的红球个数为，的数学期望为，则 ．
3．（2022·天津武清·模拟预测）某校高三年级有男生360人，女生240人，对高三学生进行问卷调查，采用分层抽样的方法，从这600名学生中抽取5人进行问卷调查，再从这5名学生中随机抽取3人进行数据分析，则这3人中既有男生又有女生的概率是 ，记抽取的男生人数为，则随机变量的数学期望为 ．
4．（2022·天津滨海新·三模）甲箱中有5个红球，2个白球和3个黑球，乙箱中有4个红球，3个白球和3个黑球．先从甲箱中随机取出1球放入乙箱中，分别以、、表示由甲箱中取出的是红球，白球和黑球的事件；再从乙箱中随机取出一球，以表示由乙箱中取出的球是红球的事件，则 ；若随机从甲箱中取出3个球，设取到红球个数为随机变量X，则X的数学期望为 ．
5．（2024·河南·模拟预测）某校组织建国75周年知识竞赛，在决赛环节，每名参赛选手从答题箱内随机一次性抽取2个标签.已知答题箱内放着写有类题目的标签4个，类题目的标签4个，类题目的标签2个，每个标签上写有一道不同的题目，且标签的其他特征完全相同.
(1)求选手抽取的2个标签上的题目类型不相同的概率；
(2)设抽取到写有类题目的标签的个数为，求的分布列和数学期望.
题型9 正态分布
1．（2023·天津红桥·一模）某班级有50名学生，期末考试数学成绩服从正态分布，已，则的学生人数为（ ）
A．5B．10C．20D．30
2．（2024·天津南开·一模）已知随机变量，且，则（ ）
A．B．C．D．
3．（2023·天津和平·三模）①一组数据的第三四分位数为8；
②若随机变量，且，则；
③具有线性相关关系的变量，其线性回归方程为，若样本的中心，则；
④如图，现要用5种不同的颜色对某市的4个区县地图进行着色，要求有公共边的两个地区不能用同一种颜色，共有180种不同的着色方法.
以上说法正确的个数为（ ）
A．1个B．2个C．3个D．4个
4．（2024·江苏扬州·模拟预测）已知随机变量，且，则的值为（ ）
A．B．
C．D．
5．（2024·重庆·模拟预测）某中学为提升学生们的数学素养，激发大家学习数学的兴趣，举办了一场“数学文化素养知识大赛”，分为初赛和复赛两个环节，初赛成绩排名前两百名的学生参加复赛．已知共有8000名学生参加了初赛，现从参加初赛的全体学生中随机地抽取100人的初赛成绩作为样本，得到如下频率分布直方图：

(1)规定初赛成绩中不低于90分为优秀，8090分为良好，7080分为一般，6070分为合格，60分以下为不合格，若从上述样本中初赛成绩不低于80分的学生中随机抽取2人，求至少有1人初赛成绩优秀的概率，并求初赛成绩优秀的人数的分布列及数学期望；
(2)由频率分布直方图可认为该校全体参加初赛学生的初赛成绩服从正态分布，其中可近似为样本中的100名学生初赛成绩的平均值（同一组数据用该组区间的中点值代替），且．已知小华的初赛成绩为85分，利用该正态分布，估计小华是否有资格参加复赛？
（参考数据：；若，则，，．
（建议用时：60分钟）
一、单选题
1．（2024·天津和平·一模）某市为了减少水资源浪费，计划对居民生活用水实施阶梯水价制度，为确定一个比较合理的标准，从该市随机调查了100位居民，获得了他们某月的用水量数据，整理得到如下频率分布直方图，则以下四个说法正确的个数为（ ）

①估计居民月均用水量低于的概率为0.25；②估计居民月均用水量的中位数约为；③该市有40万居民，估计全市居民中月均用水量不低于的人数为6万；④根据这100位居民的用水量，采用样本量按比例分配的分层随机抽样的方法，抽取了容量为20人的样本，则在用水量区间中应抽取4人.
A．1B．2C．3D．4
2．（2024·天津河东·二模）下列说法中正确的是（ ）
A．具有线性相关关系的变量，，其线性回归方程为，若样本的中心，则
B．数据3，4，2，8，1，5，8，6的中位数为5
C．将一组数据中的每一个数据加上同一个正数后，方差变大
D．若甲、乙两组数据的相关系数分别为和0.89，则甲组数据的线性相关性更强
3．（2024·天津滨海新·三模）下列说法中正确的是（ ）
A．一组数据3，4，2，8，1，5，8，6，9，9，的第60百分位数为6
B．将一组数据中的每一个数据加上同一个正数后，方差变大
C．若甲、乙两组数据的相关系数分别为和，则甲组数据的线性相关程度更强
D．在一个列联表中，由计算得的值，则的值越接近1，判断两个变量有关的把握越大
4．（2024·天津武清·模拟预测）某校高三共有200人参加体育测试，将体测得分情况进行了统计，把得分数据按照分成6组，绘制了如图所示的频率分布直方图.根据规则，82分以上的考生成绩等级为A，则获得的考生人数约为（ ）
A．25B．50C．75D．100
5．（2024·天津·三模）按从小到大顺序排列的两组数据：甲组：7，11，14，m，22；乙组：5，10，n，18，20，若这两组数据的第50百分位数、第80百分位数分别对应相等，则=（ ）
A．28B．29C．30D．32
6．（23-24高三上·天津北辰·期中）下列结论中，错误的是（ ）
A．数据4，1，6，2，9，5，8的第60百分位数为6
B．若随机变量，则
C．已知经验回归方程为，且，则
D．根据分类变量与成对样本数据，计算得到χ2=9.632，依据小概率值的独立性检验，可判断与有关联，此推断犯错误的概率不大于0.001
7．（2024·天津北辰·模拟预测）下列命题中，不正确的是（ ）
A．若随机变量，则
B．若随机变量，且，则
C．若x>0，，则的最小值为
D．两个随机变量的相关系数越大，两个变量的线性相关性越强
8．（2023·天津和平·三模）下列说法中，正确的个数为（ ）
①样本相关系数的绝对值大小可以反映成对样本数据之间线性相关的程度；
②用不同的模型拟合同一组数据，则残差平方和越小的模型拟合的效果越好；
③随机变量服从正态分布，若，则；
④随机变量服从二项分布，若方差，则．
A．1个B．2个C．3个D．4个
9．（2024·天津·一模）下列说法正确的是（ ）
A．一组数据的第80百分位数为17；
B．根据分类变量与的成对样本数据，计算得到，根据小概率值的独立性检验，可判断与有关联，此推断犯错误的概率不大于0.05；
C．两个随机变量的线性相关性越强，相关系数的绝对值越接近于0；
D．若随机变量满足，则．
二、填空题
10．（2022·天津滨海新·模拟预测）为了抗击新冠肺炎疫情，现在从甲医院200人和乙医院100人中，按分层抽样的方法，选出6人加入“援鄂医疗队”，再从此6人中选出3人作为联络员，则这3名联络员中甲乙两所医院均有人员入选的条件下，恰有2人来自乙医院的概率是 ．设3名联络员中甲医院的人数为，则随机变量的数学期望为 ．
11．（2024·天津和平·二模）为铭记历史、缅怀先烈，增强爱国主义情怀，某学校开展共青团知识竞赛活动．在最后一轮晋级比赛中，甲、乙、丙三名同学回答一道有关团史的问题，每个人回答正确与否互不影响．已知甲回答正确的概率为，甲、丙两人都回答正确的概率是，乙、丙两人都回答正确的概率是．若规定三名同学都回答这个问题，则甲、乙、丙三名同学中至少有1人回答正确的概率为 ；若规定三名同学抢答这个问题，已知甲、乙、丙抢到答题机会的概率分别为，，，则这个问题回答正确的概率为 ．
12．（2024·天津·模拟预测）一个袋子中有10个大小相同的球，其中红球7个，黑球3个.每次从袋中随机摸出1个球，摸出的球不再放回.设第1，2，3次都摸到红球的概率为；在第1，2次都摸到红球的条件下，第3次摸到红球的概率为.求 .
13．（2024·天津武清·模拟预测）某学校为普及垃圾分类知识，增强学生的垃圾分类意识，在全校范围内举办垃圾分类知识竞赛.通过选拔，仅有甲、乙两名选手进入决赛.决赛采用积分制，规则为:抢答3道题，每题10分，答对得10分，答错自己不得分，对方得10分.选手是否抢到试题是等可能的，且回答对错互不影响，得分高的获胜.已知甲、乙两名选手答对每道题的概率分别为，记事件A为“答第一道题，甲选手得分”，则 ，记甲选手的得分为（单位，分）， ．
14．（2024·天津·模拟预测）某班从6名班干部（其中男生4人，女生2人）中，任选3人参加学校的义务劳动.男生甲或女生乙被选中的概率为 ；设“男生甲被选中”为事件，“女生乙被选中”为事件，则 .
15．（2024·天津·一模）甲和乙两个箱子中各装有4个大小相同的小球，其中甲箱中有2个红球、2个白球，乙箱中有3个红球、1个白球，从甲箱中随机抽出2个球，在已知抽到白球的条件下，则2个球都是白球的概率为 ；掷一枚质地均匀的骰子，如果点数小于等于2，就从甲箱子中随机抽出1个球；如果点数大于等于3，就从乙箱子中随机抽出1个球，则抽到红球的概率为 .
三、解答题
16．（2024·全国·模拟预测）某校高一学生共有人，年级组长利用数字化学习软件记录每位学生每日课后作业完成的时长，期中考试之后统计得到了如下平均作业时长与学业成绩的数据表：
(1)试判断：是否有的把握认为学业成绩优秀与日均作业时长不小于小时且小于小时有关？
(2)常用表示在事件发生的条件下事件发生的优势，在统计中称为似然比．已知该校高一学生女生中成绩优秀的学生占比，现从所有高一学生中任选一人，表示“选到的是男生”，表示“选到的学生成绩优秀”，若，求．
附：，．
17．（24-25高三上·上海奉贤·期中）某市数学竞赛初赛结束后，为了解竞赛成绩情况，从所有学生中随机抽取名学生，得到他们的成绩，将数据分成五组：，，，，，并绘制成如图所示的频率分布直方图：
(1)若只有前的学生能进决赛，则入围分数应设为多少分？
(2)采用分层随机抽样的方法从成绩为的学生中抽取容量为的样本，再从该样本中随机抽取名学生进行问卷调查，设为其中达到分及以上的学生的人数，求的概率分布及数学期望.
18．（2024·广东·二模）某市举办一年一度的风筝节，吸引大批游客前来观赏.为了解交通状况，有关部门随机抽取了200位游客，对其出行方式进行了问卷调查（每位游客只填写一种出行方式），具体情况如下：
用上表样本的频率估计概率，低碳出行方式包括地铁、公交车、骑行和步行：
(1)若从参加活动的所有游客中随机抽取3人，这3人中低碳出行的人数记为，求和；
(2)据另一项调查显示，80%的低碳出行的游客表示明年将继续参加活动，60%的非低碳出行的游客表示明年将继续参加活动，求今年参加活动的游客明年继续参加活动的概率.
19．（2022·安徽马鞍山·模拟预测）某市对全市高二学生的4月数学期中测试成绩（满分150分）进行数据统计发现：数学成绩X近似服从正态分布．现从甲、乙两校100分以上的试卷中分别抽取了15份试卷进行分析，将得到的30份试卷的成绩制成茎叶图如下：
(1)根据茎叶图，求甲、乙两校所抽取的试卷的成绩的中位数与，并判断方差，的大小（只需写出结果）；
(2)在这30份试卷中，从成绩在140分以上的试卷中任意抽取3份，将这3份试卷中成绩在全市前0.15%的份数记为，求的分布列和期望．
附：若随机变量，则，，．
三年考情分析
2025考向预测
2022年，第4题，考察频率分布直方图；
第13题条件概率
2023年，第7题，考察正负相关性；
第13题独立事件的概率公式
2024年，第3题，考察根据散点图判断是否线性相关；第13题古典概型和条件概率
概率统计专题相关的知识点错综复杂又环环相扣，在天津高考中近三年以图表信息、古典概型、条件概率，回归分析，独立性检验、样本估计总体等为主要考查内容，主要以选填形式出现。
（1）分层随机抽样的步骤
①根据己经掌握的信息，将总体分成互不相交的层；
②根据总体中的个体数和样本量计算抽样比；
③确定第层应该抽取的个体数目（为第层所包含的个体数），使得各之和为；
④在各个层中，按步骤③中确定的数目在各层中随机抽取个体，合在一起得到容量为的样本.
分层抽样的均值与方差
产品
产品
产品
普通装

180
400
精品装
300
420
600
1、计算一组个数据的第百分位数的步骤：
第1步,按从小到大排列原始数据.
第2步,计算.
第3步,若不是整数,而大于的比邻整数为,则第百分位数为第项数据;若是整数,则第百分位数为第项与第项数据的平均数.
2、在频率分布直方图中，众数，中位数，平均数的估计值
(1)最高的小矩形底边中点的横坐标即是众数;
(2)中位数左边和右边的所有小矩形的面积和是相等的;
(3)平均数是频率分布直方图的“重心”,等于频率分布直方图中每个小矩形的面积乘小矩形底边中点的横坐标之和.
事件的相互独立性
（1）事件与事件相互独立：对任意的两个事件与,如果成立，则称事件与事件相互独立，简称为独立.
（2）性质：若事件与事件相互独立，则与,与,与也都相互独立，, .
条件概率：一般地，设，为两个随机事件，且，我们称为在事件发生的条件下，事件发生的条件概率，简称条件概率．
全概率公式：
贝叶斯公式：
将称为关于的线性回归方程，也称经验回归函数或经验回归公式，其图形称为经验回归直线。这种求经验回归方程的方法叫做最小二乘法，求得的，叫做，的最小二乘估计,其中称为回归系数，它实际上也就是经验回归直线的斜率，为截距.
其中
年份
2018年
2019年
2020年
2021年
2022年
年份代码
1
2
3
4
5

2
2.4
3
3.6
4
6
8
10
12
7
4
3
时间
1
2
3
4
5
交易量（万套）
0.8
1.0
1.2
1.5
广告费用x（万元）
1
2
4
5
销售额y（万元）
10
26
35
49
独立性检验公式：
其中（注意使用公式时分子的平方不要忽略了）
药物
疾病B
合计
未患病
患病
未服用
7
服用
8
19
合计
0.100
0.050
0.025
2.706
3.841
5.024
认为作业多
认为作业不多
总计
喜欢玩电脑游戏
不喜欢玩电脑游戏
总计
不喜欢垃圾分类
喜欢垃圾分类
合计
男
女
合计
满意
不满意
合计
上班族
非上班族
合计
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
一般地，在重伯努利试验中，设每次试验中事件发生的概率为()，用表示事件发生的次数，则的分布列为，.
如果随机变量的分布列具有上式的形式，则称随机变量服从二项分布，记作．
一般地，假设一批产品共有件，其中有件次品，从件产品中随机抽取件(不放回)，用表示抽取的件产品中的次品数，则的分布列为，.
其中，，，，．
如果随机变量的分布列具有上式的形式，那么称随机变量服从超几何分布．
若随机变量的概率密度函数为，(,其中，为参数)，称随机变量服从正态分布，记为.
平均作业时长（单位：小时）
学业成绩优秀：
学业成绩不优秀：
出行方式
地铁
公交车
出租车
自驾
骑行
步行
频数
54
27
38
42
18
21