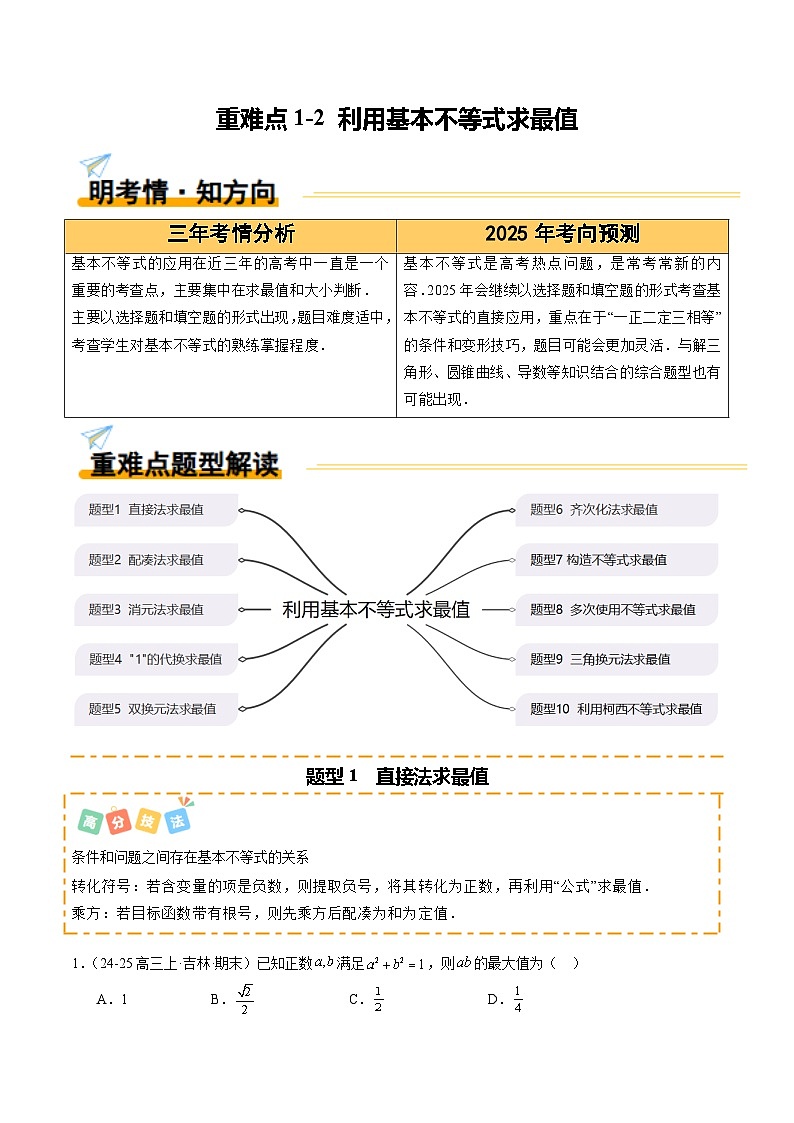
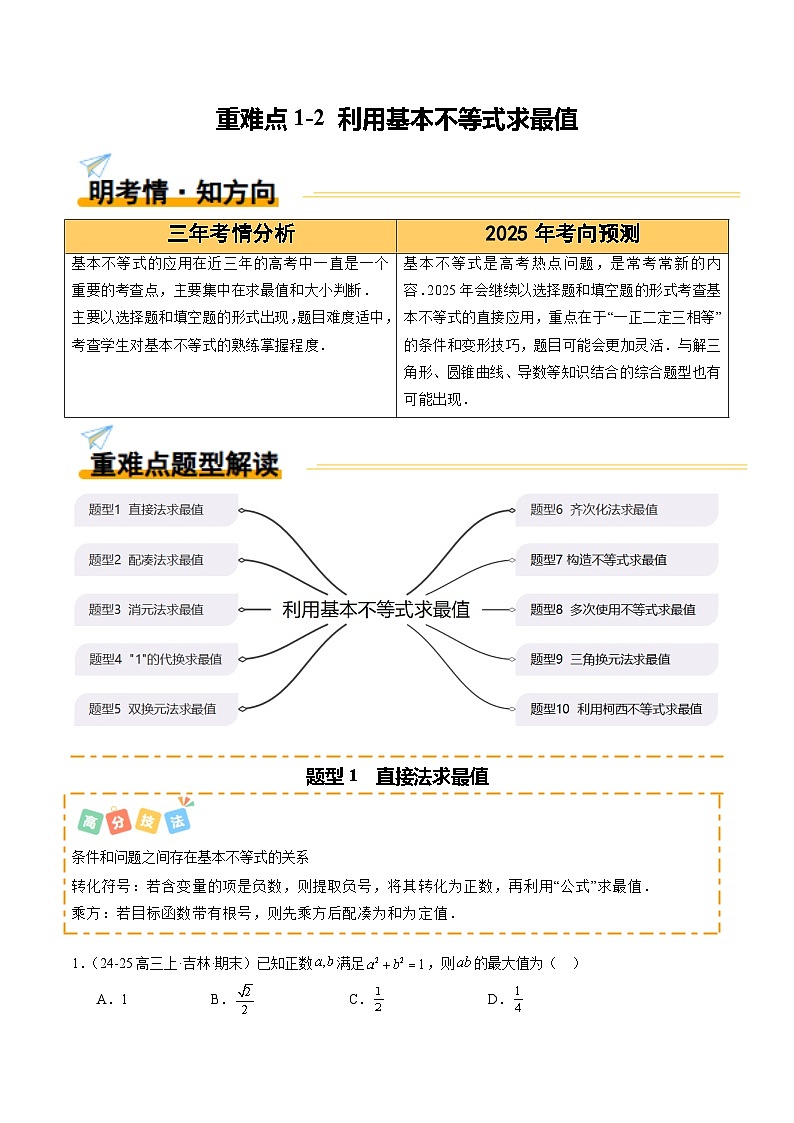
重难点1-2 利用基本不等式求最值（10题型 高分技法 限时提升练）-2025年高考数学 热点 重点 难点 专练（新高考通用）

这是一份重难点1-2 利用基本不等式求最值（10题型 高分技法 限时提升练）-2025年高考数学 热点 重点 难点 专练（新高考通用），文件包含重难点1-2利用基本不等式求最值10题型高分技法限时提升练-2025年高考数学热点重点难点专练新高考通用原卷版docx、重难点1-2利用基本不等式求最值10题型高分技法限时提升练-2025年高考数学热点重点难点专练新高考通用解析版docx等2份试卷配套教学资源，其中试卷共37页， 欢迎下载使用。

题型1 直接法求最值
1．（24-25高三上·吉林·期末）已知正数满足，则的最大值为（ ）
A．1B．C．D．
2．（24-25高三上·河南驻马店·月考）已知，且，则的最小值为（ ）
A．2B．4C．6D．8
3．（24-25高三上·吉林松原·期末）已知正数满足，则的最小值为 .
4．已知正数，满足，则的最小值是 .
题型2 配凑法求最值
1．（24-25高三上·贵州·期中）的最小值为 ．
2．（24-25高三上·北京·月考）的值可以为（ ）
A．−8B．C．8D．9
3．（24-25高三上·天津河西·期中）已知，，且，则的最大值为（ ）
A．6B．C．D．
4．（24-25高三上·甘肃白银·期中）已知，则的最小值为（ ）
A．2B．4C．6D．8
题型3 消元法求最值
1．（24-25高三上·新疆·月考）已知，则的最大值为 ．
2．（24-25高三上·重庆·月考）已知，且，则的最小值为（ ）
A．B．C．D．
3．（24-25高三上·四川成都·期中）已知，，则的最小值是（ ）
A．B．C．D．17
4．（24-25高三上·海南·月考）已知，，且，则的最小值为（ ）
A．3B．5C．7D．8
题型4 “1”的代换求最值
1．（24-25高三上·安徽·月考）已知，，，则的最小值为（ ）
A．4B．2C．D．
2．（24-25高三上·陕西西安·期末）已知正数满足，则的最小值为（ ）
A．B．C．5D．9
3．（24-25高三上·河北唐山·期末）已知，则的最小值为 ．
4．（24-25高三上·山东济宁·期末）若，且，则的最小值为（ ）
A．B．C．3D．4
题型5 双换元法求最值
1．已知正实数满足且，则的最小值为
2．（24-25高一上·重庆·期中）若正实数，满足，则的最小值是 .
3．（24-25高三上·江苏·月考）对于任意的，，恒成立，则的最大值为（ ）
A．B．C．D．
4．（24-25高三上·江西南昌·月考）设实数满足，则的最小值为（ ）
A．B．C．D．1
题型6 齐次化法求最值
1．（24-25高三上·河南·月考）已知，则的最小值为 .
2．（24-25高三上·江苏苏州·期中）已知实数，则的最小值为（ ）
A．12B．9C．6D．3
3．（24-25高三上·甘肃白银·月考）已知x，y为正实数，则的最小值为 ．
4．（23-24高三下·湖北·一模）已知正实数满足，则的最大值为 .
题型7 构造不等式求最值
1．（24-25高三上·广东广州·月考）若，且，则的取值范围是（ ）
A．B．C．D．
2．（24-25高三上·浙江杭州·期末）已知，则的最小值为（ ）
A．B．9C．D．10
3．（23-24高三下·湖北·一模）已知实数满足，则最大值为（ ）
A．2B．3C．D．
4．（24-25高三上·广东湛江·月考）已知正数 满足 ，则的取值范围为（ ）
A．B．C．D．
题型8 多次使用不等式求最值
1．（24-25高三上·湖南长沙·月考）已知，，，且恒成立，则的取值范围是 .
2．（24-25高三上·福建宁德·月考）已知正数a，b，c满足，，则的最小值为 .
3．（23-24高三上·江苏南京·月考）设正实数满足，且，则的最小值为 .
4．（24-25高一上·辽宁沈阳·月考），，，满足，则的最小值为（ ）
A．B．C．D．
题型9 三角换元法求最值
1．（24-25高三上·江苏盐城·期中）若实数x，y满足，则的最小值为（ ）
A．1B．C．D．
2．（24-25高三上·甘肃白银·期末）已知，则的最大值为（ ）
A．B．C．D．
3．（24-25高三上·辽宁·开学考试）已知均为正数，，则的最大值为 .
4．（24-25高三上·安徽合肥·月考）已知正数x，y满足，则的最小值为（ ）
A．1B．2C．3D．4
题型10 利用柯西不等式求最值
1．（24-25高三上·北京朝阳·模拟预测）函数的最大值为（ ）
A．1B．C．2D．
2．（24-25高三上·陕西西安·月考）已知，，则的最小值为 ．
3．（24-25高一上·陕西西安·月考）存在正数使得不等式成立，则的最大值是 .
4．（24-25高三上·广西钦州·月考）（多选）已知，，且不等式恒成立，则的取值可能是（ ）
A．B．C．D．
（建议用时：60分钟）
一、单选题
1．（24-25高三上·重庆·期末）已知，则的最小值为（ ）
A．B．C．D．100
2．（24-25高三上·四川广安·月考）已知正实数x，y满足，则的最小值为（ ）
A．9B．10C．11D．12
3．（24-25高三上·广东中山·月考）若正实数，满足，则的最小值为（ ）
A．9B．6C．3D．2
4．（24-25高三上·湖北黄冈·月考）若，且，则的最小值为（ ）
A．20B．12C．16D．25
5．（24-25高三上·江西上饶·月考）已知实数满足，则的最小值为（ ）
A．9B．18C．27D．36
6．（24-25高三上·江苏·月考）已知，，，则的最小值为（ ）
A．4B．5C．6D．
7．（23-24高三下·山东淄博·二模）记表示中最大的数．已知均为正实数，则的最小值为（ ）
A．B．1C．2D．4
8．（24-25高三上·天津河东·期末）已知且，则的最小值为（ ）
A．B．C．D．
二、多选题
9．（24-25高三上·江苏镇江·月考）已知，，且，则（ ）
A．的最小值为B．的最小值为9
C．的最小值为D．的最小值为
10．（24-25高三上·山西·月考）已知为正实数，且，则（ ）
A．的最小值为8B．的最小值为
C．的最大值为D．的最小值为
11．（24-25高三上·重庆·模拟预测）若 ，则下列说法正确的是（ ）
A．B．
C．D．
12．（24-25高三上·江苏泰州·月考）已知均为正实数，则下列说法正确的是（ ）
A．的最大值为
B．若，则的最大值为8
C．若，则的最小值为
D．若，则的最小值为
三、填空题
13．（24-25高三上·福建·月考）已知，，则的最小值为 .
14．若x，y满足，则的最大值为
15．（24-25高三上·天津河西·月考）已知，，，则的最小值为 .
16．（24-25高三上·山东泰安·期中）已知，，，则的最小值为 .三年考情分析
2025年考向预测
基本不等式的应用在近三年的高考中一直是一个重要的考查点，主要集中在求最值和大小判断．
主要以选择题和填空题的形式出现，题目难度适中，考查学生对基本不等式的熟练掌握程度．
基本不等式是高考热点问题，是常考常新的内容．2025年会继续以选择题和填空题的形式考查基本不等式的直接应用，重点在于“一正二定三相等”的条件和变形技巧，题目可能会更加灵活．与解三角形、圆锥曲线、导数等知识结合的综合题型也有可能出现．
条件和问题之间存在基本不等式的关系
转化符号：若含变量的项是负数，则提取负号，将其转化为正数，再利用“公式”求最值．
乘方：若目标函数带有根号，则先乘方后配凑为和为定值．
将目标函数恒等变形或适当放缩，配凑出两个式子的和或积为定值.
配凑法的实质在于代数式的灵活变形，配系数、凑常数是关键。
利用配凑法求解最值应注意以下几个方面的问题：
（1）配凑的技巧，以整式为基础，注意利用系数的变化以及等式中常数的调整，做到等价变形；
（2）代数式的变形以配凑出和或积的定值为目标；
（3）拆项、添项应注意检验利用基本不等式的前提．
根据条件与所求均含有两个变量，从简化问题的角度来思考，消去一个变量，转化为只含有一个变量的函数，然后转化为函数的最值求解．有时会出现多元的问题，解决方法是消元后利用基本不等式求解．注意所保留变量的取值范围．
1、若已知条件中的“１”（常量可化为“１”）与目标函数之间具有某种关系（尤其是整式与分式相乘模型），则实施“１”代换，配凑和或积为常数.
模型1：已知正数满足，求的最小值。
模型2：已知正数满足求的最小值。
2、常数代换法适用于求解条件最值问题．应用此种方法求解最值的基本步骤为：
（1）根据已知条件或其变形确定定值(常数)；
（2）把确定的定值(常数)变形为1；
（3）把“1”的表达式与所求最值的表达式相乘或相除，进而构造和或积的形式；
（4）利用基本不等式求解最值．
双换元法是“1”的代换更复杂情况的应用，常用于分母为多项式的情况．
具体操作如下：如分母为与，分子为，
设
∴，解得：
另外，当形式比较复杂时，也可以考虑使用换元法进行化简．
适用于能构造成分式，且分式上下为齐次式的题型，构造齐次式后则可进行下面的操作
再进行换元则题目变成分式类型，按照单变量分式类型计算即可．
当条件式中给出了"和"与"积"之间的关系时，可以考虑借助基本不等式进行放缩，由条件式构建得到关于"和"或"积"的不等式，解此不等式即可求得"和"或"积"的最值．
同一式子中若使用多次基本不等式，需满足以下两个条件：（1）不等号的方向已知；（2）取等条件一致．
适用于双变量不等式能构造平方和形式的题型．利用进行换元．
例如
适用于：已知的值，求的取值范围，或者已知的值，求的最值或求的最值．
（1）二维柯西不等式：设均为实数，有，当且仅当时等号成立．
（2）维柯西不等式：，其中字母值域均为，当且仅当时等号成立．