初中数学冀教版（2024）七年级下册（2024）第十章 三角形10.2 三角形的内角和外角示范课ppt课件

这是一份初中数学冀教版（2024）七年级下册（2024）第十章 三角形10.2 三角形的内角和外角示范课ppt课件，共24页。PPT课件主要包含了∠DAC，谈一谈，锐角三角形，直角三角形，钝角三角形，在△ABC中，又∵∠B∠BAD，解是钝角三角形，已知一个外角是55°等内容，欢迎下载使用。
1.了解三角形外角的概念.2.掌握三角形外角的性质.
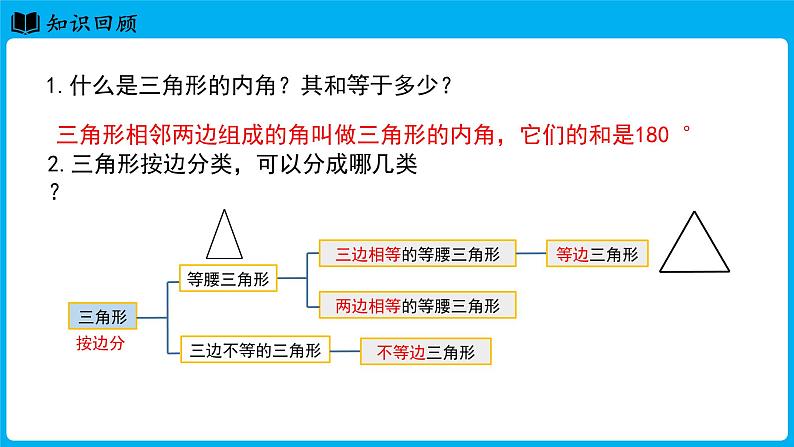
1.什么是三角形的内角？其和等于多少？
三角形相邻两边组成的角叫做三角形的内角，它们的和是180 °
2.三角形按边分类，可以分成哪几类？
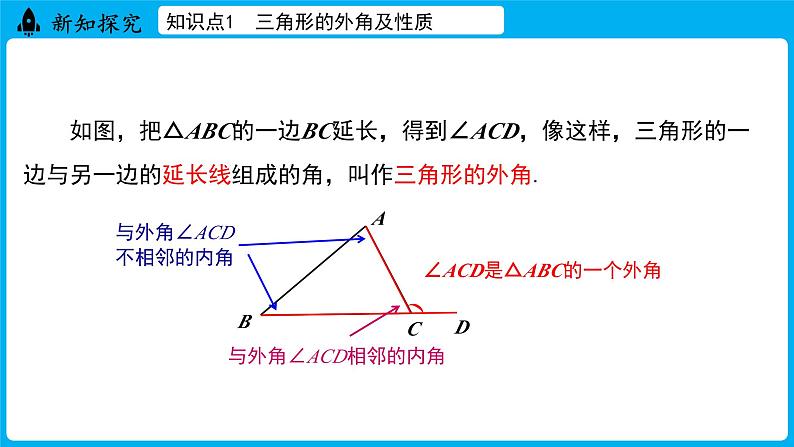
如图，把△ABC的一边BC延长，得到∠ACD，像这样，三角形的一边与另一边的延长线组成的角，叫作三角形的外角.
∠ACD是△ABC的一个外角
与外角∠ACD不相邻的内角
与外角∠ACD相邻的内角
知识点1 三角形的外角及性质
问题1：△ABC如图所示，请画出△ABC的所有外角，指出来有哪几个.
有6个，它们是∠1， ∠2， ∠3， ∠4， ∠5， ∠6.
问题2：△ABC的6个外角有什么关系?
∠1和∠4, 是对顶角，相等；∠2和∠5, 是对顶角，相等；∠3和∠6, 是对顶角，相等.
问题3：在图中，外角∠ACD与它不相邻的内角∠A，∠B之间有什么大小关系？
解：∵∠ACD+∠ACB = 180°，(补角的定义） ∠A +∠B +∠ACB = 180°，(三角形的内角和定理）
∴∠ACD-∠A-∠B = 0.
∴∠ACD =∠A +∠B.
∵∠A＞0，∠B＞0，
∴∠ACD＞∠A，∠ACD＞∠B.
三角形的外角的性质三角形的一个外角等于与它不相邻的两个内角的和.三角形的一个外角大于与它不相邻的任意一个内角.
练一练 1.如图，口答：（1）∠1 = + ；（2）∠2 = + ．
练一练 2.如图，说出图形中∠1 的度数．
例1 如图，∠BCD=92°，∠A=27°，∠BED=44°，求： (1) ∠B的度数；(2) ∠BFD的度数；
解：(1) 在△ABC中，∵ ∠BCD=∠A+∠B(三角形的一个外角等于与它不相邻的两个内角的和),∠BCD=92°，∠A=27°，(已知)
∴∠B=∠BCD-∠A=92°-27°=65°；
(2) 在△BEF中，∵ ∠BFD=∠B+∠BED(三角形的一个外角等于与它不相邻的两个内角的和),∠BED=44°，∠B=65°，(已知)
∴∠BFD=44°+65°=109°.
例2 (一题多解）如图，计算∠BDC.
解：（解法一）连接AD并延长于点E.在△ABD中，∠1+∠ABD=∠3，在△ACD中，∠2+∠ACD=∠4.因为∠BDC=∠3+∠4，∠BAC=∠1+∠2，所以∠BDC=∠BAC+∠ABD+∠ACD =51° +20°+30°=101°.
（解法二）延长BD交AC于点E.在△ABE中，∠1=∠ABE+∠BAE，在△ECD中，∠BDC=∠1+∠ECD.所以∠BDC=∠BAC+∠ABD+∠ACD =51° +20°+30°=101°.
练一练 如图，∠BAE，∠CBF，∠ACD 是△ABC 的三个外角，它们的和是多少？
解法一：∵　∠BAE =∠2 +∠3， ∠CBF =∠1 +∠3， ∠ACD =∠1 +∠2，∴　∠BAE +∠CBF +∠ACD= （∠2 +∠3）+（∠1 +∠3）+ （∠1 +∠2）
= 2（∠1 +∠2 +∠3）．∵　∠1 +∠2 +∠3 =180°，∴　∠BAE +∠CBF +∠ACD = 2×180°=360°.
由∠1 + ∠2 + ∠3 =180°，得∠BAE + ∠CBF + ∠ACD = 540°- 180° =360°.
解法二：由∠1 +∠BAE =180°，∠2 +∠CBF =180°，∠3 +∠ACD =180°，得∠1 +∠2 +∠3 + ∠BAE+∠CBF +∠ACD = 540°．
归纳：三角形的外角和360°.
1.一个三角形的内角最多有几个直角，最多有几个钝角？2.一个三角形能不能三个内角都是锐角？
知识点2 三角形按角分类
问题4：按照三角形内角的大小，三角形可以分为哪几类？
三个内角都是锐角的三角形
有一个内角是直角的三角形
有一个内角是钝角的三角形
请你试着以角为标准对三角形进行分类
练一练：下列说法正确的是( )A.所有的等腰三角形都是锐角三角形B.等边三角形属于等腰三角形C.不存在既是钝角三角形又是等腰三角形的三角形D.一个三角形中有两个锐角，则一定是锐角三角形
1.判断下列命题的对错.（1）三角形的外角和是指三角形的所有外角的和. （ ）（2）三角形的外角和等于它的内角和的2倍. （ ）（3）三角形的一个外角等于两个内角的和. （ ）（4）三角形的一个外角等于与它不相邻的两个内角的和.（ ）（5）三角形的一个外角大于任何一个内角. （ ）（6）三角形的一个内角小于任何一个与它不相邻的外角.（ ）
2.如图，AB//CD，∠A＝37°, ∠C＝63°，那么∠F等于_____.
3.如图，已知l1∥l2,∠A=40°,∠1=60°,则∠2的度数为_______.
4. 如图，D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°，∠BAC=70°，求：（1）∠B 的度数； （2）∠C的度数.
∠B+∠BAC+∠C=180°，
∠C=180º-40º-70º=70°.
解：∵∠ADC是△ABD的外角.
∴∠ADC=∠B+∠BAD=80°.
5.已知某三角形的一个外角是55°，这个三角形是锐角三角形、直角三角形，还是钝角三角形？
∴和这个外角相邻的内角是125°.
∴这个三角形是钝角三角形.