第5章 图形的轴对称 章末小结（课件）2024—2025学年北师大版（2024）数学七年级下册

这是一份第5章 图形的轴对称 章末小结（课件）2024—2025学年北师大版（2024）数学七年级下册，共35页。
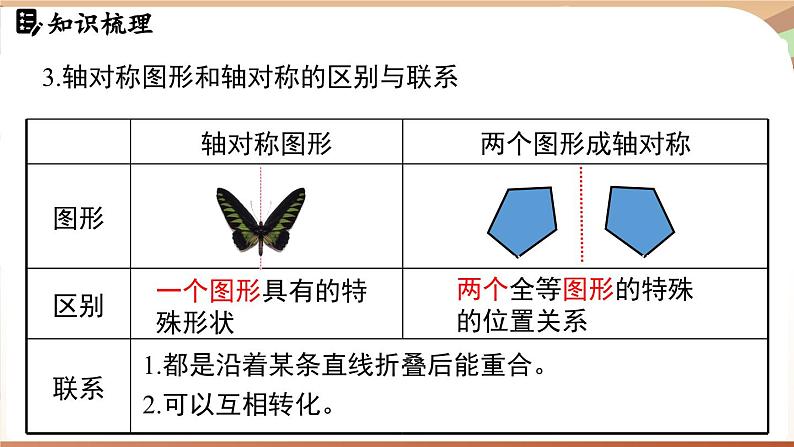
第五章 图形的轴对称章末小结轴对称图形生活中的轴对称现象轴对称的性质简单的轴对称图形等腰三角形线段角两个图形成轴对称画图尺规作图一、轴对称及其性质(一)轴对称1.轴对称图形如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，那么这个图形叫作轴对称图形。这条直线就是它的对称轴。2.轴对称如果两个平面图形沿一条直线对折后能够完全重合，那么称这两个图形成轴对称这条直线叫作这两个图形的对称轴。3.轴对称图形和轴对称的区别与联系 一个图形具有的特殊形状两个全等图形的特殊的位置关系1.都是沿着某条直线折叠后能重合。2.可以互相转化。(二)轴对称的性质:1.轴对称的基本性质:在轴对称图形或两个成轴对称的图形中，对应点所连的线段被对称轴垂直平分，对应线段相等，对应角相等。2.性质的应用：利用对应角相等求角度；利用对应线段相等求线段，求面积，求周长；作图。(三)画图补全轴对称图形，或画成轴对称的另一个图形。画图依据：对称两点到对称轴的距离相等解:，图(1)(3)(5)(6)是轴对称图形；图(2)(4)(7)不是轴对称图形。1. 图中的图形是不是轴对称图形?若是，请画出其对称轴，并说出对称轴的条数。1. 图中的图形是不是轴对称图形?若是，请画出其对称轴，并说出对称轴的条数。2.如图所示，点P关于直线OA，OB的对称点分别为点C，D，CP，PD分别交OA，OB于点E，F，连接CD，交OA于点M，交OB于点N，连接PM，PN。(1)若△PMN的周长为8，求CD的长。(2)若∠AOB=45°，求∠MPN的度数。(1)解:因为点P关于直线OA，OB的对称点分别为点C，D，所以PM=CM，PN=DN，因为△PMN的周长为8，所以PM+PN+MN=8，所以CD=CM+DN+MN=PM+PN+MN=8，即CD=8。2.如图所示，点P关于直线OA，OB的对称点分别为点C，D，CP，PD分别交OA，OB于点E，F，连接CD，交OA于点M，交OB于点N，连接PM，PN。(1)若△PMN的周长为8，求CD的长。(2)若∠AOB=45°，求∠MPN的度数。(2)解:因为点P关于直线OA，OB的对称点分别为点C，D，所以PM=CM，PN=DN，所以∠C=∠CPM，∠D=∠DPN，因为∠AOB=45°，所以∠CPD=360°-90°-90°-45°=135°，所以∠C+∠D=180°-∠CPD=45°，所以∠CPM+∠DPN=45°，所以∠MPN=∠CPD-(∠CPM+∠DPN)=135°-45°=90°。分析:挖掘出折叠前后相等的线段或角，可实现线段或角的转换，这是求解折叠问题的关键。3.如图，在Rt△ABC中，∠ACB=90°，AB=10，AC=6，BC=8，点D在AB边上，将△ACD沿直线CD折叠，使点A恰好落在BC边上的点E处。(1)求△BDE的周长。(2)若∠B=37°，求∠EDB的度数。解:(1)由折叠可知AC=CE，AD=DE。因为AC=6，所以CE=6，因为BC=8，所以BE=BC-CE=2，所以△BDE的周长=DE+BD+EB =AD+BD+EB=AB+EB。 3.如图，在Rt△ABC中，∠ACB=90°，AB=10，AC=6，BC=8，点D在AB边上，将△ACD沿直线CD折叠，使点A恰好落在BC边上的点E处。(2)若∠B=37°，求∠EDB的度数。(2)由折叠可知∠A=∠CED，因为∠B=37°，所以∠A=∠CED=180°-∠ACB-∠A =180°-90°-37°=53°，所以∠ADE=360°-∠ACB-∠A-∠CED =360°-90°-53°-53°=164°，所以∠EDB=180°-∠ADE=180°-164°=16°。分析:确定已知图形的关键点；作关键点的对称点；连接对称点得所求图形。4.如图所示，以虚线为对称轴，画出图形的另一半。解:如图所示:(1)延长AO到点A′，使A′O=AO；(2)延长BP到点B′，使B′P=BP，在B′P上截取 D′P=DP；(3)延长CQ到点C′，使C′Q=CQ；(4)分别作点E，F，H，G关于虚线的对称点E′，F′，H′ ，G′；(5)连接A′，B′，D′，C′，再依次连接E′F′，F′H′，H′G′，G′E′，即画出了图形的另一半。二、简单的轴对称图形(一)等腰三角形的性质1.等腰三角形是轴对称图形。2.等腰三角形的顶角平分线、底边上的高和底边上的中线互相重合(简称“三线合一”)。3.等腰三角形的两个底角相等。(二)等边三角形的性质1.等边三角形是轴对称图形，共有三条对称轴。2.等边三角形每个角的平分线和这个角的对边上的中线、高线重合(简称“三线合一”)，它们所在的直线都是等边三角形的对称轴。3.等边三角形的各角都相等，都等于60°。(三)线段的垂直平分线1.定义：垂直于一条线段，并且平分这条线段的直线，叫作这条线段的垂直平分线。2.线段垂直平分线的性质：线段垂直平分线上的点到这条线段两个端点的距离相等。3.线段的对称轴：这条线段的垂直平分线。(四)角平分线1.角平分线的性质:角的平分线上的点到角的两边的距离相等。2.定理的作用:证明线段相等。5.如图，△AOD关于直线l进行轴对称变换后得到△BOC，下列说法不正确的是（ ）A． ∠DAO=∠CBO，∠ADO=∠BCOB． 直线∠垂直平分AB、CDC． AO⊥OB，DO⊥OCD． AD=BC，OD=OCC 6.如图所示，已知在等腰三角形ABC中，点D，E在BC上，AB=AC，AD=AE.试说明:BD=CE。分析：作AH⊥BC；需说明BH=CH，DH=EH。方法二 如图所示.过点A作AH⊥BC于点H。因为AB=AC，AH⊥BC，所以BH=CH。同理可得，DH=EH，所以BH-DH=CH-EH，即BD=CE。6.如图所示，已知在等腰三角形ABC中，点D，E在BC上，AB=AC，AD=AE.试说明:BD=CE。分析:7.如图，线段AB，BC的垂直平分线l1，l2相交于点O，连接AO，CO，若∠1=39°，则∠AOC= 。l1，l2分别为线段AB，BC的垂直平分线(可设D，E为垂足)连接OB△AOB是等腰三角形△BOC是等腰三角形解析:如图，连接OB，设l1交AB于点D，l2交BC于点E。因为线段AB，BC的垂直平分线l1，l2相交于点O，所以OA=OB=OC。因为l1⊥AB， l2⊥BC，所以∠AOD=∠BOD，∠BOE=∠COE，所以∠AOD+∠COE=∠BOD+∠BOE=∠DOE。因为∠DOE+∠1=180°，∠1=39°，所以∠DOE=141°，所以∠AOC=360°-∠DOE-(∠AOD+∠COE)=360°-2∠DOE=360°-2×141°=78°。7.如图，线段AB，BC的垂直平分线l1，l2相交于点O，连接AO，CO，若∠1=39°，则∠AOC= 。78°8.如图，AD//BC，∠ABC的平分线 BP与∠BAD的平分线AP相交于点P，作PE⊥AB于点E，若PE=2.5，则平行线AD与BC之间的距离为( )A.3 B.4 C.5 D.6解析:如图，过点P作GH⊥AD交AD于点G，交BC于点H，因为AD//BC，所以GH⊥BC，因为AP平分∠BAD，PE⊥AB，PG⊥AD，所以PG=PE=2.5，同理可得PH=PE=2.5，所以GH=PG+PH=5，即平行线AD与BC之间的距离为5。8.如图，AD//BC，∠ABC的平分线 BP与∠BAD的平分线AP相交于点P，作PE⊥AB于点E，若PE=2.5，则平行线AD与BC之间的距离为( )A.3 B.4 C.5 D.6C9.如图，校园内有两条路 OA，OB，在交叉口附近有两块宣传牌C，D，学校准备在这里安装一盏路灯，要求灯柱的位置P到两块宣传牌的距离相等，并且到两条路的距离也相等，请你帮忙找到灯柱的位置P，并说明理由。 AC DO B思路引导：到两块宣传牌的距离相等到两条路的距离相等两条线的交点为点P的位置点P在OA，OB央角的平分线上点P在C，D所连线段的垂直平分线上 AC DO B AC DO B解: 如图，连接CD。分别作线段CD的垂直平分线EF和∠AOB的平分线OG，EF与OG相交于点P，则点P就是所要确定的灯柱的位置。P