高中物理人教版 (2019)必修 第二册第八章 机械能守恒定律1 功与功率教课内容ppt课件

这是一份高中物理人教版 (2019)必修 第二册第八章 机械能守恒定律1 功与功率教课内容ppt课件，文件包含本章整合pptx、第八章测评docx等2份课件配套教学资源，其中PPT共21页， 欢迎下载使用。
突破点一　求变力做功的几种方法
1.用转换对象法求变力做功W=Flcs θ是恒力做功的计算公式,有些问题需要求解变力做的功,我们可以利用转换对象法巧妙地将变力做功转化为恒力做功,从而使问题迎刃而解。2.用微元法求变力做功当力的大小不变、方向变化且位移的方向也同步变化时,可用微元法求解,此时力做的功等于力和路程的乘积。由于变力F保持与速度在同一直线上,也可把往复运动或曲线运动的路线拉直考虑。
3.用动能定理法求变力做功有些题目不能直接应用功的定义式来计算,我们可以借助动能定理来分析变力做的功。4.用图像法求变力做功在F-x图像中,图线和横轴所围成的面积表示力做的功。有些看似复杂的变力做功问题,用常规方法无从下手时,可以尝试通过图像变换解题。5.用公式W=Pt求变力做功如果变力的功率恒定、时间已知,可以用 W=Pt求解变力做的功。6.求平均力将变力转化为恒力如果力是随位移均匀变化的,可用求平均力的方法将变力转化为恒力。
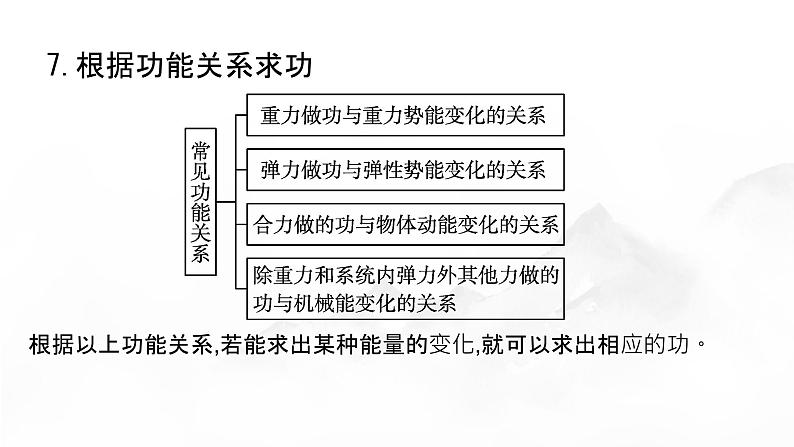
根据以上功能关系,若能求出某种能量的变化,就可以求出相应的功。
【例1】 (多选)如图所示,一个质量为m的圆环套在一根固定的水平直杆上,杆足够长,环与杆的动摩擦因数为μ,现给环一个向右的初速度v0,如果在运动过程中还受到一个方向始终竖直向上的力F,F=kv(k为常数,v为环的速率),则环在整个运动过程中克服摩擦力所做的功可能为(　　)
解析 依题意,分以下三种情形:情景一,给环一个向右的初速度v0,如果重力恰好等于F,则物体做匀速直线运动,摩擦力为0,不做功;情景二,如果环受摩擦力则做减速运动,若开始时环的重力大于F,支持力方向向上速度最终减
1.(多选)为早日实现无人驾驶,某公司对某款汽车性能进行了一项测试,让质量为m的汽车以恒定的牵引力从静止启动加速运动,经过时间t0,速度刚好达到v1,之后汽车以恒定功率P运行至最大速度vm,汽车速度由0到vm所用时间为t,已知vm>2v1,设汽车在运动过程中所受阻力保持不变,下列说法正确的是(　　)
突破点二　动力学方法和能量观点的综合运用
涉及动力学方法和能量观点的综合题,应根据题目要求灵活选用公式和规律。(1)涉及力和运动的瞬时性分析或恒力作用下物体做匀变速直线运动的问题时,可用牛顿运动定律。(2)用动能定理求解物体受恒力作用下的问题比用牛顿运动定律求解过程要简单,变力作用下的问题只能用能量观点。(3)涉及动能与势能的相互转化,单个物体或系统机械能守恒问题时,通常选用机械能守恒定律。
【例2】 如图所示,竖直平面内由倾角α=60°的斜面轨道AB、半径均为R的半圆形细圆管轨道BCDE和 圆周细圆管轨道EFG构成一游戏装置固定于地面,B、E两处轨道平滑连接,轨道所在平面与竖直墙面垂直。轨道出口处G和圆心O2的连线,以及O2、E、O1和B等四点连成的直线与水平线间的夹角均为θ=30°,G点与竖直墙面的距离d= R。现将质量为m的小球从斜面的某高度h处静止释放。不计小球大小和所受阻力。
(1)若小球经过圆管内与圆心O1点等高的D点时对轨道的压力等于mg,求小球经过D点时的速度大小;(2)若小球释放后能从G点冲出,并垂直打到竖直墙壁,求:①小球冲出G点时的速度大小;②小球第一次运动到圆管最低点C时,小球对轨道的压力大小;(3)若小球释放后能从G点冲出,并打到竖直墙壁与G点等高的位置,求释放点的高度h。
(2)①小球垂直打到竖直墙壁,从G点到竖直墙壁的运动为平抛运动的逆过程。有vxt=d,vy=gt其中vx=vGsin θ,vy=vGcs θ
(3)小球从G点冲出到竖直墙壁与G点等高位置的运动过程为斜抛运动,根
2.(多选)(2023河南南阳高一期末)如图所示,绷紧的传送带与水平面的夹角为θ,传送带在电动机的带动下,始终保持v0的速率顺时针运行。现把一物块(可看为质点)轻放在传送带底端,物块被传送到最高点(在运动至最高点前已与传送带达到共速)。已知物块与传送带间动摩擦因数为μ,且μ>tan θ,t为运动时间,x为物块沿斜面运动的距离。以最低点所在水平面为参考平面,设物块在传送带上时的速度为v,重力势能为Ep,机械能为E,物块和传送带摩擦产生的热量为Q,则下列关系图像中与实际情况相符的是(　　)
解析 物块刚放到传送带上时,相对传送带向下运动,则由牛顿第二定律得μmgcs θ-mgsin θ=ma,可得加速度a=μgcs θ-gsin θ,物块的速度为v1=at=(μgcs θ-gsin θ)t,物块做初速度为零的匀加速运动,当物块速度等于传送带速度后,物块相对传送带静止,随传送带做匀速运动,故A正确;在物