初中数学湘教版（2024）七年级下册（2024）4.4 平行线的判定教课课件ppt

这是一份初中数学湘教版（2024）七年级下册（2024）4.4 平行线的判定教课课件ppt，文件包含442用内错角同旁内角判定平行线pptx、442用内错角同旁内角判定平行线doc等2份课件配套教学资源，其中PPT共19页， 欢迎下载使用。
如图所示，直线AB与CD被直线EF所截，
因为∠___=∠___，
理由:__________________________.
同位角相等，两直线平行
两条直线被第三条直线所截，由同位角相等可以判定两条直线平行，那么内错角相等可以判定两条直线平行吗？同旁内角互补呢？
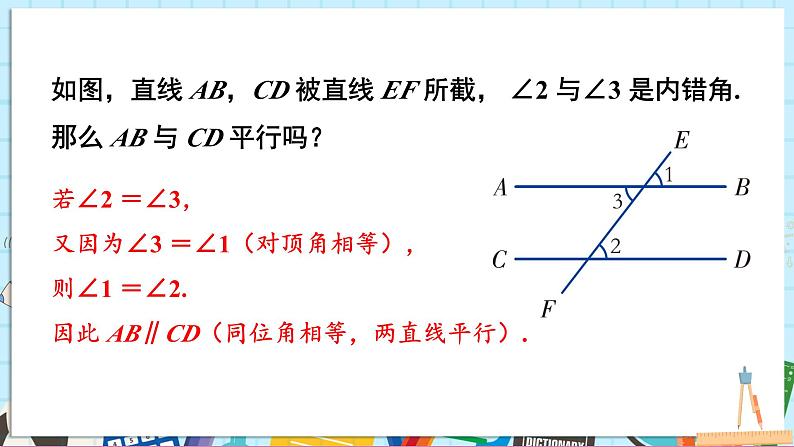
如图，直线 AB，CD 被直线 EF 所截， ∠2 与∠3 是内错角. 那么 AB 与 CD 平行吗？
若∠2 ＝∠3，又因为∠3 ＝∠1（对顶角相等），则∠1 ＝∠2.因此 AB∥CD（同位角相等，两直线平行）.
简单说成：内错角相等，两直线平行.
判定方法2 两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行.
如图，直线 AB，CD 被直线 EF 所截， ∠1 与∠2是同旁内角 .那么 AB 与 CD 平行吗？
若∠1 +∠2 = 180°，又因为∠2 +∠3 = 180°，则 ∠3 =∠1.因此 AB∥CD （同位角相等，两直线平行） .
简单说成：同旁内角互补，两直线平行.
判定方法3 两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行.
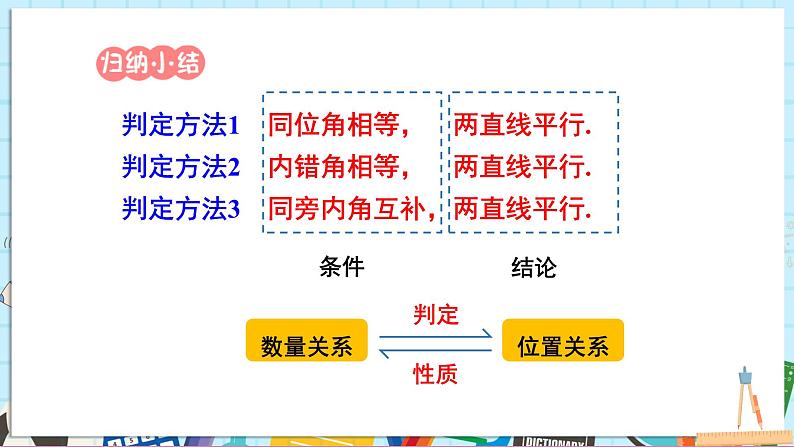
判定方法1 同位角相等， 两直线平行.
判定方法2 内错角相等， 两直线平行.
判定方法3 同旁内角互补，两直线平行.
解: 因为 AB∥DC，所以∠1 ＝∠2（两直线平行，内错角相等）．又因为∠BAD ＝∠BCD ，所以∠BAD －∠1 ＝∠BCD －∠2．即∠3 ＝∠4．所以 AD∥BC（内错角相等，两直线平行）．
解: 因为 AD∥BC，所以∠1 +∠3= 180°(两直线平行，同旁内角互补).又因为∠1 =∠2.所以∠2 +∠3 = 180°.所以 AB∥DC (同旁内角互补，两直线平行) .
[选自教材P110 练习]
1. 如图，点 A 在直线 l 上，如果∠B ＝ 75°，∠C ＝ 43°.（1） 当∠1 ＝_____时， 直线 l ∥ BC；（2） 当∠2 ＝_____时， 直线 l ∥ BC.
[选自教材P110 练习]
2. 如图，∠ADE =∠DEF，∠EFC +∠C = 180°， 试问 AD 与 BC 平行吗？为什么？
解: 因为 ∠ADE =∠DEF ，所以 AD∥EF (内错角相等，两直线平行).又因为∠EFC +∠C = 180°，所以 EF∥BC (同旁内角互补，两直线平行).所以 AD∥BC (平行于同一条直线的两条直线平行).
1. 如图所示，下列条件中不能判定 DE∥BC 的是（ ）A. ∠1 =∠CB. ∠2 =∠3C. ∠1 =∠2D. ∠2 +∠4= 180°
2. 如图，一个弯形管道 ABCD 的拐角∠ABC = 120°，∠BCD = 60°， 这时说管道 AB∥CD 对吗？为什么？
解：管道 AB∥CD 是对的.理由: 因为∠ABC = 120°，∠BCD = 60°，所以∠ABC +∠BCD = 180°.所以 AB∥CD (同旁内角互补，两直线平行).
3. 如图所示，∠ABC = 90°，∠BCD = 90°，∠1 =∠2，那么 EB∥CF 吗？为什么？
解：EB∥CF，理由如下：因为∠ABC =∠BCD = 90°，所以∠1+∠3 =∠2+∠4 = 90°.因为∠1 = ∠2，所以∠3 = ∠4，所以 EB∥CF (内错角相等，两直线平行).
4. 已知：如图，∠ABC = 90°，∠1＋∠2＝90°，∠2＝∠3. BE∥DF 吗？为什么？
解 : BE∥DF.理由：因为∠1＋∠2＝90°，∠2＝∠3，所以∠1＋∠3＝90°又因为∠ABC = 90°，所以∠3 ＋∠4＝90°所以∠1 ＝∠4所以 BE∥DF (同位角相等，两直线平行).
5.如图所示，BE 是∠ABD 的平分线，DE 是∠BDC 的平分线，且∠1+∠2=90°，那么直线 AB，CD 的位置关系如何？并说明理由.
解：AB∥CD. 理由如下：因为BE是∠ABD的平分线，DE是∠BDC的平分线，所以∠ABD = 2∠1，∠BDC = 2∠2.又因为∠1+∠2 = 90°，所以∠ABD +∠BDC = 180°，所以 AB∥CD (同旁内角互补，两直线平行).
判定方法 1 同位角相等，两直线平行．
判定方法 2 内错角相等，两直线平行．
判定方法 3 同旁内角互补，两直线平行．