初中数学北师大版（2024）八年级下册4 分式方程多媒体教学ppt课件

这是一份初中数学北师大版（2024）八年级下册4 分式方程多媒体教学ppt课件，共23页。PPT课件主要包含了学习目标1分钟，例1解方程，最小公倍数6，例2解方程，解方程，最后一定要验根，原方程的分母为零，增根的定义，检验的方法，自学检测28分钟等内容，欢迎下载使用。
1.掌握分式方程的解法,及验根的方法;2.了解产生增根的原因，明确解分式方程必须验根。
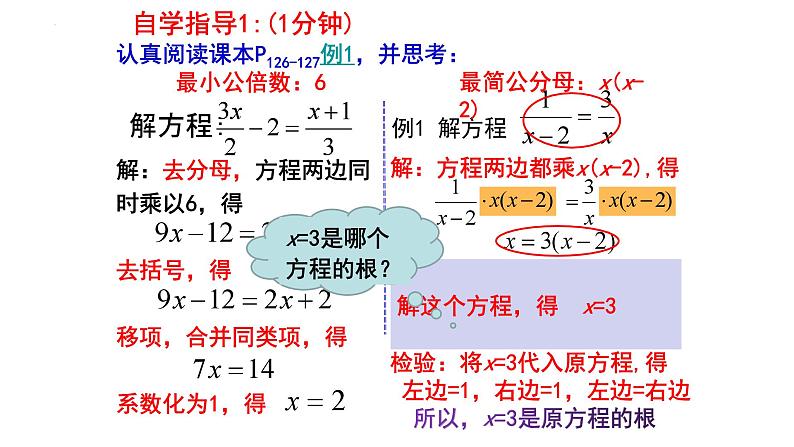
解：去分母，方程两边同时乘以6，得去括号，得移项，合并同类项，得系数化为1，得
解：方程两边都乘x(x-2),得 去括号,得 x=3x-6移项,合并同类项,得 -2x=-6系数化为1,得 x=3检验：将x=3代入原方程,得 左边=1，右边=1，左边=右边 所以，x=3是原方程的根
最简公分母：x(x-2)
自学指导1:(1分钟)
认真阅读课本P126-127例1，并思考：
解这个方程，得 x=3
解：方程两边都乘以x(x-2) 得 x=3(x-2)解这个方程，得 x=3经检验：x=3是原方程的根
去分母时，先找出各分母的最简公分母，再将方程两边各项都乘以最简公分母。
检验时，把未知数的值代入原方程，看等号是否成立。
关键：分式方程 整式方程
自学课本P127“例2”，思考：
解：方程两边都乘以2x，得 960-600=90x 解这个方程，得 x=4经检验，x=4是原方程的根
1.解分式方程的关键：
把分式方程化成整式方程
2.解分式方程的基本步骤：
自学检测1：（7分钟）
1.解分式方程 时，方程的两边需要同时乘以（　　）A．2x﹣4B．xC．2x（x﹣2）D．2x（x+2）2.把方程 去分母后的形式为( ) A.1+3=x-1 B.-1+3=x-1 C.-1+3(x-2)=x-1 D.1+3(x-2)=x-1
方程两边都乘以2x-3得： x-5=4(2x-3)解得： x=1经检验：x=1是原方程的根。
学生讨论、更正，教师点拨（2分钟）
(易错点)去分母时注意符号的变化.
(易漏点)去分母时注意不要漏乘.
解分式方程时，首先要去分母化为整式方程.
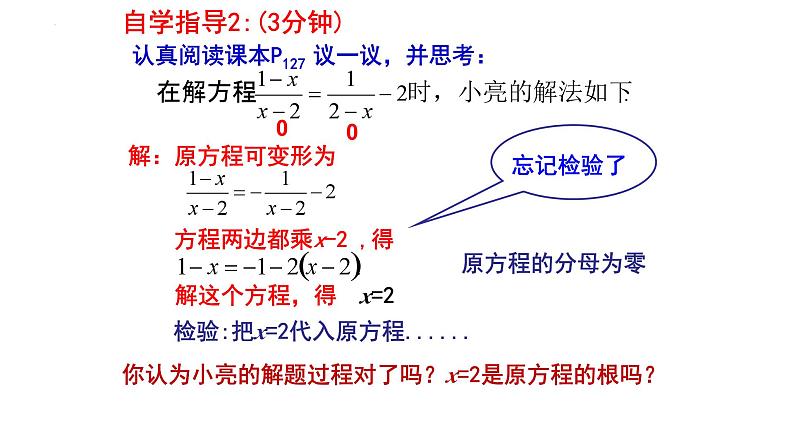
解：原方程可变形为 方程两边都乘x-2 ,得
你认为小亮的解题过程对了吗？x=2是原方程的根吗？
检验:把x=2代入原方程
自学指导2:(3分钟)
认真阅读课本P127 议一议，并思考：
解这个方程，得 x=2
解：原方程可变形为 方程两边都乘x-2 ,得 解这个方程，得 x=2
产生增根的原因,是我们在方程的两边同乘了一个使分母为零的整式.
使得原分式方程的分母为零的根，我们称它为原方程的增根。所以原方程无解。
经检验，x＝2是原方程的增根。所以原方程无解。
这里的检验要以计算正确为前提
切记：解分式方程一定要验根！
方法1：把解直接代入原方程进行检验(一般方法)方法2：把解代入分式的最简公分母，看最简公分母的值是否为零，若等于零，即为增根(最简方法）
解：两边同乘以(x-2)得， 1+3（x-2)=x-1 解得，x=2 经检验，x=2是原方程的增根， ∴原方程无解
2.已知关于x的方程 有增根，增根是＿＿＿，则k=_________，
解：去分母得：2x²-9=kx+2k ∵方程有增根，∴ x=±2 当x=-2时，8-9=-2k+2k ,-1=0不成立
分式方程有增根（解题步骤）：①将分式方程化成整式方程②令最简分母＝0，求增根③将增根代入整式方程，并求出所求字母的值
1.分式方程若有增根，则增根可能是——————————————
使分母为0的未知数的值
解：两边同乘以（x+1)(x-1) 得， x+1=2 解得，x=1检验：把x=1代人最简公分母 得（x+1)(x-1)=0所以x=1是原方程的增根， 原方程无解。
解：两边同乘以(x-2)得， 1+3（x-2)=x-1 解得，x=2检验：把x=2代人最简公 分母得,(x-2)=0 所以x=2是原方程的增根， 原方程无解。
2、解分式方程的基本步骤是：
（2）代入最简公分母。
经检验：x=1是原方程的增根所以原方程无解。
经检验：x=2是原方程的增根所以原方程无解。
1、化：即在方程两边都乘以最简公分母。约去分母，化成整式方程。
解分式方程的一般步骤：（易错点）
2、解：解这个整式方程。
3、检验：把整式方程的根代入最简公分母，看结果是否是零，使最简公分母为零的根，是原方程的增根，必须舍去。
注意：不要漏乘不含分母项。
2.若分式 与 的值互为相反数，则x＝（　　）A．﹣2.4 B． C．﹣8D．2.4
3.若关于x的分式方程 + ＝2有增根，则m的值为___________．
4.关于x的分式方程 + ＝1的解为非正数，则k的取值范围是____________　．
解：方程两边都乘以（2x+1）(2x-1)得： 2（2x+1)-4=0解得：x=经检验：x= 是原方程的增根，所以原方程无解。
方程两边都乘以x-4得： 3-x-1=x-4解得： x=3经检验：x=3是原方程的根。
6、已知关于 x 的方程
①如果此方程有增根，那么增根是______ .
②当m为何值时，此方程有增根？
所以，当m=-1时此方程有增根
若方程 无解，则m=_____.
解：去分母得：mx+1-x=0 即 (m-1)x=-1 ∵方程无解，故有两种情况： ②当m-1=0时，方程无解，则m=1
分式方程无解可能有两种情况：①将分式方程化为整式方程后，求出x是分式方程的增根②所化成的整式方程无解，导致原方程无解
根据分式方程根的正负求字母的取值范围：“分式的分母不能为零”是隐含条件。解题思路：既要考虑分式方程的解的正负性，也要确保最简公分母不为零
P128知识技能T1(1)(2)
解：方程两边都乘以x(x+1)得： 6x=x+5解得：x=1经检验：x=1是原方程的根所以原方程的解为x=1。
解：方程两边都乘以x-4得： 3-x-1=x-4解得：x=3经检验：x=3是原方程的根所以原方程的解为x=3。