初中数学北师大版（2024）八年级下册2 提公因式法说课ppt课件

这是一份初中数学北师大版（2024）八年级下册2 提公因式法说课ppt课件，共19页。PPT课件主要包含了学习目标1分钟，自学检测16分钟，注意结果的形式，自学检测28分钟，把下列各式分解因式，易错点不变号而出错，互为相反数，b-an，-b-an，a+bn等内容，欢迎下载使用。
4.2.2 提公因式法
1、能够熟练地运用提公因式法把多项式分解 因式。2、理解提公因式法与多项式乘以多项式之间的关系。
学生自学，教师巡视（4分钟）
阅读课本P97例题2，并思考：
点拨：由例题可知提公因式时，公因式可以是多项式
自学指导1：(1分钟)
认真阅读例题2，注意解题格式
例2 把下列各式因式分解
（1）a(x-3)+2b(x-3)
(2)y(x+1)+y²(x+1)²
解：原式=(x-3)(a+2b)
解：原式=y(x+1)[1+y(x+1)] =y(x+1)(xy+y+1)
在（1）中，公因式是（x-3）
在（2）中，公因式是 y(x+1)
下列各式因式分解(P98 习题4.3 T1）（3）2(m-n)2-m(m-n)
解：原式= (m-n)[2(m-n)-m]
= (m-n) (m-2n)
解：原式=(a²+b²) (m+n)
解：原式=(2a+b)(2a-3b-3a) =(2a+b)(-a-3b) =-(2a+b)(a+3b)
（5）m(a²+b²)+n(a²+b²)
（7）(2a+b)(2a-3b)-3a(2a+b)
多项式各项的公因式是多项式时，要把它看成一个整体，可以用提公因式法进行因式分解。
（4）x(x-y)2-y(y-x)2
解：原式= x(x-y)2-y(x-y)2
= (x-y)2（x-y）
= (x-y)3
学生自学，教师巡视（5分钟）
自学指导2：(1分钟）
2、添括号时，括号前面是“+”号，括号里的各项符号________,
添括号时，括号前面是“-”号，括号里的各项符号________, (改变或不变)
1、（第97页做一做）请在下列各式等号右边的括号前填入“+”或“－”号，使等式成立：
（1）2-a=___(a-2)； （2）y-x=___(x-y);
（3）b+a=___(a+b)； （4）(b-a)2 =___(a-b)2 ;
（5）-m-n=__(m+n)； （6）-s2+t2=__(s²-t²).
阅读第97页内容，认真学习例3，并完成做一做，将答案填写在课本上。
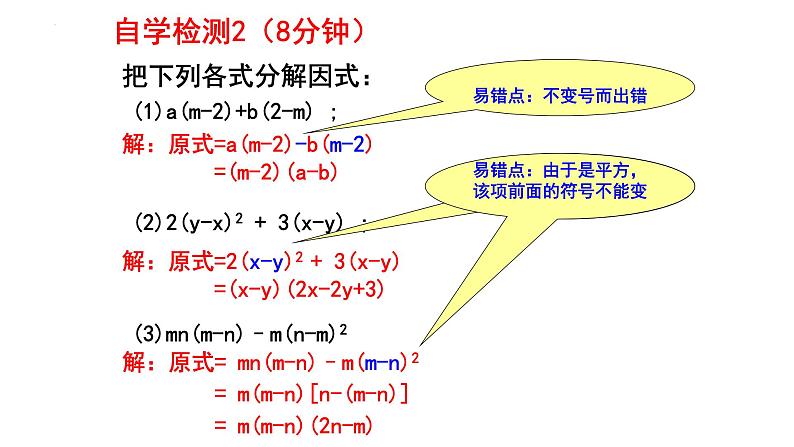
(1)a(m-2)+b(2-m) ;(2)2(y-x)2 + 3(x-y) ; (3)mn(m-n)–m(n-m)2
解：原式=a(m-2)-b(m-2) =(m-2)(a-b)
解：原式=2(x-y)2 + 3(x-y) =(x-y)(2x-2y+3)
解：原式= mn(m-n)–m(m-n)2 = m(m-n)[n-(m-n)] = m(m-n)(2n-m)
(1)a-b 与 b-a.
(a-b)n =______(n是偶数） (a-b)n = ________(n是奇数）
（2）a+b 与 -a-b
(-a-b)n =______(n是偶数）(-a-b)n =_______(n是奇数）
讨论、更正、点拨（3分钟）
讨论：下列各组代数式是什么关系？
(变式2)下列式子从左到右的变形，错误的是（ ）
A、(y-x)²= (x-y)² B、-a-b=-(a+b)C、 (a-b)³= -(b-a)³ D、-x+y=-(x+y)
（变式1） （x-y） =___（y-x） （x-y）² =____（y-x）² （m-n）³ =____（n-m）³
(1)(y-x)² = -(x-y)² (2)(3+2x)³= -(2x+3)³(3)a-2b = -(-2b+a) (4) -a+b = -(a+b)(5)(a-b)(x-2y) = (b-a)(2y-x)
2.在下列各式右边括号前添上适当的符号,使左边与右 边相等.(1) a+2 = ___(2+a) (2) -x+2y = ___(2y-x)(3) (m-a)2 = ___(a-m)2 (4) (a-b)3 = ___(-a+b)3(5) (x+y)(x-2y)= ___(y+x)(2y-x)
1.判断下列各式是否正确?
1、在提取公因式时，各项公因式相同时，直接提取；各项公因式互为相反数时，需先变符号，再提取。2、括号前面是“+”号，括号里的各项都不变号3、括号前面是“-”号，括号里的各项都变号
4、用提公因式法分解的口诀：
找准公因式，一次要提净；
全家都搬走，留 1 把家守；
提负要变号，变形看奇偶。
两个只有符号不同的多项式是否有关系,有如下判断方法:(1)当相同字母前的符号相同时, 则两个多项式相等. 如: a-b 和 -b+a 即 a-b = -b+a (2)当相同字母前的符号均相反时, 则两个多项式互为相反数. 如: a-b 和 b-a 即 a-b = -(a-b)
(1)a-b 与 -a+b 互为相反数.
(a-b)n = (b-a)n (n是偶数） (a-b)n = -(b-a)n (n是奇数）
(2) a+b与b+a 为相同数.
(a+b)n = (b+a)n (n是整数）
a+b 与 -a-b 互为相反数.
(-a-b)n = (a+b)n (n是偶数） (-a-b)n = -(a+b)n (n是奇数）
2、因式分解：课本P98习题4.3 T1（5）（6）（7）（8）
1、下列各式正确的有（ ） A. (y-x)2 = -(x-y)2 B. (3+2x)3 = -(2x+3)3 C. a-2b = -(-2b+a) D. (a-b)(x-2y) = (b-a)(2y-x)
（选做题）课本P98习题4.3 T2（1）
(选做题)课本P98习题4.3 T2（1）先分解因式，再计算求值：
2、（课本P98习题4.3 T1）把下列各式分解因式：
解：原式=x(m-2)(10-3m) 当x=1.5，m=6时， 原式=1.5×(6-2)(10-3×6) =-48
解：原式=(a2+b2)(m+n)
解：原式= 6(a-b)2(3a-5b)
解：原式= -2xy(x+y)
注意解题格式①将原式化简②当……时， 代入最简式中计算。
解：原式= -(2a+b)(a+3b)
（课本P98习题4.3 T3）
解：(a+b)2+a(a+b)+(a+b)b =(a+b)(a+b+a+b) =(a+b)(2a+2b) =2(a+b)2
答：这三块草坪的总面积是2(a+b)2
（选做题）1、分解因式：
2、已知1+x+x²+x³+x4=0，求1+x+x²+x³+…+x2019的值
(1)3a( a–b )2 + 6ab ( b–a )
1、解：原式 = 3a( a–b )2–6ab( a–b ) = 3a( a–b ) [ ( a–b )–2b ] = 3a( a–b ) ( a–b–2b) = 3a( a–b )( a–3b) = 3a( a–b )( a–b )
解：原式=6(m-n)3 -12(m-n)²
P97例3 把下列各式因式分解：
(1) a(x-y)+b(y-x)
解：原式=a(x-y)-b(x-y) =(x-y)(a-b)
(2) 6(m-n)³-12(n-m)²
=6(m-n)2(m-n-2)