2024~2025学年湖北省武汉市硚口区九年级上期中数学试卷（解析版）

这是一份2024~2025学年湖北省武汉市硚口区九年级上期中数学试卷（解析版），共22页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1. 我国民间建筑装饰图案中，蕴含着丰富数学之美．下列图案中既是轴对称图形又是中心对称图形的是（ ）
A. B. C. D.
【答案】A
【解析】解：A．该图形是轴对称图形，也是中心对称图形，故此选项正确；
B．该图形不是轴对称图形，但是中心对称图形，故此选项错误；
C．该图形不是轴对称图形，也不是中心对称图形，故此选项错误；
D．该图形是轴对称图形，但不是中心对称图形，故此选项错误．
故选：A．
2. 已知m和n分别为一元二次方程的两个不相等的实数根，则的值为（ ）
A. 2B. C. 4D.
【答案】C
【解析】解：和分别为一元二次方程的两个不相等的实数根，
．
故选：C．
3. 如图，点，，，，都在方格纸的格点上，若可以由旋转得到，则正确的旋转方式是（ ）

A. 绕点逆时针旋转B. 绕点顺时针旋转
C. 绕点逆时针旋转D. 绕点逆时针旋转
【答案】C
【解析】解：根据图形可知：，
∴图形是以为旋转中心，旋转90°后和重合，和重合，和重合，
∵可以由旋转得到，
∴正确的旋转方式是绕点逆时针旋转90°，
故选C．
4. 将抛物线平移后得到抛物线，正确的平移方式是（ ）
A. 向右移动3个单位长度，向上移动1个单位长度
B. 向左移动3个单位长度，向上移动1个单位长度
C. 向右移动3个单位长度，向下移动1个单位长度
D. 向左移动3个单位长度，向下移动1个单位长度
【答案】D
【解析】将抛物线平移后得到抛物线，
正确的平移方式是向左移动3个单位长度，向下移动1个单位长度．
故选：D．
5. 关于的一元二次方程有两个不相等的实数根，则的取值范围是（ ）
A. B. C. D.
【答案】A
【解析】解：∵关于的一元二次方程有两个不相等的实数根，
∴，
解得：，
∴的取值范围是．
故选：A．
6. 如图，经过点，交y轴于点B，若，则点B的纵坐标是（ ）
A. B. C. D.
【答案】C
【解析】解：如图，作轴交y轴于点C，
，轴，
，，
，
由图可知，点B在y轴的负半轴上，则点B的纵坐标是．
故选：C．
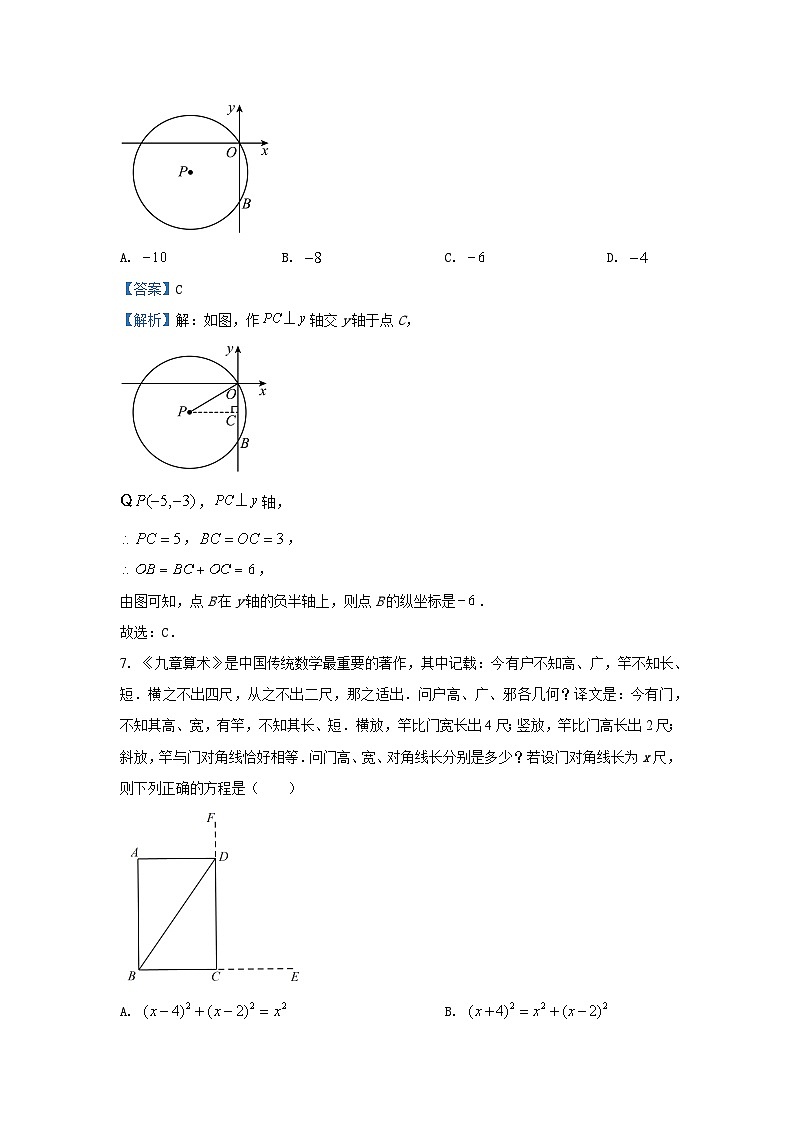
7. 《九章算术》是中国传统数学最重要的著作，其中记载：今有户不知高、广，竿不知长、短．横之不出四尺，从之不出二尺，那之适出．问户高、广、邪各几何？译文是：今有门，不知其高、宽，有竿，不知其长、短．横放，竿比门宽长出4尺；竖放，竿比门高长出2尺；斜放，竿与门对角线恰好相等．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则下列正确的方程是（ ）
A. B.
C. D.
【答案】A
【解析】解：∵设门对角线长为x尺，
∴竿的长度为x尺，门高为尺，门宽为尺，
根据题意得：，
故选：A．
8. 如图，要修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安一个喷水头，使喷出的抛物线形水柱在与池中心的水平距离为处达到最高，且最高高度为，水柱落地处离池中心，则水管的长是（ ）
A. B. C. D.
【答案】C
【解析】解：由题意可知点是抛物线的顶点，
∴设这段抛物线的解析式为．
∵该抛物线过点，
∴，
解得：．
∴．
∵当x=0时，，
∴水管应长．
故选：C．
9. 如图，将绕点A顺时针旋转，得到，连接．若，，则的大小是（ ）
A. B. C. D.
【答案】C
【解析】设，
将绕点A顺时针旋转，得到，
，，
，
为等边三角形，
，
，
，
，
故选：C．
10. 已知，两点在抛物线上（常数），若对于，，都有，则a的值不可能是（ ）
A. B. C. D.
【答案】B
【解析】解：由题得，，
，
，
，
①当时，，
或，
解得或，
，
或，
或，
，
；
②当时，，
或，
解得，
，
，解得，
综上，或．
故选：B．
二、填空题（共6小题，每小题3分，共18分）
11. 已知点与点关于原点O中心对称，则m的值是________．
【答案】
【解析】解：∵点与点关于原点O中心对称，
∴，
解得，，
故答案为：．
12. 将一元二次方程化为一般形式后，常数项是1，则一次项系数是________．
【答案】
【解析】解：∵，
∴，
∴一次项系数是．
故答案为：．
13. 点绕点顺时针旋转后，得到对应点的坐标是________．
【答案】
【解析】解：如图，作点绕点顺时针旋转后的对应点，连接，作轴于，轴于，
由旋转的性质可知，，，
∴，即，
又∵，
∴，
∴，
∴，
故答案为：．
14. 某商场购进一种单价为40元的商品，如果以单价60元售出，那么每天可卖出300个，根据销售经验，每降价1元，每天可多卖出20个，设每个商品降价x（元），每天获得利润y（元），则y与x的函数关系式是________．
【答案】
【解析】解：设每个商品降价x（元），每天获得利润y（元），
则y与x的函数关系式是：，即，
故答案为：．
15. 如图，正方形的边长为，，平分交的延长线于，交CD于．当为CD的中点时，的长是______．
【答案】
【解析】解：过点作于点，交AD于点，连接CE交BM于点，连接，
∵正方形的边长为，，为CD的中点，
∴，，，
∴，，
∵平分，
∴，，，
∴，
∵，，
∴，
∴，
∴，
∴，
∵，
∴，
∴，
解得，
∴，
∵，
∴四边形是矩形，
∴，，，
∴，
∴，
故答案为：．
16. 抛物线（a，b，c为常数）经过点，且．
下列四个结论：
①；
②当时，；
③若点，均在抛物线上，则；
④不等式对任意的实数t都成立，则．
其中正确的结论是________（填写序号）．
【答案】①③④
【解析】解：∵抛物线经过，
∴，
故①正确，符合题意；
当时，如图1，此时当时，，
当时，如图2，此时两个交点均在y轴左侧，都有可能是，
但是不论哪个交点是，均不满足当时，，
故②错误，不符合题意；
根据题意可得，
，
消去a和b整理可得，
∵，
，
解得：，
故③正确，符合题意；
∵，
∴，
∴，
∴当时函数有最小值，即抛物线开口向上，对称轴为直线，
，，
，
由，可得，
，
故④正确，符合题意；
故答案为：①③④；
三、解答题（共8小题，共72分）
17. 解方程：．
解：，
∵ ，，，
∴
∴，
∴,．
18. 如图，在中，，将绕点A逆时针旋转得到，点C的对应点E落在上．
（1）若，，求的长；
（2）连接，在中，添加与角相关的一个条件，使是等边三角形．（不需要说明理由）
解：（1）在中，，，
∴．
∵由旋转得到
∴，
∴，
∴．
（2）添加：（或），理由如下：
由旋转可得：，
∵，
∴为等边三角形．
19. 如图，在等腰中，，交于，两点，半径于．
（1）求证：；
（2）若，，求的半径．
解：（1）证明：在中，，于，
，
是的弦，是半径，且于，
，
，
；
（2）解：如下图所示，连接AD，
由（1）知，，
设半径为，则，
在中，，
解得：，
的半径为．
20. 如图，某植物园有一块足够大的空地，用一段长为米的篱笆围成一个一边利用一堵墙的矩形花圃，墙长为6米，其中边AD大于或等于墙长，中间用篱笆隔开．设的长为x米，AB的长为y米，矩形花圃的面积为s米．

（1）直接写出y关于x，s关于x的函数关系式以及自变量x的取值范围；
（2）当的长为多少时，矩形花圃的面积最大？最大面积为多少？
解：（1）由题意知，，，
整理得，，
∵，
∴，则，
由题意知，，
∴，，；
（2）由题意知，．
∵，
∴当时，取得最大值，且最大值为，
答：当的长为9米时，矩形花圃的面积最大，且最大面积为平方米．
21. 如图是由小正方形组成的网格，每个小正方形的顶点叫做格点．的三个顶点都是格点，仅用无刻度的直尺在给定网格中完成画图．
（1）在图1中，D在线段上，先画，再在AB上画点F，使；
（2）在图2中，先画的高，再在射线上画点P，使．
解：（1）如图1，点向右3个格点为，连接，
∵，
∴四边形为平行四边形，
∴即为所作；
如图1，连接，记的中点为，连接并延长到，连接，交于，则四边形为矩形，
∴，
∴，
∴点即为所作；
（2）如图2，点向左4个格点为，然后向上3个格点为，连接，交于，

∵，
∴，
∴，
∴，
∴，
∴，
∴即为所作；
如图2，点向左3个格点为，点向左3个格点为，连接，的交点为，连接，
∴，且到的距离与的距离相等，即，
∴垂直平分，
∴，
∴，
∵，
∴，
∴，
∴点即为所作．
22. 图1展示的发石车是古代一种攻城器械，据《三国志》记载：曹操创制发石车，攻破袁绍军壁楼．如图，发石车位于点处，其前方有一堵壁楼，其防御墙的竖直截面为矩形，墙宽为米，点与点的水平距离为米，垂直距离为米．以点为原点，水平方向为轴方向，建立平面直角坐标系，将发射出去的石块当作一个点看，其飞行路线可以近似看作抛物线的一部分．
（1）若发射石块在空中飞行的最大高度为米．
①求抛物线的解析式（不用写出的取值范围）；
②石块能否飞越防御墙．
（2）若要使石块恰好落在防御墙顶部上（不包括端点，，直接写出的取值范围．
解：（1）①设石块运行的函数关系式为，
将代入，得，解得．
所以抛物线的解析式为．
②石块不能飞跃防御墙．
理由如下：将代入，；
将代入，．所以石块不能飞跃防御墙．
（2）∵过点，
∴，
∴，
∴，
依题意分别代入，
即或，
解得： 或，
∴．
23. 问题情境 是等边的中线，点P在线段上运动（不包括端点C，D），将线段绕点P顺时针旋转，点A的对应点E落在射线上，探究的大小．记．
问题探究
（1）如图1，将问题特殊化，当时，直接写出的大小；
（2）如图2，将问题一般化，当时，求证：是定值．
问题拓展
（3）当时，若，直接写出的值．
解：（1）解：∵是等边三角形，
∴，
∵是等边的中线，
∴平分，
∴，
∴．
（2）证明：连接，过点P作于H．
∵是等边的高，
∴是的垂直平分线，
∴，；
∵线段绕点P顺时针旋转得到，
∴，
∴．
∴垂直平分，即．
在中，，
∴，
∴，
∴．
∴．
（3）解：连接，过点P作于H．
同（2）可知：，
∵，
∴，
∴，
∵，
∴，，
∴，
∴，，
∵，，
∴．
24. 如图1，抛物线交x轴于，B两点，交y轴于点C．
（1）直接写出直线和抛物线的解析式；
（2）设直线与抛物线交于D，E两点（D在E左边），与射线交于点F，若，求m的值；
（3）如图2，点M在第四象限的抛物线上运动，点N与点M关于y轴对称，直线分别交直线，x轴于P，Q，G三点，若，求t的值．
解：（1）∵抛物线交x轴于，
∴，
∴，
∴，
当时，；
当时，或，
∴，B4,0，
设直线的解析式为，
则，
解得，，
∴直线的解析式为．
（2）设直线与y轴交于点G，
则点F的坐标为．
当时，
∵，
∴，
∴由中点坐标得点E的坐标为．
∴，
整理得，
解得或（舍去）；
当时，
∵，
∴，
∴点E的坐标为．
∴，
整理得，
解得或（舍去）．
综上所述，m的值为3或．
（3）设点M的坐标为，
则点N的坐标为，
而，
设直线的解析式为，
则，
解得，
∴．
与直线联立，
得点P的坐标为，
同理，可得直线解析式为：，
点Q的坐标为．
当时，，
由，
解得；
当时，，
由，
解得．

综上所述，t的值为3或5．