北师大版（2024）七年级下册（2024）3 乘法公式课文内容ppt课件

这是一份北师大版（2024）七年级下册（2024）3 乘法公式课文内容ppt课件，共31页。PPT课件主要包含了学习目标，新课导入，新知探究，完全平方公式，两数的平方和，直接求，总面积，a+b2，间接求，a2+等内容，欢迎下载使用。
1.经历探索完全平方公式的过程，进一步发展符号感和推理能力。【重点】2.会推导完全平方公式，并能运用公式进行简单的计算。【难点】
计算：(1)(x＋1)2； (2)(y－2)2。解：(1)原式＝(x＋1)(x＋1)＝x2＋x＋x＋1＝x2＋2x＋1。  　　　　(2)原式＝(y－2)(y－2)＝y2－2y－2y＋4＝y2－4y＋4。思考：由上述计算，你发现了什么结论？
发现：原式是两数和(或差)的平方，结果是这两数平方和与它们2倍的和(或差)。
知识点 完全平方公式
探究：计算(a＋b)2，(a－b)2，并归纳计算结果。
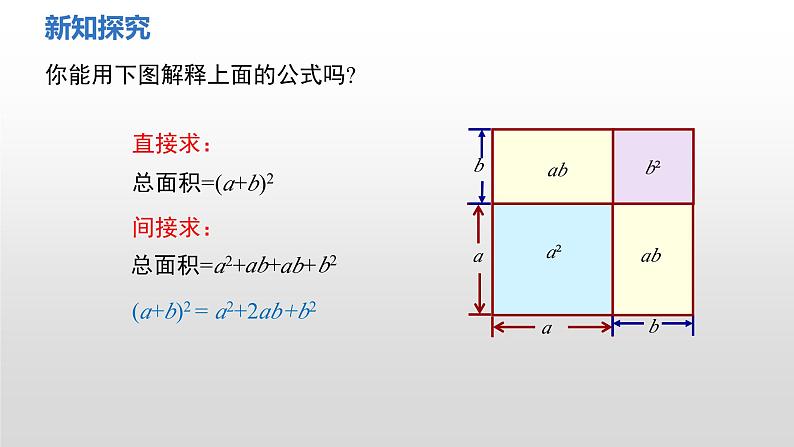
解：(a＋b)2＝(a＋b)(a＋b) ＝a2＋ab＋ab＋b2 ＝a2＋2ab＋b2。
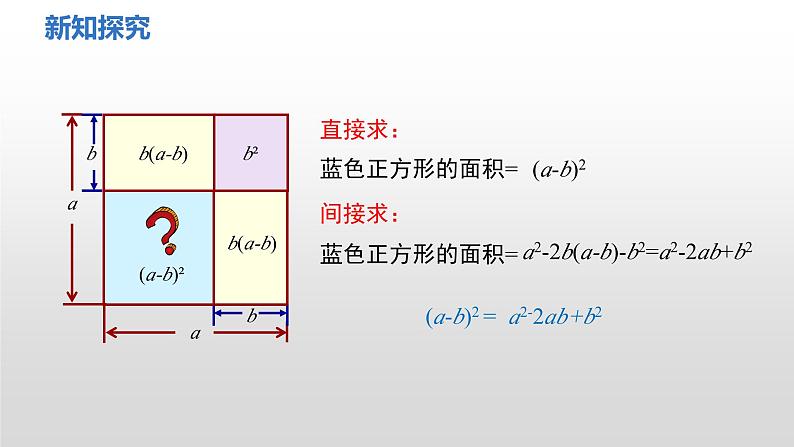
(a－b)2＝(a－b)(a－b) ＝a2－ab－ab＋b2 ＝a2－2ab＋b2。
两数和（或差）的平方，等于 加上（或减去）两数积的 。
简记为：“首平方，尾平方，积的2倍放中间”。
你能用下图解释上面的公式吗?
a2-2b(a-b)-b2=a2-2ab+b2
完全平方公式的特征：1. 积为二次三项式；2. 积中的两项为两数的平方；3. 另一项是两数积的 2 倍，且与原式中间的符号相同；4. 公式中的字母 a，b 可以表示数、单项式和多项式。
利用完全平方公式计算：(1)(5－a)2； (2)(－3m－4n)2；(3)(－3a＋b)2； (4)(a＋b＋c)2。解：(1)(5－a)2＝25－10a＋a2。(2)(－3m－4n)2＝9m2＋24mn＋16n2。(3)(－3a＋b)2＝9a2－6ab＋b2。(4)原式＝(a＋b)2＋2(a＋b)c＋c2＝a2＋2ab＋b2＋2ac＋2bc＋c2。
注意：当公式中的两个数的系数绝对值不为1时，平方时不要漏掉系数的平方。
思考：(a+b)2与(-a-b)2 相等吗?(a-b)2与(b-a)2相等吗?(a-b)2与a2-b2相等吗?为什么?解：(-a-b)2=(-a)2-2·(-a)·b+b2=a2+2ab+b2=(a+b)2。(b-a)2=b2-2ba+a2=a2-2ab+b2=(a-b)2。(a-b)2与a2-b2不一定相等，只有当b=0或a=b时，(a-b)2=a2-b2。
(x＋y)2 =x2＋2xy＋y2
 (x－y)2 =x2－2xy＋y2
(－x＋y)2 =x2－2xy＋y2
(2x＋y)2 =4x2＋4xy＋y2
如果36x2＋mxy＋25y2是一个完全平方式，求m的值。解：因为36x2＋mxy＋25y2＝(6x)2＋mxy＋(5y)2，所以mxy＝±2·6x·5y，所以m＝±60，所以m＝60或－60。
注意：完全平方式要分清是哪两数的平方和加上或减去它们积的2倍，已知完全平方式求中间系数中字母值时要考虑两种情况。
知识点 完全平方公式的几何意义
我们已经接触了很多代数恒等式，知道可以用一些硬纸片拼成的图形面积来解释一些代数恒等式．例如图甲可以用来解释(a＋b)2－(a－b)2＝4ab。那么通过图乙面积的计算，验证了一个恒等式，此恒等式是(　 　)
A．a2－b2＝(a＋b)(a－b)B．(a－b)(a＋2b)＝a2＋ab－2b2C．(a－b)2＝a2－2ab＋b2D．(a＋b)2＝a2＋2ab＋b2
结果是三项，不要漏掉中间项
(a±b)2=a2±2ab+b2
两数和(或差)的平方，等于它们的平方和，加上(或减去)它们积的2倍
图形变形前后阴影部分面积相等
1.若x＋y＝4，则x2＋2xy＋y2的值是(　　) A．2　　　　　　B．4　　　　　　C．8　　　　　　D．162.如图，从边长为(a+1)cm的正方形纸片中剪去一个边长为(a﹣1)cm的正方形(a＞1)，剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙)，则该矩形的面积是(　　)A．2cm2    B．2acm2 C．4acm2 D．（a2﹣1）cm2
3.若(3x－b)2＝ax2－12x＋4，则a，b的值分别为(　　) A．3，2     B．9，2     C．3，－2     D．9，－2
第4课时　完全平方公式的运用
北师大版-数学-七年级下册
1.综合运用平方差公式和完全平方公式进行乘法运算。【重点】2.准确分辨并利用乘法公式进行运算。【难点】
有一位老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们。来一个孩子，老人就给这个孩子一块糖；来两个孩子，老人就给每个孩子两块糖；来三个，就给每人三块糖；…… 第一天，有a个男孩一起去了老人家，老人一共给了这些孩子____块糖； 第二天，有b个女孩一起去了老人家，老人一共给了这些孩子____块糖； 第三天，这(a+b)个孩子一起去看老人，老人一共给了这些孩子_______块糖。 问：这些孩子第三天得到的糖果数与前两天他们得到的糖果总数哪个多？多多少？为什么？
孩子们前两天得到的糖果总和为：a2＋b2。    第三天得到的糖果数为：(a＋b)2＝a2＋2ab＋b2。所以(a＋b)2－(a2＋b2)＝a2＋2ab＋b2－a2－b2＝2ab。
解：(1)原式＝(100－1)2 ＝1002－2×100×1＋1＝9 801。     
知识点 完全平方公式的运用
探究：怎样计算992，4012更简单呢？ (1)992；                   (2)4012。
(2)原式＝(400＋1)2＝4002＋2×400×1＋1＝160 801。
解：(1)原式＝(100＋2)2=10 000＋400＋4=10 404。
例1 运用完全平方公式计算： (1)1022；       (2)1972。
(2)原式＝(200－3)2=40 000－1 200＋9=38 809。
知识点 公式法的综合运用
例2 计算：(1)(3x－2y)2＋(3x－2y)(－2y－3x)；解：原式＝9x2－12xy＋4y2＋4y2－9x2 ＝8y2－12xy。(2)(x－1＋y)(x＋1＋y)；解：原式＝[(x＋y)－1][(x＋y)＋1] ＝(x＋y)2－1 ＝x2＋2xy＋y2－1。
(3)4(a＋2)2－7(a＋3)(a－3)＋3(a－1)2。解：原式＝4(a2＋4a＋4)－7(a2－9)＋3(a2－2a＋1) ＝4a2＋16a＋16－7a2＋63＋3a2－6a＋3 ＝10a＋82。
【方法总结】 运用平方差公式计算(2)(x－1＋y)(x＋1＋y)时要注意分组方法，将括号内不变号的项作第一项，变号项作为第二项，然后利用平方差公式计算。运用完全平方公式时要注意乘积的2倍项的符号。　　
用乘法公式计算：(1)(a－b＋3)(a＋b－3)；解：原式＝[a－(b－3)][a＋(b－3)]＝a2－(b－3)2＝a2－b2＋6b－9。(2)(a＋b＋c)2；解：原式＝(a＋b)2＋2(a＋b)c＋c2＝a2＋2ab＋b2＋2ac＋2bc＋c2。(3)[(a－b)2－(a＋b)2]2。解：原式＝{[(a－b)＋(a＋b)][(a－b)－(a＋b)]}2 ＝[2a·(－2b)]2＝16a2b2。
【方法总结】完全平方公式的常见变式：x2＋y2＝(x－y)2＋2xy＝(x+y)2－2xy，(x－y)2＝(x+y)2－4xy。
已知a－b＝3，ab＝1，求a2＋b2及(a＋b)2的值。解：a2＋b2＝(a－b)2＋2ab＝9＋2＝11。 (a＋b)2＝a2＋b2＋2ab＝11＋2＝13。
知二求二:熟练掌握完全平方公式的常见变形
数式的简便计算:根据数式中数的特点选择乘法公式
整式的简便计算:根据整式中式子的特点选择乘法公式
1.利用整式乘法公式计算：(1)89.82；      解：(1)原式=(90－0.2)2=902－2×0.2×90＋0.22=8 064.04。(2)472－94×27＋272；(2)原式=472－2×47×27＋272=(47－27)2=202=400。(3)(a－b－3)(a－b＋3)。(3)原式=(a－b)2－32=a2－2ab＋b2－9。