湖北省武汉市常青联合体2024-2025学年高一上学期期末考试数学试卷 含解析

这是一份湖北省武汉市常青联合体2024-2025学年高一上学期期末考试数学试卷 含解析，共16页。试卷主要包含了单项选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。
命题学校：武汉市第十五中学 命题教师：徐煊 审题教师：冷秋君
考试时间：2025年1月15日 试卷满分：150分
一、单项选择题（本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）
1. 计算的值为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】利用三角函数诱导公式转化为特殊角三角函数值即可解决.
【详解】
故选：C
2. 函数的定义域为（ ）
A. B. C. D.
【答案】D
【解析】
【分析】由对数型复合函数定义域和分母不为零求解即可；
【详解】由题意得，解得且，
所以函数的定义域为，
故选：D.
3. 要得到函数的图象，只需将的图象（ ）
A. 向左平移个单位B. 向右平移个单位C. 向左平移个单位D. 向右平移个单位
【答案】D
【解析】
【分析】利用三角函数的图象变换关系求解.
【详解】,
所以要得到函数的图象，
只需将的图象向右平移个单位，
故选:D.
4. 设，，，则（ ）
A B. C. D.
【答案】D
【解析】
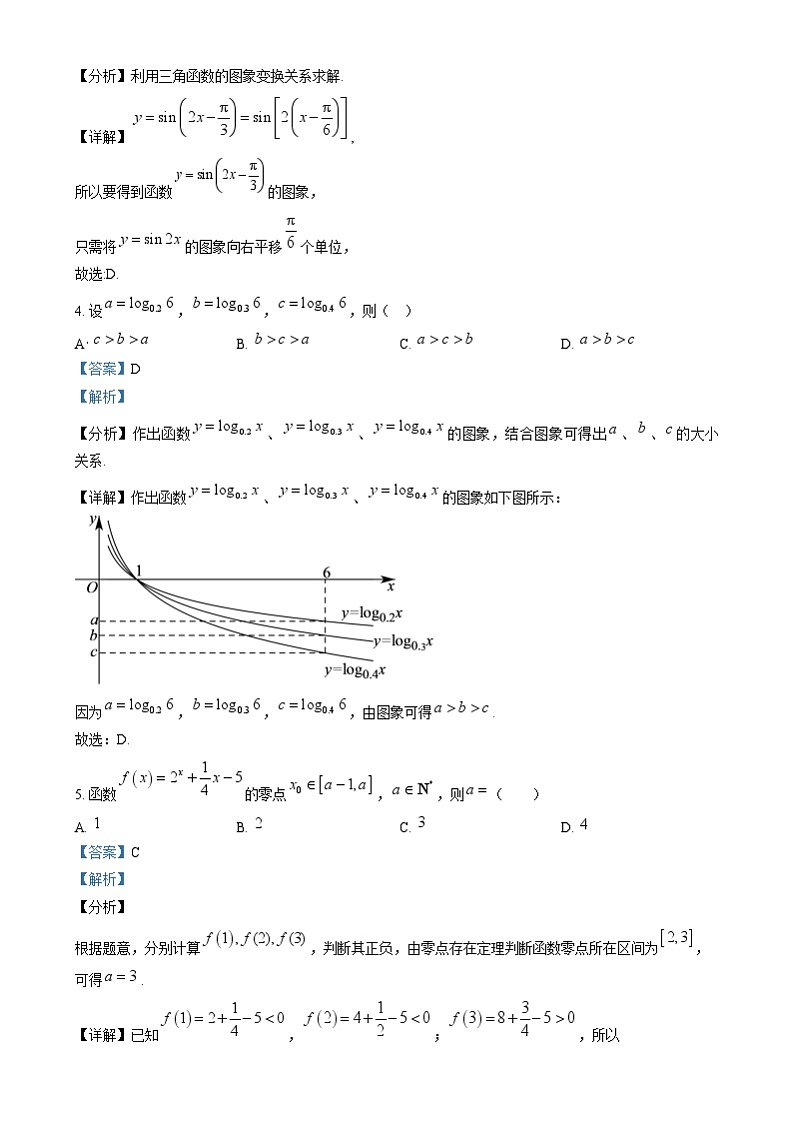
【分析】作出函数、、的图象，结合图象可得出、、的大小关系.
【详解】作出函数、、的图象如下图所示：
因为，，，由图象可得.
故选：D.
5. 函数的零点，，则（ ）
A. B. C. D.
【答案】C
【解析】
【分析】
根据题意，分别计算，判断其正负，由零点存在定理判断函数零点所在区间为，可得.
【详解】已知，；，所以，可知函数零点所在区间为，故.
故选：C.
6. 已知锐角，且，则（ ）
A. B. C. D.
【答案】D
【解析】
【分析】注意到，利用同角三角函数的关系求角的正弦，再利用诱导公式求角的正弦、余弦，从而得到的正切.
【详解】因为为锐角，所以且，所以得，
由诱导公式得，.
所以.
故选:D
7. “圆材埋壁”是我国古代的数学著作《九章算术》中的一个问题，现有一个“圆材埋壁”模型，其截面如图所示．若圆柱材料的截面圆的半径长为，圆心为，墙壁截面为矩形，且劣弧的长等于半径长的倍，则圆材埋在墙壁内部的截面面积是（ ）
A. B. C. D.
【答案】D
【解析】
【分析】利用扇形面积公式和三角形面积公式即可.
【详解】由题意得劣弧的长为2，半径，
设，则，即，
则扇形的面积为，
过点作，则，则，，
，则，
所以圆材埋在墙壁内部的截面面积等于，
故选：D.
8. 设函数是定义在上的奇函数，对任意，都有，且当时，
，若函数（且）在上恰有4个不同的零点，则实数的取值范围是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】分析可知，函数的周期为4，作出函数的图像，依题意可得数与的图像在上有4个不同的交点，然后分及讨论即可．
【详解】解：函数是定义在上的奇函数，当时，，
当时，，所以，
即当时，
又对任意，都有，则关于对称，且，
，即函数的周期为，
又由函数且在上恰有个不同的零点，
得函数与的图像在上有个不同的交点，又，
当时，由图可得，解得；
当时，由图可得，解得．
综上可得.
故选：C．
二、多项选择题（本大题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分）
9. 已知，则下列等式正确的是（ ）
A. B.
C. D.
【答案】ABD
【解析】
【分析】运用指数幂运算公式及对数运算公式计算即可.
【详解】对于A项，因为（，），所以，即，故A项正确；
对于B项，由A项知，所以，故B项正确；
对于C项，由A项知，所以，又，所以不一定成立，故C项不成立；
对于D项，由A项知，所以，故D项正确.
故选：ABD.
10. 下列不等式成立的是（ ）
A. B.
C. D.
【答案】BD
【解析】
【分析】结合正弦函数、余弦函数在各个区间的单调性判断.
【详解】因为，且函数在上单调递增，则，故选项A错误；
因为，且函数在上单调递减，则，即，故选项B正确；
因为，且函数在上单调递减，则，故选项C错误；
因为，且函数在上单调递减，则，故选项D正确；
故选：BD
11. 关于函数的下述四个结论，正确的有（ ）
A. 若，则
B. 的图象关于点对称
C. 函数在上单调递增
D. ）的图象向右平移个单位长度后所得的图象关于y轴对称
【答案】ABD
【解析】
【分析】①根据对称中心进行分析；②根据对称中心对应的函数值特征进行分析；③根据的单调性进行分析；④利用函数图象的平移进行分析，注意诱导公式的运用．
【详解】由知点，是图象的两个对称中心，则
，A正确；
因为，所以点是的对称中心，B正确；
由，解得，
当时，在上单调递增，则在上单调递增，在上单调递减，C错误；
的图象向右平移个单位长度后所得图象对应的函数为
，是偶函数，所以图象关于y轴对称，D正确，
故选：ABD．
三、填空题（本大题共3小题，每小题5分，共15分）
12. 已知函数，则的值为__________．
【答案】4
【解析】
【分析】运用代入法，结合对数的运算性质进行求解即可.
【详解】由题意可得，，所以．
故答案为：4
13. 函数在的值域________．
【答案】
【解析】
【分析】化简函数，令，结合的单调性求解．
【详解】
，
∵，
∴，
令，
则在递增，在递减，
当时，y取最小值1，
当时，y取最大值，
故函数的值域是，
故答案为：．
14. 已知函数，若不等式对恒成立，则实数a的取值范围是_______．
【答案】
【解析】
【分析】判断函数的单调性，利用其解析式推出，则可将不等式对恒成立，转化为，即对恒成立，即可求得答案.
【详解】由题意知单调递增，故在R上单调递增，
又，
故不等式对恒成立，
即对恒成立，
所以，即对恒成立，
当时，，
故，即实数a的取值范围是，
故答案为：
【点睛】本题考查了函数不等式恒成立求解参数范围问题，解答时要注意判断函数的单调性以及函数满足的性质，因而解答的关键是利用函数满足的性质脱去函数符号“f”,将问题转化为，即对恒成立，即可解决.
四、解答题（本大题共5小题，共77分，解答应写出必要的文字说明、证明过程及验算步骤）
15. （1）已知，求.
（2）已知，，求.
【答案】（1）；（2）.
【解析】
【分析】
（1）将原式化为即可求出；
（2）由平方可得，即可求出.
【详解】（1）∵，
原式.
（2）∵，∴，∴.
.
∵，∴，∴.
16. 函数的部分图像如图所示.
（1）求及图中的值，并求函数的最小正周期；
（2）若在区间上只有一个最小值点，求实数的取值范围.
【答案】（1），，最小正周期为2
（2）
【解析】
【分析】（1）将代入解出，进而求解即可；
（2）由余弦函数图像和性质求解即可.
【小问1详解】
将代入得，解得，
所以，
令得，，解得，，
所以图中对称轴为，
由对称性得，解得.
的最小正周期.
【小问2详解】
由余弦函数的性质令解得，，
由余弦函数的图像在区间上只有一个最小值点，则，
即实数的取值范围为.
17. 已知函数是奇函数.
（1）求实数的值；
（2）判断并用定义法证明函数的单调性：
（3）若，且当时，恒成立，求实数的取值范围.
【答案】（1）；
（2）单调递增，证明见解析；
（3）.
【解析】
【分析】（1）由奇函数的性质可得，即可求参数；
（2）令，作差法判断大小即可；
（3）问题化为时恒成立，由指数、分式性质求的区间值域，即可得参数范围.
【小问1详解】
由题设，
所以，即.
【小问2详解】
单调递增，证明如下：
由（1）知：，
令，则
，而，，，
所以，故单调递增.
【小问3详解】
由题设，当时恒成立，而，
所以即可，故实数的取值范围为.
18. 已知定义在上的函数满足且，.
（1）求的解析式；
（2）若不等式恒成立，求实数取值范围；
（3）设，若对任意的，存在，使得，求实数取值范围.
【答案】（1）
（2）
（3）
【解析】
【分析】（1）根据列方程，求解即可；
（2）根据函数的单调性化简不等式，分离参数，利用基本不等式求最值即可；
（3）由题意得，先根据函数的单调性求得，再求解使得
成立的实数取值范围即可.
【小问1详解】
由题意知，，
即，所以，
故
【小问2详解】
由（1）知，，
所以在上单调递增，
所以不等式恒成立等价于恒成立，
即恒成立
设，则，，当且仅当，即时，等号成立
所以，
故实数的取值范围是
【小问3详解】
因为对任意的，存在，使得，
所以在上的最小值不小于在上的最小值，
因为在上单调递增，
所以当时，，
又的对称轴为，，
当时，在上单调递增，，解得，
所以；
当时，在上单调递减，在上单调递增，
，解得，所以；
当时，在上单调递减，，解得，
所以，
综上可知，实数的取值范围是
【点睛】结论点睛：本题考查不等式的恒成立与有解问题，可按如下规则转化：
一般地，已知函数，，，.
（1）若，，有成立，则；
（2）若，，有成立，则；
（3）若，，有成立，则；
（4）若，，有成立，则的值域是的值域的子集.
19. 列奥纳多达芬奇（Lenard da Vinci，1452-1519）是意大利文艺复兴三杰之一．他曾提出：固定项链的两端，使其在重力的作用下自然下垂，项链所形成的曲线是什么？这就是著名的“悬链线问题”，后人给出了悬链线的函数表达式，其中为悬链线系数，称为双曲余弦函数，其函数表达式为，相反地，双曲正弦函数的函数表达式为．
（1）证明：；
（2）求不等式：的解集；
（3）函数的图象在区间上与轴有2个交点，求实数的取值范围．
【答案】（1）证明见解析；
（2）（
（3）
【解析】
【分析】（1）结合双曲余弦函数和双曲正弦函数代入计算即可；
（2）求出的单调性和奇偶性，得到，，求出解集；
（3）参变分离得到在有2个实数根，换元得到，由对勾函数单调性得到的值域，与有两个交点，故需满足，即.
【小问1详解】
．
【小问2详解】
因为恒成立，故是奇函数．
又因为在上严格递增，在上严格递减，
故是上的严格增函数，
所以，即，
所以，解得，
即所求不等式的解集为；
【小问3详解】
因为的图象在区间上与轴有2个交点，
所以，
即在有2个实数根，
所以在有2个实数根，
令，易知在上单调递增，
所以，
则，
令，，
由对勾函数性质可知，在上单调递减，在上单调递增，
又，作函数草图如图，
当时，函数与有两个交点，
即函数的图象在区间上与轴有2个交点，
所以，即.
【点睛】方法点睛：新定义问题的方法和技巧：
（1）可通过举例子方式，将抽象的定义转化为具体的简单的应用，从而加深对信息的理解；
（2）可用自己的语言转述新信息所表达的内容，如果能清晰描述，那么说明对此信息理解的较为透彻；
（3）发现新信息与所学知识的联系，并从描述中体会信息的本质特征与规律；
（4）如果新信息是课本知识的推广，则要关注此信息与课本中概念的不同之处，以及什么情况下可以使用书上的概念.